Luku 10.2: Hirsiä ja sananmuunnoksia
Tästä sivusta:
Pääkysymyksiä: Mitä korkeamman asteen metodeita merkkijonoilla on? Miten suunnittelen ja toteutan itse merkkijonoja käsittelevän algoritmin? Kaverini väittää olevansa hyvä hirsipuupelissä; miten saan hänelle jauhot suuhun?
Mitä käsitellään? Lisäharjoitusta muun muassa algoritmin toteuttamisesta, merkkijonoista, hakurakenteista ja korkeamman asteen metodeista.
Mitä tehdään? Ohjelmoidaan, kunhan tajutaan ensin, mitä on tarkoitus ohjelmoida. Luku muodostuu pääosin yhdestä tehtävästä; lopussa on vapaaehtoista lisätekemistä.
Suuntaa antava työläysarvio:? Koodirivejä ei välttämättä paljonkaan tarvita, mutta aiheeseen perehtyminen, ratkaisumallin keksiminen, koodirivien muotoilu ja ohjelman testaus kyllä yhteensä vievät aikaa. Viisi tuntia? Älä jää tehtävään jumiin, vaan pyydä apua ajoissa. Myös lopun vapaaehtoiseen osaan menee helposti tunteja.
Pistearvo: C90.
Oheismoduulit: Peeveli (uusi). Vapaaehtoisessa lisätehtävässä Sananmuunnos (uusi).

Pohjustus tuleviin tehtäviin: lisää merkkijonoista
Kertaus
Seuraavat taustatiedot lienet jo oppinut. Kertaa yksityiskohtia edellisistä luvuista ja Scalaa kootusti -sivulta tarvittaessa.
Alkiokokoelmilla kuten puskureilla ja vektoreilla on monenlaisia ensimmäisen asteen metodeita (esim.
take,contains,indexOf; luku 4.2) ja korkeamman asteen metodeita (esim.filter,map,maxBy; luvut 6.3, 7.1 ja 10.1).Merkkijonot koostuvat
Char-tyyppisistä arvoista, joista kukin edustaa yhtä merkkiä (luku 5.2).Merkkijonoilla on monia nimenomaisesti merkkijonojen käsittelyyn liittyviä metodeita (esim.
trim,toUpperCase; luku 5.2).Merkkijonot ovat olioita; ne ovat merkeistä koostuvia alkiokokoelmia (luku 5.2). Kuten muitakin kokoelmia, niitä voi esimerkiksi käydä läpi
for-silmukalla (luku 5.6).Merkkijonoilla on myös monia vastaavia ensimmäisen asteen metodeita kuin muillakin alkiokokoelmilla (esim.
take,contains,indexOf; luku 5.2).
Koskapa merkkijonotkin ovat alkiokokoelmia, tutut korkeamman asteen kokoelmankäsittelymetoditkin on määritelty myös niille.
Muutama esimerkki String-olioiden korkeamman asteen metodeista
Kokeillaan ensin vaikkapa foreach-metodia ja tulostetaan kukin merkkijonon alkio eli
merkki:
"Oi!".foreach(println)O i !
Suodattakaamme filter-metodilla merkkijonosta kaikki paitsi pienet kirjaimet. Apuna
käytämme Char-olion metodia isLower, joka kertoo, onko kyse pienestä kirjoitusmerkistä:
"Oi, maamme Suomi!".filter( _.isLower )res0: String = imaammeuomi
sorted-metodi järjestää merkit niiden luonnolliseen järjestykseen (luku 10.1) eli
Unicode-merkistön mukaan:
"Oi, maamme Suomi!".sortedres1: String = " !,OSaaeiimmmmou"
sortBy-metodilla voi järjestää merkit vaikkapa pieneksi muutettujen versioiden
mukaan:
"Oi, maamme Suomi!".sortBy( _.toLower )res2: String = " !,aaeiimmmmOoSu"
Char-oliolta voi pyytää pienen version toLower-metodilla.
Huomaa ero tämän ja edellisen esimerkin paluuarvoissa.
map-metodi muodostaa paluuarvonsa soveltamalla parametrifunktiota kuhunkin
merkkijonon merkkiin. Tässä pari esimerkkiä:
"Suomi on oiva maa.".map( merkki => if merkki.isLower then merkki.toUpper else merkki.toLower )res3: String = sUOMI ON OIVA MAA. "Oi!".map( _.isLower )res4: IndexedSeq[Boolean] = Vector(false, true, false)
Peeveli-peli
Taustaa: hirsipuupeli

A, I ja N ovat osuneet. Viisi arvausta ovat olleet huteja, joten on piirretty tikku-ukon pää, vartalo, kädet ja toinen jalka. Seuraavasta hutista piirretään toinenkin jalka, ja arvaaja häviää.
Hirsipuu on sanapeliklassikko, jossa yksi pelaaja valitsee perusmuotoisen sanan ja toinen yrittää kirjain kerrallaan arvata, mistä sanasta on kyse. Sanan pituus on molempien pelaajien tiedossa. Arvaajan valitessa kirjaimen arvuuttajan on paljastettava kaikki ne kohdat, joissa kyseinen kirjain esiintyy piilosanassa. Jos arvaus ei paljasta yhtään uutta kirjainta piilosanasta, piirtää arvuuttaja yhden viivan lisää hirsipuukuvaan.
Jos kuva tulee muutaman "hutin" seurauksena valmiiksi, arvaaja häviää. Arvaaja voittaa, jos hän saa paljastettua koko sanan.
Voit lukea hirsipuupelistä lisää esimerkiksi Wikipediasta.
Joillekin pelistä varmaankin tulee mieleen joulukuussa 2021 viraalisuosioon noussut
Wordle <https://en.wikipedia.org/wiki/Wordle>_, joka on eräänlainen hirsipuupelin
ja Mastermindin sekoitus.
Pelistä on monia tietokoneversioita, joissa tietokone arvuuttaa pelaajalta sanoja. Samoin kuin ihmisten välinenkin hirsipuupeli, nämä perinteiset versiot perustuvat siihen, että arvaaja voi luottaa arvuuttajaan.
Nyt ohjelmoidaan hieman toisenlainen peli. Arvuuttajaksi on päästetty Peeveli, ja se ei pelaa reilua peliä.
Hirsipuussa huijaaminen
Tavallisessa hirsipuupelissä arvuuttajana toimiva pelaaja valitsee arvattavan sanan heti pelin aluksi ja tunnollisesti paljastaa siinä esiintyviä kirjaimia arvausten kertyessä. Mutta mitä jos hän ei tekisikään niin?
Kuvitellaan tilanne. Peli on juuri alkanut, olet arvaajan roolissa ja arvuuttaja on tietämättäsi valinnut sanan KAIVAA. Piilosana näyttää siis tältä:
_ _ _ _ _ _
Jos arvaat kirjaimen A, arvuuttajan pitäisi paljastaa kolme A-kirjainta. Mutta hän voikin tietämättäsi vaihtaa aiemmin valitsemansa piilosanan A:ttomaksi sanaksi KOLMIO ja ilmoittaa, ettei A-kirjaimia löytynyt.
Kuvitellaan toinen tilanne. Olet saanut arvattua kaikki paitsi yhden kirjaimen seuraavasta viisikirjaimisesta piilosanasta, mutta sinulla on vain yksi arvaus jäljellä:
_ O I M I
Oletetaan vielä, että kirjaimet T ja L ovat arvaamatta. Koska haetaan perusmuotoista sanaa, niin suomen kielessä on vain kaksi mahdollista ratkaisua: TOIMI ja LOIMI. Kuitenkin jos arvaat T, arvuuttaja voi väittää ajatelleensa sanaa LOIMI — ja toisinpäin. Et voi voittaa petkuttavaa arvuuttajaa vastaan!
Peevelin perusidea
Peeveli-pelissä tietokone toimii arvuuttajana ja ihminen arvaajana. Tietokone kuitenkin huijaa järjestelmällisesti ja tarjoaa näin selvästi kovemman vastuksen. Apuna se käyttää laajaa sanaluetteloa sekä kieroa algoritmia: tietokone ei valitse piilosanaa aluksi lainkaan, vaan pitää salaa kirjaa kaikista niistä sanoista, jotka ovat edelleen mahdollisia ratkaisuja pelaajan tekemien arvausten ja aiemmin paljastettujen kirjainten puitteissa. Aina pelaajan arvatessa Peeveli pyrkii pitämään jäljelle jäävien ratkaisuvaihtoehtojen määrän suurena valitessaan, mitä (jos mitään) kirjaimia piilosanasta paljastetaan.
Kuvittele itsesi arvuuttajan asemaan. Olkoon piilosanan pituudeksi valittu neljä kirjainta. Kuvitellaan lisäksi, että suomen kielessä ei ole mitään muita nelikirjaimisia sanoja kuin seuraavat kymmenen. Piilosanan on siis oltava jokin niistä:
AAVA AIKA AIVO ALLI KULU RIMA RÄKÄ SOLA SUMU TAAS
Vastustajasi arvaa aluksi kirjaimen A. Mitä kannattaa tehdä?
Katsotaan ensin, miten A:t sijoittuvat tunnettuihin nelikirjaimisiin sanoihin:
AAVA AIKA AIVO ALLI KULU RIMA RÄKÄ SOLA SUMU TAAS
Sanat jakautuvat muutamaan ryhmään sen perusteella, miten A-kirjaimet niihin sijoittuvat:
Ryhmä |
Selitys |
Sanat |
|---|---|---|
|
Alussa kaksi, lopussa yksi A. |
AAVA |
|
Alussa ja lopussa yksi A. |
AIKA |
|
Keskellä kaksi A:ta. |
TAAS |
|
Alussa yksi A. |
AIVO, ALLI |
|
Lopussa yksi A. |
RIMA, SOLA |
|
Ei A-kirjaimia. |
KULU, RÄKÄ, SUMU |
Sinulla on siis kuusi vaihtoehtoa, joista on poimittava yksi. Perushyvä tapa on valita ryhmistä suurin. Tässä tapauksessa se on viimeinen ryhmä. Siispä ilmoitat vastustajallesi, että sanassa ei ole A-kirjaimia ja pidät mielessä, että mahdollisia ratkaisuja on vielä kolme: KULU, RÄKÄ ja SUMU.
Jos sanalistassa olisi ollut myös A:lla alkavat sanat ANTI ja AUVO, niin ryhmä A___
olisi ollut suurin. Tällöin olisit paljastanut vastustajalle A-kirjaimen sanan alusta ja
jäänyt odottamaan seuraavia arvauksia sanavalikoimalla AIVO, ALLI, ANTI ja AUVO.
Oletetaan nyt, että olet valinnut ryhmän, jossa ovat KULU, RÄKÄ ja SUMU. Vastustajasi
arvaa seuraavaksi kirjaimen U. Muodostuvat ryhmät _U_U (jossa KULU, SUMU) ja
____ (jossa RÄKÄ). Ensinmainittu on suurempi, joten paljastat vastustajalle
U-kirjaimet sanan toisella ja viimeisellä paikalla.
Kun vastustaja arvaa kirjaimen, joka ei esiinny missään mahdollisista ratkaisusanoista, ei muodostu kuin yksi sanaryhmä, jossa ovat kaikki jäljellä olevat sanat. Tällöin valitset tietysti tämän ainoan ryhmän.
Joskus käy niin, että yhtä suuria suurimpia sanaryhmiä on useita. Tällöin voit valita jonkin mielivaltaisen ryhmän tai vaikkapa sen ryhmistä, joka paljastaa vastustajalle vähiten kirjaimia.
Peeveli-moduuli
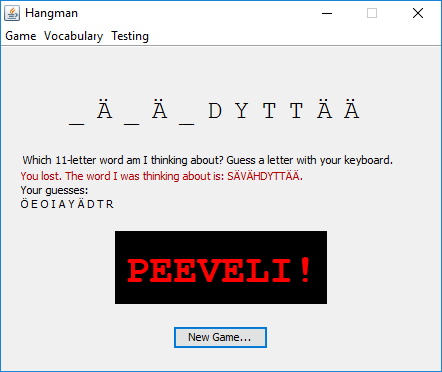
Peeveli-peli ei piirrä hirsipuuta vaan käyttää punaisia kirjaimia hutien laskemiseen. Kirjaimet ilmestyvät, kun pelaajalla on enää niukasti vastausyrityksiä jäljellä.
Oheismoduulissa Peeveli on osin toimiva toteutus yllä kuvatulle pelille. Pelin käyttöliittymä on annettu valmiina, mutta toimintalogiikassa on pahoja puutteita.
Tehtävänanto
Kokeile pelata annettua versiota pelistä. Käynnistysolio on
o1.peeveli.gui.PeeveliApp. Huomaat muun muassa, että:Peli on todella lepsu eikä toimi ollenkaan niin kuin pitäisi. Se hyväksyy kaikki arvaukset ja paljastaa aina yhden seuraavan kirjaimen sanasta.
Peli ei lopu silloinkaan, kun pitäisi.
Voit vaihtaa sanastoa valikosta.
Voit myös panna päälle testaukseen sopivan tilan, jossa Peeveli tulostelee tekstikonsoliin kaikki jäljellä olevat vaihtoehdot (jotka annettu versio pelistä tosin säyseästi karsii suoraan yhteen).
Tutustu moduulin Scaladoc-dokumentaatioon ja ohjelmakoodiin.
Toteuta ohjelmakoodista puuttuvat osat, jotka saavat Peevelin toimimaan yhtä viekkaasti kuin yllä on kuvattu.
Tarkennus
Yllä Peeveli-algoritmin kuvauksen lopussa mainittiin, että sanaryhmien ollessa yhtä suuret voi olla hyvä ajatus valita se ryhmä, joka paljastaa vastustajalle vähiten kirjaimia. Tuo on tässä tehtävässä vapaaehtoista. Toteuta se lisäpiruilu vain, jos haluat lisähaastetta tehtävään. Riittää mainiosti, että poimit tasatilanteessa suurimpien joukosta mielivaltaisen ryhmän.
Ohjeita ja vinkkejä
Kaikki tarvittavat muutokset tulevat tiedostoon
GameState.scala.Yksityinen metodi
revealkannattaa toteuttaa ja ottaa avuksiguessLetter-metodin toteutuksessa.Muista literaaleja käyttäessäsi, että
String-literaalit kuten"jono"ovat lainausmerkeissä muttaChar-literaalit kuten'm'kirjoitetaan heittomerkkeihin.groupBy(luku 10.1)
A+ esittää tässä kohdassa tehtävän palautuslomakkeen.
Lisäharjoitusta: Sananmuunnos-moduuli
Kuten Sananmuunnos-moduulin scaladocit kertovat, projektissa tulisi olla luokka
Sana, jota voi käyttää esimerkiksi tähän tapaan:
val eka = Sana("prätkä")eka: o1.sananmuunnos.Sana = pr|ä|tkä
val toka = Sana("kontti")toka: o1.sananmuunnos.Sana = k|o|ntti
eka.muunnos(toka)res5: String = kotka präntti
Sana("pastori").muunnos(Sana("Luttinen"))res6: String = lustori pattinen
Sana-luokan käyttöä kätevöittämässä on myös tarkoitus olla kumppaniolio, jolla
on kaksiparametrinen muunnos-metodi. Näin muuntaessa ei tarvitse erikseen luoda
Sana-olioita:
Sana.muunnos("pastori", "Luttinen")res7: String = lustori pattinen
Luokka Sana kumppaniolioineen puuttuu.
Tehtävänanto
Tutustu perusteellisesti moduulin scaladoceihin. Niistä löydät lisäesimerkkejä
sekä tarkennuksia siihen, miten Sana-luokan tulisi toimia.
Toteuta luokka Sana ja sen kumppaniolio.
Pakkauksen o1.sananmuunnos funktioista
Pakkaus o1.sananmuunnos sisältää valmiina annettuja funktioita, jotka liittyvät
eräisiin suomen kielen piirteisiin ja joista on apua Sana-luokan toteuttamisessa.
Niiden avulla voit esimerkiksi tutkia millaisia äänteitä kirjoitusmerkit vastaavat:
onKonsonantti('t')res8: Boolean = true
onKonsonantti('a')res9: Boolean = false
onKonsonantti('T')res10: Boolean = true
onKonsonantti('!')res11: Boolean = false
onVokaali('a')res12: Boolean = true
Voit myös muuttaa takavokaalin etuvokaaliksi tai toisin päin:
eteen('a')res13: Char = ä
taakse('ä')res14: Char = a
Pakkauksessa on myös muita funktioita kuin yllä esitellyt. Lisätietoja löytyy scaladoceista.
Ohjeita ja vinkkejä
Toteutustapa on vapaa, mutta käytä erilaisia merkkijonojen metodeita. Kaikkia hyödyllisiä metodeita ei ole käsitelty tässä luvussa. Kertaa käytettävissä olevia metodeita luvuista 5.2 ja 6.3. tai Scalaa kootusti -sivulta.
Hyödynnä myös
o1.sananmuunnos-pakkauksen funktioita. Et tarvitse niistä kaikkia; se, mitä tarvitset, riippuu valitsemastasi toteutustavasta. Löydät funktioiden Scaladoc-dokumentaation klikkaamalla pakkauksen nimeä Scaladoc-sivun vasemman reunan valikossa.Sana-luokalla on kaksi julkista metodia:muunnosjatoString. Aloita toteuttamallatoString: se edellyttää sanojen jakamista osiin, mikä on esivaihe varsinaiselle sananmuunnosten muodostamiselle.Yksityisten apumetodien määritteleminen
Sana-luokkaan on sallittua ja suotavaa. Vältä saman tai samankaltaisen koodin kirjoittamista useammin kuin kerran.Voit olettaa, että kaikki syötteeksi annetut sanat ovat suomea eivätkä sisällä numeroita eivätkä mitään välimerkkejä tai erikoismerkkejä.
Huomaa kuitenkin, että
Sana-luokan on tulkittava saamassaan syötteessä mahdollisesti esiintyvät isot kirjaimet pieniksi.Voit olettaa, ettei ohjelmalle anneta syötteeksi yhdyssanoja eikä sellaisia sanoja, joissa vokaalisointu ei päde. Esimerkiksi "vampyyri"- ja "anonyymi"-tyyppisiä sanoja ei tarvitse erikseen huomioida.
"Oikean elämän sananmuunnoksiin" liittyy muitakin sääntöjä kuin dokumentaatiossa kuvatut. Niistä ei kuitenkaan pidä välittää. Toteuta vain ne asiat, jotka on pyydetty.
A+ esittää tässä kohdassa tehtävän palautuslomakkeen.
Lisäluettavaa: metodilaajennukset
Voiko kirjastoluokkaan lisätä omia metodeita? Voiko Scalaan lisätä operaattoreita?
Kirjaston täydentämisessä voi joissakin tapauksissa hyödyntää periytymistä: laaditaan kirjastoluokalle aliluokka, johon lisätään haluttu metodi. Tuosta omasta aliluokasta voi sitten luoda ilmentymiä.
Periytyminen ei kuitenkaan aina sovi ratkaisuksi. Ensinnäkin
monet kirjastoluokat on määritelty final-määreellä, joka estää
niistä perimisen (esim. tehokkuus- tai muista laatusyistä). Toiseksi:
mitä jos haluamme laatia uusia metodeita, joita voisi kutsua
mille tahansa tietyn kirjastoluokan oliolle, vaikka noita metodeita
ei tuossa kirjastossa ole määritelty lainkaan?
Saattaa kuulostaa mahdottomalta. Ja tosiaan: jos et muokkaa kirjaston koodia, et suoranaisesti voi lisätä kirjastoluokkiin metodeita.
Mutta mahdotonkin on tavallaan mahdollista. Ratkaisu löytyy alta.
Metodilaajennus
Tarkastellaan esimerkkiä. Olemme tottuneet käyttämään Double-tyyppiä
Scalan peruskirjastosta. Sillä on omat operaattorinsa mm. yhteen- ja
vähennyslaskuun mutta ei esimerkiksi potenssiin korottamiseen.
Potenssiin korottaminenhan onnistuu kyllä scala.math-pakkauksen
pow-funktiolla.
import scala.math.powpow(2.1, 3.3)res15: Double = 11.569741950241465
Opiskelijat ovat joskus kaipailleet Double-oliolle neliöimismetodia
ja potenssiinkorotusoperaattoria. Vaikka varsinainen lisäys esimerkiksi
Double-luokkaan ei onnistu, saamme Scalan käyttäytymään ikään kuin
olisimme lisänneet siihen omia metodeita.
Määritellään neliö Double-tyypin metodilaajennukseksi (extension
method):
extension (luku: Double) def neliö = pow(luku, 2)def neliö(luku: Double): Double
extension-sanan avulla määritellään, että
laajennamme tietyn tyypin metodivalikoimaa
yhdellä tai useammalla metodilla.
Tässä tapauksessa kyseessä on Double-tyyppi.
Sulkeet ovat pakolliset.
Kun näin on määritelty, luku viittaa jäljempänä
siihen Double-tyyppiseen arvoon, jonka metodista
on kyse. Voit ajatella, että luku on seuraavissa
metodimäärittelyissä samankaltaisessa roolissa kuin
this tavallisissa metodeissa.
Luokkamme tarjoaa metodin neliö, jonka haluamme
"lisätä Double-luokkaan".
Nyt voimme käyttää esimerkiksi neliö-metodiamme ihan tavallisille
lukuarvoille:
5.3.neliöres16: Double = 28.09
Scala-kääntäjä toteaa: Tässä kutsutaan neliö-metodia, jota
Double-oliolla ei ole. Mutta Double-tyypille on olemassa tuon
niminen metodilaajennus. Joten kutsutaan kyseiselle Doublelle
5.3 tuota neliötä.
(Jos laajennus olisi eri pakkauksessa, se pitäisi importata.)
Jatketaan esimerkkiämme ja lisätään potenssiinkorotusoperaattori.
Operaattorit ovat Scalassa metodeita (luku 5.2). Voimme määritellä
operaattorin — vaikkapa ** — samaan syssyyn neliömetodin kanssa:
extension (luku: Double) def neliö = pow(luku, 2) def **(eksponentti: Double) = pow(luku, eksponentti)def neliö(luku: Double): Double def **(luku: Double)(eksponentti: Double): Double
Operaattoriamme voi käyttää joko piste- tai operaattorinotaatiolla:
10.**(5)res17: Double = 100000.0 10 ** 5res18: Double = 100000.0
Kaikki siis sujuu aivan kuin metodi neliö ja "potenssiinkorotusoperaattori"
** olisivat Double-luokassa. Melkoinen taikatemppu!
infix-määre ja @targetName
Edellä määrittelimme metodin, jota suunnittelimme käytettävän
operaattorinotaatiolla: 10 ** 5. Kun tällaisen "operaattorimetodin"
Scalalla määrittelee, on koodiin hyvä lisätä eräs merkintä:
extension (luku: Double)
infix def **(eksponentti: Double) = pow(luku, eksponentti)
Sana infix kirjaa koodiin, että metodi on
tarkoitettu käytettäväksi operaattorinotaatiolla
(jota sanotaan myös infix-notaatioksi).
Tuon määreen saisi jättää poiskin, kun kyseessä on symboleista
koostuva nimi kuten **, mutta asian kirjaaminen nimenomaisesti
koodiin on ihan hyvä tapa. Jos nimi ei olisi symbolinen ja infix
puuttuisi, varoittaisi Scala-kääntäjä operaattorinotaation käytöstä.
Ja kun nyt metodimme nimi koostuu tavallisten kirjoitusmerkkien sijaan symboleista, on hyvä lisätä toinenkin merkintä:
import scala.annotation.targetName
extension (luku: Double)
@targetName("potenssiin")
infix def **(eksponentti: Double) = pow(luku, eksponentti)
@targetName-merkintä liittää metodiin
sanallisen nimen, jota Scala-kääntäjä
sisäisesti käyttää. Tästä on tiettyä
teknistä apua,
ja voi se auttaa metodista puhumisessakin.
Tässä esimerkissämme oli kyseessä metodilaajennus (extension),
mutta infix ja targetName ovat vastaavasti suositeltavia myös
tavallisissa metodeissa, jotka ovat "operaattorimaisia".
Lisätehtävä: sananmuunnosoperaattori
Temppuillaan vielä vähän. Määrittele merkkijonoille sananmuunnosoperaattori. Käytännössä ikään kuin lisäät sananmuunnokset Scala-kieleen:
"lapio" <-> "kontti"res19: String = kopio lantti
Toteuta metodilaajennus, joka mahdollistaa tämän. Tee se
tiedostoon Sana.scala.
Tyyppiluokat
Edellä esiteltiin metodilaajennukset vaihtoehtona periytymiselle, kun haluamme liittää uusia toimintoja olemassa olevaan tietotyyppiin.
Metodilaajennuksia vieläkin voimallisempi tekniikka tunnetaan nimellä tyyppiluokka eli type class. Kiinnostuneet voivat lukea niistä lisää verkosta tai kirjoista.
Palaute
Huomaathan, että tämä on henkilökohtainen osio! Vaikka olisit tehnyt lukuun liittyvät tehtävät parin kanssa, täytä palautelomake itse.
Tekijät
Tämän oppimateriaalin kehitystyössä on käytetty apuna tuhansilta opiskelijoilta kerättyä palautetta. Kiitos!
Materiaalin luvut tehtävineen ja viikkokoosteineen on laatinut Juha Sorva.
Liitesivut (sanasto, Scala-kooste, usein kysytyt kysymykset jne.) on kirjoittanut Juha Sorva sikäli kuin sivulla ei ole toisin mainittu.
Tehtävien automaattisen arvioinnin ovat toteuttaneet: (aakkosjärjestyksessä) Riku Autio, Nikolas Drosdek, Kaisa Ek, Joonatan Honkamaa, Antti Immonen, Jaakko Kantojärvi, Niklas Kröger, Kalle Laitinen, Teemu Lehtinen, Mikael Lenander, Ilona Ma, Jaakko Nakaza, Strasdosky Otewa, Timi Seppälä, Teemu Sirkiä, Anna Valldeoriola Cardó ja Aleksi Vartiainen.
Lukujen alkuja koristavat kuvat ja muut vastaavat kuvituskuvat on piirtänyt Christina Lassheikki.
Yksityiskohtaiset animaatiot Scala-ohjelmien suorituksen vaiheista suunnittelivat Juha Sorva ja Teemu Sirkiä. Teemu Sirkiä ja Riku Autio toteuttivat ne apunaan Teemun aiemmin rakentamat työkalut Jsvee ja Kelmu.
Muut diagrammit ja materiaaliin upotetut vuorovaikutteiset esitykset laati Juha Sorva.
O1Library-ohjelmakirjaston ovat kehittäneet Aleksi Lukkarinen ja Juha Sorva. Useat sen keskeisistä osista tukeutuvat Aleksin SMCL-kirjastoon.
Tapa, jolla käytämme O1Libraryn työkaluja (kuten Pic) yksinkertaiseen graafiseen
ohjelmointiin, on saanut vaikutteita tekijöiden Flatt, Felleisen, Findler ja Krishnamurthi
oppikirjasta How to Design Programs sekä Stephen Blochin oppikirjasta Picturing Programs.
Oppimisalusta A+ luotiin alun perin Aallon LeTech-tutkimusryhmässä pitkälti opiskelijavoimin. Nykyään tätä avoimen lähdekoodin projektia kehittää Tietotekniikan laitoksen opetusteknologiatiimi ja tarjoaa palveluna laitoksen IT-tuki. Pääkehittäjänä on nyt Markku Riekkinen, jonka lisäksi A+:aa ovat kehittäneet kymmenet Aallon opiskelijat ja muut.
A+ Courses -lisäosa, joka tukee A+:aa ja O1-kurssia IntelliJ-ohjelmointiympäristössä, on toinen avoin projekti. Sen suunnitteluun ja toteutukseen on osallistunut useita opiskelijoita yhteistyössä O1-kurssin opettajien kanssa.
Kurssin tämänhetkinen henkilökunta löytyy luvusta 1.1.
Lisäkiitokset tähän lukuun
Peevelin pohjana on käytetty Keith Schwarzin ideoimaa tehtävää.
Isoja kirjaimia kuvaavat aakkoset ovat tässä merkistössä ennen pieniä kirjaimia.