Luku 2.5: Kuvia ja kuvauksia
Tästä sivusta:
Pääkysymyksiä: Saisiko lisää luokkia? Käsiteltäisiinkö kuvia hieman monipuolisemmin? Miten kätevöitän olioiden testaamista REPLissä?
Mitä käsitellään? Metodeita, jotka luovat ja palauttavat
ilmentymiä; metodeita, jotka vastaanottavat viittauksia
olioihin. toString-metodi. Kuvien asemointia, rajaamista yms.
Mitä tehdään? Useita ohjelmointitehtäviä tekstin lomassa.
Suuntaa antava työläysarvio:? Pari tuntia ilman lisätehtäviä? Uutta käsitteistöä on hädin tuskin lainkaan. Ohjelmointirutiinin puuttuessa tehtävät voivat silti takelluttaa.
Pistearvo: A50.
Oheismoduulit: Odds. Lopussa palataan taas lyhyesti Aliohjelmia-moduuliin.

Tavoite: sijainteja kuvissa
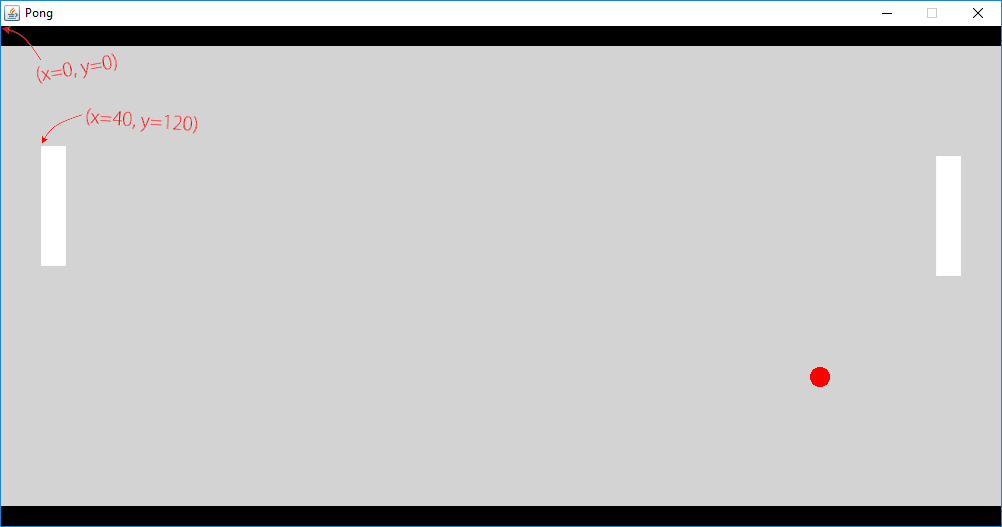
Pong-pelin mailan kulma on koordinaateissa (40,120), kun lasketaan pikseleinä koko kuvan vasemmasta yläkulmasta. Graafisessa ohjelmoinnissa käytetään usein koordinaatteja, jotka kasvavat vasemmalta oikealle ja ylhäältä alas.
Monissa ohjelmissa on käyttöä kaksiulotteisille koordinaateille. Koordinaattiparilla voimme mallintaa vaikkapa pelihahmon sijaintia pelissä. Grafiikkaa käsitellessä taas voimme ilmaista koordinaateilla tietyn kuvapisteen sijainnin, johon haluamme kohdistaa toimenpiteen:
"Rajaa isosta kuvasta 400 pikseliä leveä ja korkea pala, jonka vasen yläkulma on 150 pikseliä vasemmasta reunasta ja 200 pikseliä yläreunasta."
"Piirrä pieni kuva ison kuvan päälle niin, että pienen kuvan keskipiste on ison kuvan kohdassa (300,200) olevan pikselin päällä."
"Piirrä piste pikselikoordinaatteihin (x,y), missä x ja y kertovat hiiren kursorin tämänhetkisen sijainnin näkymän vasemmasta yläkulmasta lukien."
Opit pian juuri tuontapaisia käskyjä. Ensin kehitämme käyttöömme tarvittavan
koordinaatteja kuvaavan luokan ja siinä ohessa parantelemme viime luvun Odds-ohjelmaa.
Sijaintiluokka Pos
Koordinaattipareja kuvaavan luokkamme nimeksi tulkoon ytimekkäästi Pos englannin sanan
position mukaan. Jos sitä voisi käyttää vaikka näin?
val eka = Pos(50, 12.5)eka: Pos = Pos@3245f574 val toka = Pos(-30, 100)toka: Pos = Pos@2fcad1a3 eka.xres0: Double = 50.0 eka.yres1: Double = 12.5 eka.descriptionres2: String = (50.0,12.5) toka.descriptionres3: String = (-30.0,100.0)
Tuo on opituilla keinoilla suoraviivaista toteuttaa luokaksi:
class Pos(val x: Double, val y: Double):
def description = "(" + this.x + "," + this.y + ")"
Toki koordinaatteja voisi kuvata ohjelmassa Double-arvoilla ilman Pos-luokkaakin.
Jotain sellaistahan vähän teimmekin luvuissa 1.7 ja 1.8, kun laskimme pisteiden välisiä
etäisyyksiä. Mutta kuten tulee osoittautumaan, on edullista määritellä sijainnin
käsitettä mallintamaan oma tietotyyppi, joka kytkee yhteen kaksi arvoa (x ja y) ja
tarjoaa valikoiman metodeita tällaisten koordinaattiparien käsittelyyn.
Jos kokeilet Posia REPLissä...
... jätä oheinen class-määrittely kirjoittamatta sinne. Tämän
luvun esittelemää Pos-luokkaa vastaava toteutus on jo valmiina
o1-pakkauksessa ja automaattisesti käytössäsi REPLissä.
Sillä on myös muita ominaisuuksia kuin yllä kuvatut perustoiminnot.
Uusia ilmentymiä metodilla
Sijainneilla laskeminen
Sijainneilla voi laskea synnyttäen uusia sijainteja. Voidaan esimerkiksi määrittää sijainti, joka on tietyn matkan päässä "oikealle" jostakin toisesta sijainnista.
val vasenYlakulma = Pos(40, 120)vasenYlakulma: Pos = Pos@2c8d4d39 val vahanOikealle = vasenYlakulma.addX(30)vahanOikealle: Pos = Pos@25b7325c
Huomaa: addX-metodi palautti viittauksen uuteen Pos-olioon, joka kuvaa sijaintia
jonka x-koordinaatti on 30 yksikköä (esim. pikseliä) suurempi kuin metodikutsun
kohdeoliolla. Tuolle uudelle oliolle, johon muuttuja vahanOikealle nyt viittaa, voi
kutsua mitä vain Pos-olioiden metodia:
vahanOikealle.descriptionres4: String = (70.0,120.0) val enemmanOikealle = vahanOikealle.addX(70)enemmanOikealle: Pos = Pos@2d9ff490 enemmanOikealle.descriptionres5: String = (140.0,120.0)
Metodin addX voi toteuttaa näin:
class Pos(val x: Double, val y: Double):
def description = "(" + this.x + "," + this.y + ")"
def addX(dx: Double) =
val relativePosition = Pos(this.x + dx, this.y)
relativePosition
end Pos
Lasketaan uudet koordinaatit this-olion tietojen ja
parametrimuuttujan dx ilmaiseman etäisyyden perusteella.
X-koordinaatti saadaan summana; y-koordinaatti on sama kuin
alkuperäisellä sijainnilla.
Palautetaan viittaus luotuun olioon.
Äskeisessä versiossa käytettiin paikallista muuttujaa relativePosition vain välivaiheen
korostamiseksi: ensin luodaan olio, sitten palautetaan viittaus. Lyhyemminkin voimme kyllä
kirjoittaa:
class Pos(val x: Double, val y: Double):
def description = "(" + this.x + "," + this.y + ")"
def addX(dx: Double) = Pos(this.x + dx, this.y)
end Pos
On kutsuvan koodin asia, mitä se tekee metodin palauttamalla viittauksella. Ylempänä
sijoitimme addX-metodin palauttaman viittauksen muuttujaan (enemmanOikealle),
mutta metodikutsua voi myös käyttää osana isompaa lauseketta. Metodikutsuja voi
esimerkiksi ketjuttaa:
enemmanOikealle.addX(100).descriptionres6: String = (240.0,120.0)
Sijaintiolion metodi addX palauttaa viittauksen
toiseen sijaintiolioon. Tuota toista sijaintia ei panna
mihinkään talteen, vaan sille vain saman tien kutsutaan
description-metodia, joka palauttaa merkkijonon.
Vastaavasti kuin addX voidaan tietysti määritellä metodi addY. Alla on tehty niin;
sieltä löytyy myös metodi add, joka huomioi molemmat koordinaatit.
class Pos(val x: Double, val y: Double):
def description = "(" + this.x + "," + this.y + ")"
def addX(dx: Double) = Pos(this.x + dx, this.y)
def addY(dy: Double) = Pos(this.x, this.y + dy)
def add(dx: Double, dy: Double) = Pos(this.x + dx, this.y + dy)
end Pos
Nyt meillä on hyvä alku Pos-luokalle; lisäämme siihen kohta muitakin metodeita.
Yleisemmällä tasolla voimme todeta, että olemme määritelleet paitsi erään tietotyypin,
myös sääntöjä, jotka määräävät, millaisella logiikalla uusia kyseisen tyyppisiä arvoja
syntyy, kun niillä lasketaan.
Odds-tehtävä (osa 2/9)
Johdanto
Palataan luvussa 2.4 aloittamaamme Odds-ohjelmaan.
Tarkastellaan kahta tapahtumaa, vaikkapa kuutosen heittämistä nopalla (Odds 5/1) ja
klaavan heittämistä kolikolla (Odds 1/1).
val six = Odds(5, 1)six: Odds = o1.odds.Odds@60a6fd val tails = Odds(1, 1)tails: Odds = o1.odds.Odds@111a008
Odds sille, että kuutonen ei toteudu, saadaan kääntämällä luvut toisin päin: 1/5.
Kruunan heittäminen taas on klaavan kanssa yhtä todennäköistä, ja 1/1 onkin molemmin
päin sama.
Yleisemmin: jos Odds-olio kuvaa tapausta a1/a2, niin käänteisen tapahtuman
Odds on a2/a1.
Tehtävänanto
Täydennä Odds-luokkaa vaikutuksettomalla metodilla not, jonka avulla voi muodostaa
käänteistapauksia kuvaavia olioita. Sen pitää toimia näin:
val somethingOtherThanSix = six.notres7: Odds = o1.odds.Odds@56258cb3 somethingOtherThanSix.fractionalres8: String = 1/5 tails.not.fractionalres9: String = 1/1 Odds(10, 19).not.fractionalres10: String = 19/10
Ohjeita ja vinkkejä
not-metodin on siis luotava uusiOdds-olio ja palautettava viittaus siihen. Se ei saa palauttaa pelkkää merkkijonoa, lukua, tms.Huomattavan pieni määrä koodia riittää.
A+ esittää tässä kohdassa tehtävän palautuslomakkeen.
Olioihin viittaavia parametreja
Etäisyysmetodeita pseudokoodina
Tehdään Pos-luokkaamme metodit xDiff ja yDiff, joilla saa laskettua kahden Posin
välisen etäisyyden yhden koordinaattiakselin suunnassa.
val eka = Pos(50, 12.5)eka: Pos = Pos@3245f574 val toka = Pos(-30, 100)toka: Pos = Pos@2fcad1a3 val xKoordinaattienErotus = toka.xDiff(eka)xKoordinaattienErotus: Double = 80.0 toka.yDiff(eka)res11: Double = -87.5 eka.yDiff(toka)res12: Double = 87.5 eka.xDiff(Pos(60, 20))res13: Double = 10.0
Tässä ensimmäinen hahmotelma metodien toteutuksesta. Se ei vielä ole Scalaa:
class Pos(val x: Double, val y: Double):
// ...
def xDiff(another: Pos) = palauta luku, joka on parametriksi annetun sijaintiolion
x-koordinaatin ja oman x-koordinaattisi erotus
def yDiff(another: Pos) = (sama mutta y-koordinaatille)
end Pos
Tuo hahmotelma on eräänlaista pseudokoodia ("valekoodia"; pseudocode) eli ohjelmakoodia muistuttavaa mutta vain ihmislukijalle tarkoitettua tekstiä. Tässä pseudokoodissamme osa ilmaisuista on jo valmista Scalaa, mutta eräitä keskeisiä kohtia on vasta ideoitu suomeksi.
Pseudokoodi Scalaksi
Miten toteuttaisit äskeisen pseudokoodin Scalalla? Mieti ensin itse! Kirjoita tarvittava koodi vaikka paperille. Se ei ole pitkä.
Voit myös katsoa seuraavan animaation, joka voi auttaa ratkaisun löytämisessä. Valmis ohjelmakoodi löytyy aivan animaation lopusta. Juuri ennen paljastusta tulee varoitus, jottet näytä sitä itsellesi vahingossa etukäteen.
Huomasithan, miten metodin koodissa voi viitata sekä metodia suorittavan olion omiin
ominaisuuksiin (esim. this.x) että toisen olion ominaisuuksiin (tässä muuttujan
another kautta: another.x)?
Huomaa vielä: another on tässä ihan tavallinen muuttujan nimi, ei mikään
ohjelmointikielen avainsana kuten this. Tuon sanan voisi korvata toisellakin
vaikuttamatta ohjelman toimintaan.
Vielä yksi etäisyysmetodi
Luonnostellaan metodi distance, joka laskee sijaintien etäisyyden suoraa viivaa pitkin:
val eka = Pos(50, 12.5)eka: Pos = Pos@3245f574 val toka = Pos(-30, 100)toka: Pos = Pos@2fcad1a3 toka.distance(eka)res14: Double = 118.55905701379376 eka.distance(toka)res15: Double = 118.55905701379376
Seuraava pseudokoodi hyödyntää suorakulmaisen kolmion
lisäksi ajatusta sitä, että olio voi kutsua omaa metodiaan eli "kysyä itseltään asioita"
(vrt. Henkilo-luokka edellisen luvun lopussa).
class Pos(val x: Double, val y: Double):
// ...
def xDiff(another: Pos) = another.x - this.x
def yDiff(another: Pos) = another.y - this.y
def distance(somePos: Pos) = Kysy itseltäsi, mitkä ovat oma xDiffisi ja yDiffisi
parametrina annettuun sijaintiolioon verrattuna. Laske
etäisyys sellaisesta suorakulmaisesta kolmiosta, jossa nuo
kaksi ovat kateettien mitat.
end Pos
Oman metodin kutsuminen sujuu yksinkertaisesti muodossa this.metodi(parametrit):
import scala.math.hypot
class Pos(val x: Double, val y: Double):
// ...
def xDiff(another: Pos) = another.x - this.x
def yDiff(another: Pos) = another.y - this.y
def distance(somePos: Pos) = hypot(this.xDiff(somePos), this.yDiff(somePos))
end Pos
Olio, joka vastaanottaa distance-metodikutsun, kutsuu omia
xDiff- ja yDiff-metodeitaan.
Matematiikkapakkauksen hypot-funktio (luku 1.6) hoitaa loput.
Tässä parametrimuuttuja on tarkoituksella nimetty eri tavoin.
Kyllä another tms. kävisi myös.
Pseudokoodista
Ohjelmoijat käyttävät pseudokoodia muun muassa algoritmien hahmottelemiseen sekä ratkaisujen kuvailemiseen enemmän tai vähemmän ohjelmointikieliriippumattomasti.
On paljon erilaisia tapoja kirjoittaa pseudokoodia. Äskeisen kaltaista pseudokoodia, joka sekoittaa puhdasta Scalaa ja varsin vapaamuotoista suomea, käytetään jatkossa taajasti tässä kurssimateriaalissa. Monesti teemme niin, että ensin laaditaan suurpiirteinen pseudokoodikuvaus ratkaisusta, sitten yksityiskohtaisempi pseudokoodi ja lopulta pseudokoodin kuvaama ajatus kirjoitetaan Scalaksi.
Voit — ja kannattaa! — itsekin luonnostella kurssin ohjelmointitehtävien ratkaisuja pseudokoodina joko paperilla tai editorissa.
Olioiden tekstikuvauksista
Tässä välissä käytämme hetken näppäröittääksemme Pos- ja Odds-luokkien käyttöä.
Ikävää mössöä
Aiemmassa REPL-esimerkissä luki näin:
val eka = Pos(50, 12.5)eka: Pos = Pos@3245f574
Vastaavaa merkkipuuroa saa näkyviin näinkin:
println(eka)Pos@3245f574 "Sijainti on: " + ekares16: String = Sijainti on: Pos@3245f574
Nuo Pos@3245f574-merkinnät eivät ole kovin kauniita tai hyödyllisiä. description-metodin palauttama kuvaus kertoo paljon enemmän luodusta Pos-oliosta. Vastaavasti
Odds-olioiden kanssa jouduimme kutsumaan fractional-metodia aina uudestaan.
On käytännöllistä pystyä muodostamaan oliosta merkkijonomuotoinen kuvaus. Sellaisista on usein apua luokkia koekäyttäessä ja testatessa (esim. REPLissä) sekä monissa virheenetsintätilanteissa.
Koska tarve on yleinen, olisi kiva, jos kuvauksien käsittely olisi mahdollisimman
kätevää. Esimerkiksi Pos-luokka voisikin toimia REPLissä seuraavasti.
val eka = Pos(50, 12.5)eka: Pos = (50.0,12.5) println(eka)(50.0,12.5) "Sijainti on: " + ekares17: String = Sijainti on: (50.0,12.5)
Toive: kun REPLiin kirjoittaa Pos-tyyppisen lausekkeen,
tulostuu sijainnin kuvaus eikä epäselvä merkintä kuten
Pos@3245f574.
Toive: viittauksen olioon voi antaa println-käskylle
parametriksi, ja tällöin tulostuu olion merkkijonokuvaus. Ei
tarvitse erikseen sanoa println(eka.description) tai vastaavaa.
Toive: myös silloin, kun plus-operaattori yhdistää merkkijonon
ja viittauksen Pos-olioon, saadaan merkkijono, jonka osana on
olion merkkijonokuvaus.
Kaikki toiveemme toteutuvat.
Eroon mössöstä toString-metodilla
Kaikille Scala-olioille on aina automaattisesti määritelty parametriton metodi nimeltä
toString, joka tuottaa merkkijonokuvauksen oliosta. Sitä voi kutsua Pos-olioillekin,
mutta ilman lisämäärittelyjä se tuottaa vain tutunnäköisen epähavainnollisen merkkijonon:
eka.toStringres18: String = Pos@3245f574
Kuitenkin voimme määritellä, että tietyntyyppisille oliolle kuvaus muodostetaan tietyllä
luokkakohtaisella tavalla. Toisin sanoen: korvataan epähavainnollinen oletusversio
toString-metodista sellaisella, joka sopii tiettyyn luokkaan. Kun tämä on tehty, tulee
korvaava toString-toteutus kutsutuksi tietyissä yhteyksissä automaattisesti, ilman
että kutsumista tarvitsee erikseen koodiin kirjoittaa. Esimerkiksi REPL kutsuu aina
olion toString-metodia, kun sen tulee näyttää olioarvoisen lausekkeen arvo. Samoin
println-funktio osaa kutsua sille annetun olion toString-metodia määrittääkseen,
mitkä merkit pitäisi tulostaa.
Alla on hieman muokattu versio Pos-luokasta. Kun luokka on määritelty näin, niin se
toimii REPLissä juuri niin kuin yllä toivottiin.
class Pos(val x: Double, val y: Double):
override def toString = "(" + this.x + "," + this.y + ")"
// ...
end Pos
description-metodin nimeksi on vaihdettu toString.
Määrittelyn alkuun on lisätty override-sana merkiksi siitä,
että korvataan olioiden oletusarvoinen toString-toteutus.
Tässä käytettiin samaa sanaa override kuin edellisen luvun lopun Teräsmies-esimerkissä,
ja kyse on tosiaan samasta asiasta: aiemmassa esimerkissä korvasimme henkilöluokallemme
yleisesti määritellyn metodin tietyssä henkilöoliossa, ja nyt korvasimme kaikille
Scala-olioille yleisesti määritellyn metodin kaikissa tietyn luokan olioissa.
Odds-tehtävä (osa 3/9)
Kehitä Odds-luokkaan toString-metodi:
toStringin tulee palauttaa täsmälleen samanlainen merkkijono kuin minkäfractional-metodikin palauttaa.Älä kuitenkaan poista
fractional-metodia. Voit sen sijaan toteuttaatoString-metodin niin, että kutsut siitäfractionalia.
Kokeile ratkaisusi toimivuutta REPLissä. Kun luot Odds-olion, näkyykö o1.Odds@a5e42e-tyyppisen rimpsun sijaan selkeämpi tuloste?
Kun metodisi toimii, tämän pitäisi tulostaa yksinkertaisesti 1/1000000:
println(Odds(1, 1000000))
Kokeile myös seuraavaa.
val six = Odds(5, 1)
println("The odds are: " + six)
println("The reverse odds are: " + six.not)
Tuossa yhdistetään merkkijonoihin viittauksia Odds-olioihin. Käytännössä siis rivit
kutsuvat toString-metodia, yhdistävät sen paluuarvon toiseen merkkijonoon ja
välittävät yhdistelmämerkkijonon println-käskylle.
A+ esittää tässä kohdassa tehtävän palautuslomakkeen.
Pikkutehtävä: rekursio ja toString-metodi
Odds-tehtävä (osa 4/9)
Myös tässä tehtävässä laadittavien metodien testaaminen on kätevämpää nyt, kun toString
on kunnossa.
Pohjustus
Tarkastellaan taas kuutosen heittämistä nopalla (5/1) ja klaavan heittämistä kolikolla
(1/1).
Todennäköisyys sille, että noppaa ja kolikkoa kerran heittämällä saadaan sekä kuutonen
että klaava voidaan kuvata Odds-oliona 11/1. Yleisemmin: jos alkuperäiset
todennäköisyydet ovat a1/a2 ja b1/b2,
niin todennäköisyys molempien toteutumiselle saadaan laskemalla
(a1⋅b1 + a1⋅b2 + a2⋅b1) ∕ (a2⋅b2).
Esimerkkitapauksessamme alkuperäiset luvut ovat 5/1 ja 1/1, joten saadaan (5⋅1 + 5⋅1 + 1⋅1) ∕ (1⋅1)
eli 11/1.
Todennäköisyys sille, että saadaan joko kuutonen tai klaava tai molemmat, voidaan
kuvata Odds-oliona 5/7. Vastaava kaava on
(a1⋅b1) ∕ (a1⋅b2 + a2⋅b1 + a2⋅b2).
Esimerkkitapauksessamme siis 5/1 ja 1/1 tuottavat tuloksen (5⋅1) ∕ (5⋅1 + 1⋅1 + 1⋅1) eli 5/7.
Tehtävänanto
Kirjoita Odds-luokkaan kaksi vaikutuksetonta metodia, joilla voidaan määrittää
todennäköisyydet sille, että kumpikin kahdesta tapahtumasta (both) tai ainakin
toinen (either) toteutuu. Metodien tulee toimia tähän tapaan:
val six = Odds(5, 1)six: Odds = 5/1 val tails = Odds(1, 1)tails: Odds = 1/1 val sixAndTails = six.both(tails)sixAndTails: Odds = 11/1 six.either(tails)res19: Odds = 5/7
both- ja either-metodit eivät palauta merkkijonoja
(String)! Ne palauttavat viittauksia uusiin Odds-luokan
ilmentymiin.
Ohjeita ja vinkkejä
Kiinnitä huomiota metodien paluuarvojen tyyppeihin. Metodit palauttavat viittauksia
Odds-olioihin, eivät esimerkiksi merkkijonoja.Tarvittava matematiikka on annettu yllä. Ratkaisussasi sinun täytyy vain
kirjoittaa nuo annetut kaavat Scalaksi
luoda uusi
Odds-olio, johon laskutulokset on tallennettu, ja palauttaa viittaus siihen.
Metodeissa on paljon samaa kuin edeltä tutuissa toisissa metodeissa:
On otettava parametrina toinen olio, jota käytetään tuloksen muodostamisessa. (Vrt.
Pos-luokanxDiffjayDiff.)On muodostettava tulos
Odds-luokan muuttujien arvoista. (Vrt.not-metodi; nyt on vain pidemmät kaavat.)On palautettava tuloksena uusi samantyyppinen olio. (Vrt.
Pos-luokanadd-metodit, jotka luovat uusiaPos-olioita.)
Pyydä lisävinkkiä henkilökunnalta, jos jäät jumiin!
A+ esittää tässä kohdassa tehtävän palautuslomakkeen.
Tarkoitushan oli hyödyntää sijaintiluokkaa kuvien käsittelyssä
Pos-luokka on tarjolla kurssipakkauksessa o1. Tulemme käyttämään sitä paljon.
val vasenYlakulma = Pos(0, 0)vasenYlakulma: Pos = (0.0,0.0)
Luokasta löytyvät tässä luvussa esitellyt metodit ja aika monta muutakin.
Lisäksi tutulla Pic-luokalla on monia toistaiseksi epätuttuja metodeita, joita
kutsuessa voimme kohdentaa kuvankäsittelytoimintoja Pos-tyyppisillä parametreilla.
Kuvien asemointi kuvaan
val taivas = rectangle(1000, 400, LightBlue)taivas: Pic = rectangle-shape
val otokka = Pic("ladybug.png")otokka: Pic = ladybug.png
val yhdistelma = taivas.place(otokka, Pos(100, 300))yhdistelma: Pic = combined pic
show(yhdistelma)
place-metodille kerrotaan mihin kohtaan alempaa kuvaa päälle
asemoitavan kuvan keskipiste halutaan.
Metodi palauttaa viittauksen kuvien yhdistelmää vastaavaan olioon
samaan tapaan kuin aiemmin kohdatut above, leftOf jne.
Voit kokeilla itse myös muilla lukuarvoilla ja kuvilla. Kokeile myös lisätä useita kuvia eri paikkoihin samaa taustaa vasten. Vaikka näin:
val taivas = rectangle(1000, 400, LightBlue)taivas: Pic = rectangle-shape
val otokka = Pic("ladybug.png")otokka: Pic = ladybug.png
val monoliitti = rectangle(100, 300, Black)monoliitti: Pic = rectangle-shape
val otokanSijainti = Pos(400, 200)otokanSijainti: Pos = (500,200)
val kuva = taivas.place(otokka, otokanSijainti).place(monoliitti, otokanSijainti.addX(150))kuva: Pic = combined pic
show(kuva)
Tämä on lisäesimerkki siitä, että metodikutsuja voi panna...
... paitsi sisäkkäin...
... myös ketjuun. Tässä ensimmäisen lisäyksen tuottamaan kuvaan asemoidaan myös toinen kuva.
Usein kysyttyä: Miksi y-koordinaatit kasvavat alaspäin?
Tässä luvussa, kuten kaksiulotteisessa tietokonegrafiikassa usein muutenkin, käytetään koordinaatistoa, jossa y-koordinaatti kasvaa alaspäin toisin kuin matematiikassa yleensä. Pääsyyt tälle ehkä yllättävälle koordinaatistolle ovat historialliset ja liittyvät monitoritekniikkaan.
Asemointitehtäviä
Ota esille Aliohjelmia-moduuli ja sen kierros2.scala. Vaikkei nyt ihan nenäpäivä olisikaan, niin ole hengessä
mukana ja kirjoita sinne funktio nenita, jota voi käyttää näin:
val alkuperainen = Pic("defense.png")alkuperainen: Pic = defense.png
val uusittu = nenita(alkuperainen, Pos(240, 245))uusittu: Pic = combined pic
show(uusittu)
nenita-funktio palauttaa uuden kuvan, jossa ensimmäisen
parametrin osoittaman taideteoksen päälle on piiretty punainen
ympyrä, jonka halkaisija on viisitoista pikseliä.
Toinen parametri kertoo kohdan, johon tuo punainen "nenä" piirretään.
nenita-funktio ei laita muodostamaansa kuvaa näkyviin, vaan
palauttaa sen. Tuon kuvan voi kyllä tuoda näkyviin antamalla
sen parametriksi show’lle.
Huomaa testatessasi avata REPLiin juuri Aliohjelmia-moduuli.
A+ esittää tässä kohdassa tehtävän palautuslomakkeen.
Jälleen kerran: jokaisen metodin yksityiskohtia ei tarvitse opetella heti muistamaan
ulkoa. Palaa tähän lukuun tai Pic-luokan dokumentaatioon kertaamaan
tarpeen mukaan.
Luvun lopussa on esitelty vielä eräitä muita kuvien toimintoja. Niiden tunteminen ei ole jatkon kannalta välttämätöntä, mutta niistä voi olla muuten iloa ja näiden lisätehtävien tekeminen voi parantaa ohjelmointirutiiniasi.
Kuvan rajaaminen
crop-metodi
Rajausmetodia crop voi käyttää esimerkiksi näin:
val kuva = Pic("valkoparta.png")kuva: Pic = valkoparta.png
show(kuva)show(kuva.crop(Pos(40, 160), 125, 200))
Ensimmäinen parametri on kuvasta valitun rajauksen vasen yläkulma.
Toinen ja kolmas parametri kertovat rajauksen leveyden ja korkeuden pikseleinä.
Tehtävä: cropataan vasemmalta ja oikealta
Laadi vaikutuksettomat funktiot vasemmalta ja oikealta, joilla
voi poimia kuvasta vasemman tai oikean laidan. Ensimmäiseksi
parametriksi annetaan alkuperäinen kuva. Toiseksi parametriksi
annetaan Double, joka kertoo rajauksen koon suhteessa alkuperäisen
kuvan leveyteen. Esimerkiksi vasemmalta(puu, 33.3) palauttaa kuvan,
jossa on 33,3 % puun vasemmasta reunasta lukien, ja oikealta(puu, 50)
palauttaa puun kuvan oikean puoliskon.
Voit olettaa, että annettu luku on välillä 0–100. Muista, että
kuvilla on ominaisuudet width ja height ja että koordinaatit
alkavat nollasta. Viidenkymmenen pikselin levyisen kuvan
x-koordinaatit ovat siis välillä 0–49.
Kirjoita kierros2.scalaan samannimisessä moduulissa.
A+ esittää tässä kohdassa tehtävän palautuslomakkeen.
Ratkaise kuva-arvoitus
MAD-lehdessä julkaistiin vuoteen 2010 saakka kantaaottavia visuaalisia vitsejä, joiden jekku paljastui taittamalla aukeaman keskiosa piiloon vasemman ja oikean reunan alle.
Laadi vaikutukseton funktio, jolla voi virtuaalisesti taitella kuvan samaan tapaan. Funktion tulee ottaa parametreiksi kuva ja prosenttiosuus, joka jätetään näkyviin sekä vasemmalta että oikealta. Käyttöesimerkki:
val taittelematon = Pic("https://i.imgur.com/Rj6fcr6.png")taittelematon: Pic = https://i.imgur.com/Rj6fcr6.png
show(taittelematon)val taiteltu = taittele(taittelematon, 26.2)taiteltu: Pic = combined pic
show(taiteltu)
Käytä edellisen tehtävän vasemmalta- ja oikealta-funktioita.
Asemoi palat vierekkäin luvun 2.3 konstein.
A+ esittää tässä kohdassa tehtävän palautuslomakkeen.
Kätevämpää kuvien asemointia
Kuvien ankkurit
Palataan leppäkerttuesimerkkiin:
val taivas = rectangle(1000, 400, LightBlue)taivas: Pic = rectangle-shape
val otokka = Pic("ladybug.png")otokka: Pic = ladybug.png
val yhdistelma = taivas.place(otokka, Pos(100, 300))yhdistelma: Pic = combined pic
Näin syntyvässä yhdistelmässä koordinaatteihin (100,300) tulee asemoiduksi nimenomaan ötökkäkuvan keskikohta. Jos olisimme käyttäneet koordinaatteja (0,0), taustan vasempaan yläkulmaan tulisi näkyviin ötökän oikea alaneljännes. (Kokeile!) Voit ajatella, että ötökän keskellä on nasta, josta ötökkä kiinnitetään. Tosin kutsumme tuota kiinnityskohtaa nastan sijaan ankkuriksi:
otokka.anchorres20: Anchor = Center
Kaikilla Pic-olioilla on kiinnityskohta,
minkä voi todeta anchor-muuttujan arvon
katsomalla.
Ellei toisin määritellä, ankkuri on kuvan
äärikoordinaattien puolivälistä löytyvä
keskikohta, joka on tässä kuvailtu sanalla
Center.
Ankkureita varten on o1-pakkauksessa oma
tietotyyppinsä Anchor.
Varsin moneen tarkoitukseen sopii hyvin ankkuroida kuva keskeltä. Silti vaihtoehdoillekin on usein käyttöä, ja niitä kyllä löytyy. Tutkitaan:
show(taivas.place(otokka, Center, Pos(0, 0)))
Keskimmäinen parametri on tyyppiä Anchor
ja kertoo, että juuri ötökän keskikohta
tulee sijoittaa kohtaan (0,0). Huomaa, että
kyseessä ei ole merkkijono eikä tämä arvo
siis ole lainausmerkeissä.
Tuo käsky siis vielä toimi ihan tutusti ja ankkuroi kuvan keskikohdastaan, mutta samalla se paljasti, että voimme vaihtaa kiinnityskohtaa. Kokeile näitä:
show(taivas.place(otokka, TopLeft, Pos(0, 0)))show(taivas.place(otokka, CenterLeft, Pos(0, 0)))
Entä miksei seuraava place-käsky "tee mitään"?
show(taivas.place(otokka, TopRight, Pos(0, 0)))
Ankkuriparametreiksi sopivat TopLeft, TopCenter, TopRight, CenterLeft,
Center, CenterRight, BottomLeft, BottomCenter ja BottomRight.
Ankkuri vasten ankkuria
Edellä käytimme absoluuttisia koordinaatteja kuten (0,0) kirjataksemme mihin kohtaan taustakuvaa ylemmän kuvan ankkuri kiinnitetään. Samaan tapaan alla on käytetty sijaintia (100,225).
val runko = rectangle(30, 250, SaddleBrown)
val lehvisto = circle(200, ForestGreen)
val puu = runko.onto(lehvisto, Pos(100, 225))
Nuo luvut eivät toimi sattumalta. Ne on pitänyt laskea sillä perusteella, että:
100 on puolivälissä lehvistöä.
225 on 125 pistettä (eli puolet rungon mitasta) alempana kuin lehvistön puoliväli.
Erikseen ohjelman ulkopuolella laskeskelemalla on näin saatu aikaan, että rungon yläreunan keskusta on juuri lehvistön keskipisteen kohdalla. Hieman vaivalloista, ja mikä tärkeämpää, jos muutamme lehvistön tai rungon kokoa, meidän pitää muistaa ja viitsiä laskea myös nuo luvut uudestaan. Ikävää on sekin, että koodin lukija joutuu miettimään, mistä nuo luvut nyt tulivatkaan.
Kätevämpi ja kauniimpi koodi:
val runko = rectangle(30, 250, SaddleBrown)
val lehvisto = circle(200, ForestGreen)
val puu = runko.onto(lehvisto, TopCenter, Center)
Pic-luokan metodit sallivat meidän määritellä
ankkurilla paitsi päälle kiinnitettävän kuvan
kohdan (rungon yläreunan keskikohta) myös taemman
kuvan kohdan, johon se kiinnitetään (lehvistön
keskipiste).
Tässä vielä koottu esimerkki, jossa muodostetaan opittuja käskyjä käyttäen maisema, jossa on taivas, maa, puu ja ötökkä. Voit tutustua esimerkin koodiin, ennustaa millainen kuvasta tulee ja katsoa ennustitko oikein.
val taivas = rectangle(1000, 400, LightBlue)
val maa = rectangle(1000, 50, SandyBrown)
val otokka = Pic("ladybug.png")
val runko = rectangle(30, 250, SaddleBrown)
val lehvisto = circle(200, ForestGreen)
val puu = runko.onto(lehvisto, TopCenter, Center)
val maaJaPuu = puu.onto(maa, BottomCenter, Pos(500, 30))
val maisema = taivas.place(maaJaPuu, BottomLeft, BottomLeft).place(otokka, Pos(100, 300))
Ankkurointitehtävä

Laadi vaikutukseton funktio tsekinLippu, joka
ottaa ainoaksi parametrikseen lipun leveyden
Doublena, japalauttaa tuonlevyisen kuvan Tšekin lipusta, jonka
korkeus on kaksi kolmasosaa leveydestä
vasemmassa laidassa on tasakylkinen kolmio, jonka kärki ylettää lipun keskipisteeseen
värit ovat
MidnightBlue,WhitejaCrimson.
Tasakylkisen kolmion saa käskyllä triangle(leveys, korkeus, väri).
Näin luodun kolmion kyljet ovat sivuilla ja kanta alhaalla.
Tehtävän voi periaatteessa ratkaista ilmankin, mutta se on hyvä tilaisuus harjoitella ankkurien käyttöä. Harjoittele ankkurien käyttöä.
Keksitkö useita tapoja asemoida kolmion?
Kirjoita tämäkin funktio Aliohjelmia-moduuliin, kierros2.scalaan.
A+ esittää tässä kohdassa tehtävän palautuslomakkeen.
Yhteenvetoa
Määrittelemällä luokkaan metodeita voimme luoda säännöstön, joka säätelee, miten tietynlaisia arvoja — tuon luokan ilmentymiä — voi yhdistellä ja miten tällöin syntyy uusia ilmentymiä.
Esimerkkejä tällaisesta kurssillamme ovat luokat
Pos,OddsjaPic.Vertaa: matemaattinen säännöstö, joka määrää, miten lukuja eri operaatioin yhdistelemällä syntyy uusia lukuja.
Ohjelmoija voi käyttää pseudokoodia eli ohjelmakoodia muistuttavaa tekstiä työvälineenä esimerkiksi ratkaisuja hahmotellessaan.
Scala-luokkaan voi laatia
toString-nimisen metodin, joka palauttaa kuvauksen oliosta. Tämä voi kätevöittää muun muassa kyseisentyyppisten olioiden testausta.Pakkauksen
o1tarjoamaPos-luokka kuvaa koordinaattipareja. YhdessäPic-luokan kanssa käytettynä se mahdollistaa monia kuvankäsittelytoimintoja.Lukuun liittyviä termejä sanastosivulla: luokka, ilmentymä, viittaus; pseudokoodi;
toString, korvata; ankkuri.
Palaute
Huomaathan, että tämä on henkilökohtainen osio! Vaikka olisit tehnyt lukuun liittyvät tehtävät parin kanssa, täytä palautelomake itse.
Tekijät
Tämän oppimateriaalin kehitystyössä on käytetty apuna tuhansilta opiskelijoilta kerättyä palautetta. Kiitos!
Materiaalin luvut tehtävineen ja viikkokoosteineen on laatinut Juha Sorva.
Liitesivut (sanasto, Scala-kooste, usein kysytyt kysymykset jne.) on kirjoittanut Juha Sorva sikäli kuin sivulla ei ole toisin mainittu.
Tehtävien automaattisen arvioinnin ovat toteuttaneet: (aakkosjärjestyksessä) Riku Autio, Nikolas Drosdek, Kaisa Ek, Joonatan Honkamaa, Antti Immonen, Jaakko Kantojärvi, Niklas Kröger, Kalle Laitinen, Teemu Lehtinen, Mikael Lenander, Ilona Ma, Jaakko Nakaza, Strasdosky Otewa, Timi Seppälä, Teemu Sirkiä, Anna Valldeoriola Cardó ja Aleksi Vartiainen.
Lukujen alkuja koristavat kuvat ja muut vastaavat kuvituskuvat on piirtänyt Christina Lassheikki.
Yksityiskohtaiset animaatiot Scala-ohjelmien suorituksen vaiheista suunnittelivat Juha Sorva ja Teemu Sirkiä. Teemu Sirkiä ja Riku Autio toteuttivat ne apunaan Teemun aiemmin rakentamat työkalut Jsvee ja Kelmu.
Muut diagrammit ja materiaaliin upotetut vuorovaikutteiset esitykset laati Juha Sorva.
O1Library-ohjelmakirjaston ovat kehittäneet Aleksi Lukkarinen ja Juha Sorva. Useat sen keskeisistä osista tukeutuvat Aleksin SMCL-kirjastoon.
Tapa, jolla käytämme O1Libraryn työkaluja (kuten Pic) yksinkertaiseen graafiseen
ohjelmointiin, on saanut vaikutteita tekijöiden Flatt, Felleisen, Findler ja Krishnamurthi
oppikirjasta How to Design Programs sekä Stephen Blochin oppikirjasta Picturing Programs.
Oppimisalusta A+ luotiin alun perin Aallon LeTech-tutkimusryhmässä pitkälti opiskelijavoimin. Nykyään tätä avoimen lähdekoodin projektia kehittää Tietotekniikan laitoksen opetusteknologiatiimi ja tarjoaa palveluna laitoksen IT-tuki. Pääkehittäjänä on nyt Markku Riekkinen, jonka lisäksi A+:aa ovat kehittäneet kymmenet Aallon opiskelijat ja muut.
A+ Courses -lisäosa, joka tukee A+:aa ja O1-kurssia IntelliJ-ohjelmointiympäristössä, on toinen avoin projekti. Sen suunnitteluun ja toteutukseen on osallistunut useita opiskelijoita yhteistyössä O1-kurssin opettajien kanssa.
Kurssin tämänhetkinen henkilökunta löytyy luvusta 1.1.
Lisäkiitokset tähän lukuun
MAD-lehden taittokuvavitsit loi edesmennyt Al Jaffee.
Nenittämämme maalauksen maalasi Akseli Gallén-Kallela.
Luodaan uusi
Pos-olio kuvaamaan alkuperäisen suhteen määriteltyä koordinaattiparia.