Luet oppimateriaalin englanninkielistä versiota. Mainitsit kuitenkin taustakyselyssä osaavasi suomea. Siksi suosittelemme, että käytät suomenkielistä versiota, joka on testatumpi ja hieman laajempi ja muutenkin mukava.
Suomenkielinen materiaali kyllä esittelee englanninkielisetkin termit.
Kieli vaihtuu A+:n sivujen yläreunan painikkeesta. Tai tästä: Vaihda suomeksi.
Chapter 2.5: Pictures and Positions
About This Page
Questions Answered: How about some more example classes? What more can I do with a picture object? How do I make it more convenient to test objects in the REPL?
Topics: Methods that create and return instances; methods that
receive references to objects. The special method toString.
Image manipulation: positioning, cropping, etc.
What Will I Do? Multiple programming assignments interwoven with the text.
Rough Estimate of Workload:? Two hours, perhaps. More if you go through the optional material at the end. There are barely any genuinely new concepts, but the programming assignments may challenge the novice programmer.
Points Available: A50.
Related Modules: Odds. We’ll re-revisit Subprograms, too.

Our Next Objective: Locations within Pictures
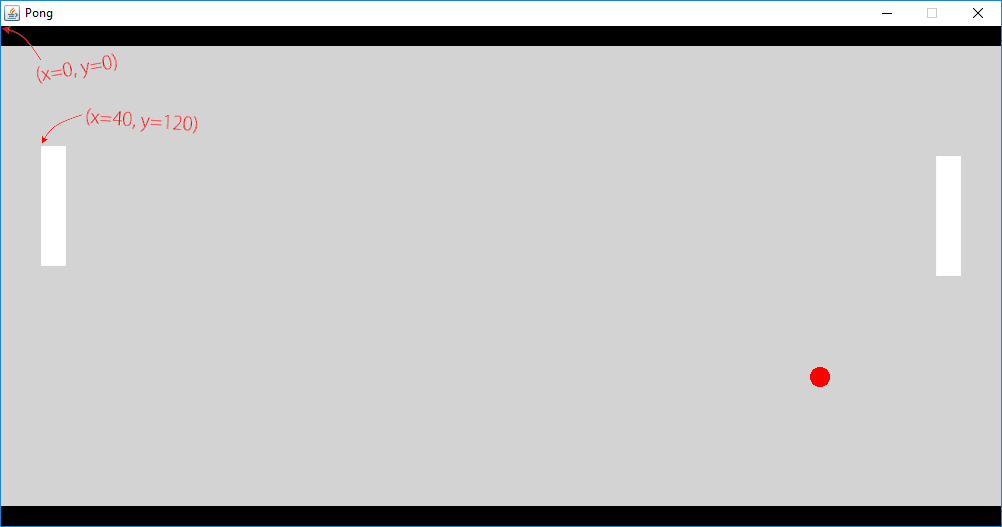
The top-left corner of a Pong paddle is located at (40,120), counting pixels from the top left. When programming graphics, it’s common to use coordinates that increase from left to right and from top to bottom.
Two-dimensional coordinates are a handy concept in many programs. You can use a pair of coordinates to represent the location of a character in a game, for example. Or, when working with images, you can use coordinates to pinpoint a specific pixel that you wish to target with an operation:
“Within this large image, select a square piece 400 pixels wide and high, so that its top-left corner is 150 pixels rightwards from the original’s left edge and 200 pixels down from the top edge.”
“Draw this small image on top of that larger one so that the small image’s center is exactly at (300,200) within the large image.”
“Draw a dot at the given coordinates (x,y), where x and y stand for the mouse cursor’s current position, counting from the top left.”
You’ll soon learn to issue Scala commands much like the ones expressed in English above.
Towards that end, we’ll first develop a class that represents pairs of coordinates. As
we do so, we’ll also apply what we learn to the Odds class from the previous chapter.
The class Pos(ition)
Let’s call our coordinate-pair class simply Pos. Perhaps it could work like this?
val first = Pos(50, 12.5)first: Pos = Pos@3245f574 val second = Pos(-30, 100)second: Pos = Pos@2fcad1a3 first.xres0: Double = 50.0 first.yres1: Double = 12.5 first.descriptionres2: String = (50.0,12.5) second.descriptionres3: String = (-30.0,100.0)
Using what we know, it’s easy to implement a class that works like that:
class Pos(val x: Double, val y: Double):
def description = "(" + this.x + "," + this.y + ")"
Of course, we could just forget about Pos and represent coordinates as two separate
Doubles. (Indeed, that’s what we did in Chapters 1.7 and 1.8 when we computed
distances between points.) But it’s advantageous to consider positions to be a data
type in their own right: a type that binds together a pair of numerical values (x and y)
and provides a selection of methods for manipulating such pairs. The advantages will
become increasingly clear as we go on.
If you want to try Pos in the REPL...
... just skip entering that class definition in the REPL.
A Pos class that corresponds to what’s presented in this
chapter is already predefined for you in the o1 package
and automatically available in the REPL. The existing class
has some additional functionality beyond the basic things
that were presented above.
Creating New Instances within a Method
Computing on Positions
It’s easy to conceive of operations that we can apply to a position to produce new positions. For instance, we might wish to compute a position that is located a given distance away from another position:
val topLeftCorner = Pos(40, 120)topLeftCorner: Pos = Pos@2c8d4d39 val aBitToTheRight = topLeftCorner.addX(30)aBitToTheRight: Pos = Pos@25b7325c
Notice: addX returned a reference to a new Pos object that represents a location
whose x coordinate is 30 units (such as pixels) greater than the position whose method
was called.
All the methods of a Pos are also available on the new position object, which the
variable aBitToTheRight now refers to:
aBitToTheRight.descriptionres4: String = (70.0,120.0) val moreToTheRight = aBitToTheRight.addX(70)moreToTheRight: Pos = Pos@2d9ff490 moreToTheRight.descriptionres5: String = (140.0,120.0)
Here’s an implementation for addX:
class Pos(val x: Double, val y: Double):
def description = "(" + this.x + "," + this.y + ")"
def addX(dx: Double) =
val relativePosition = Pos(this.x + dx, this.y)
relativePosition
end Pos
We compute the new position’s coordinates based on the
coordinates of the this object. The parameter variable dx
indicates the difference between the two positions. A simple sum
produces the new x coordinate; the new position has the same y as
the original.
We return a reference to the newly created object.
In the above version of the class, the local variable relativePosition was there merely
to emphasize the two-stage process: first, we create the object; then, we return a
reference that points to it. Here is short-and-sweet way to phrase the same:
class Pos(val x: Double, val y: Double):
def description = "(" + this.x + "," + this.y + ")"
def addX(dx: Double) = Pos(this.x + dx, this.y)
end Pos
When a method returns a reference, it’s up to the method’s caller to decide what to
do with that reference. In our earlier example, we happened to assign the reference
returned by addX to a variable (moreToTheRight), but we can just as well use the
method call as part of a larger expression. For example, we can form a chain of method
calls:
moreToTheRight.addX(100).descriptionres6: String = (240.0,120.0)
The Pos object’s addX method returns a reference to another
Pos. This calling code doesn’t store the reference in a
variable; it just immediately invokes description on the
returned object, producing a return value of type String.
We can of course define an addY method as an analogue of addX. The code below
additionally contains an add method that attends to both coordinates.
class Pos(val x: Double, val y: Double):
def description = "(" + this.x + "," + this.y + ")"
def addX(dx: Double) = Pos(this.x + dx, this.y)
def addY(dy: Double) = Pos(this.x, this.y + dy)
def add(dx: Double, dy: Double) = Pos(this.x + dx, this.y + dy)
end Pos
We now have a decent foundation for our Pos class. We’ll add more methods to it shortly.
On a more general level, we can say that we’ve defined not just a particular type of data
but a set of rules that govern how new instances get created as we compute with the type.
Assignment: Odds (Part 2 of 9)
Introduction
Let’s return for a bit to the Odds program that we initiated in Chapter 2.4.
Consider two events: say, rolling a six on a die (which has 5/1 odds of happening) and a coin toss coming up tails (1/1 odds).
val six = Odds(5, 1)six: Odds = o1.odds.Odds@60a6fd val tails = Odds(1, 1)tails: Odds = o1.odds.Odds@111a008
We can get the odds of not rolling a six by swapping the numbers: 1/5. A coin coming up heads has the same odds as it coming up tails, and indeed 1/1 is the same whichever way around.
More generally: if an object represents a1/a2 odds, the odds of the opposite event are a2/a1.
Task description
Add a not method to Odds. This effect-free method creates an object that
represents the odds of the opposite event. It should work like this:
val somethingOtherThanSix = six.notres7: Odds = o1.odds.Odds@56258cb3 somethingOtherThanSix.fractionalres8: String = 1/5 tails.not.fractionalres9: String = 1/1 Odds(10, 19).not.fractionalres10: String = 19/10
Instructions and hints
The method must create a new
Oddsinstance and return a reference to that object. It mustn’t return just a string or a number.You need to write very little code.
A+ presents the exercise submission form here.
Parameters That Refer to Instances
Pseudocode for determining distances
Turning again to class Pos, let’s add two methods called xDiff and yDiff, which
compute the distance between two positions along a single coordinate axis.
val first = Pos(50, 12.5)first: Pos = Pos@3245f574 val second = Pos(-30, 100)second: Pos = Pos@2fcad1a3 val differenceBetweenXCoordinates = second.xDiff(first)differenceBetweenXCoordinates: Double = 80.0 second.yDiff(first)res11: Double = -87.5 first.yDiff(second)res12: Double = 87.5 first.xDiff(Pos(60, 20))res13: Double = 10.0
Here’s a first sketch of the method implementations. This isn’t quite Scala yet:
class Pos(val x: Double, val y: Double):
// ...
def xDiff(another: Pos) = return a number that is the difference between the given
object’s x coordinate and your own x coordinate
def yDiff(another: Pos) = (the same but for the objects’ y coordinates)
end Pos
The sketch is written in pseudocode (pseudokoodi): text that resembles program code but is meant only for a human reader. In the pseudocode that we’ve used here, some parts are actual Scala but some key parts have been only outlined in English.
From pseudocode to Scala
How would you implement the above pseudocode in Scala? Stop and think. Write the required code on a piece of paper, for instance. It’s not long.
The following animation may help you answer the question. The full program code will appear at the very end of the animation. You’ll be warned before that happens, so don’t worry about spoilers.
Notice how you can refer to both the attributes of the object running the method (e.g.,
this.x) and the attributes of another object (here using a variable named another:
another.x)?
Also note: another is just a regular variable name, not a programming-language keyword
like this. We could replace the word “another” with something else without affecting
the program’s behavior.
One more distance method
The method distance should compute the distance between two positions along a straight
line:
val first = Pos(50, 12.5)first: Pos = Pos@3245f574 val second = Pos(-30, 100)second: Pos = Pos@2fcad1a3 second.distance(first)res14: Double = 118.55905701379376 first.distance(second)res15: Double = 118.55905701379376
The algorithm described in the following pseudocode uses a right triangle. Moreover, it makes use of the idea that an object can call its own method to “ask itself stuff”.
class Pos(val x: Double, val y: Double):
// ...
def xDiff(another: Pos) = another.x - this.x
def yDiff(another: Pos) = another.y - this.y
def distance(somePos: Pos) = Ask yourself: what are your own xDiff and yDiff relative to the
other position provided as a parameter? Compute the two-dimensional
distance from a right triangle that has those two values as legs.
end Pos
To make an object call its own method, we simply write this.methodName(parameters).
(This is similar to how a Person commanded itself at the end of the previous chapter.)
import scala.math.hypot
class Pos(val x: Double, val y: Double):
// ...
def xDiff(another: Pos) = another.x - this.x
def yDiff(another: Pos) = another.y - this.y
def distance(somePos: Pos) = hypot(this.xDiff(somePos), this.yDiff(somePos))
end Pos
The object whose distance method has been called calls its own
xDiff and yDiff methods.
The function hypot from Scala’s math package (Chapter 1.6)
takes care of the rest.
Just to illustrate, we’ve deliberately used a different name
for the parameter variable here. We could have also called it
another, or something else.
On Pseudocode
Programmers use pseudocode for several purposes, primarily to sketch out solutions or to describe algorithms in a more or less programming-language-independent form.
There are many different ways to write pseudocode. In O1, we’ll continue to use the sort of pseudocode that we used above, combining actual Scala with informal natural language. We’ll often start solving a problem by drafting an overall solution in pseudocode, follow that with a more refined pseudocode, and finally express the solution in plain Scala.
You can — you should! — use pseudocode on your own, too, as you sketch out solutions to programming assignments. Use a piece of paper or an editor, as you prefer.
Describing Objects as Text
Let’s take a moment to make both Pos and Odds easier to experiment with.
Unpleasant porridge
Our earlier REPL example featured this bit:
val first = Pos(50, 12.5)first: Pos = Pos@3245f574
Other commands serve up a similar porridge of characters:
println(first)Pos@3245f574 "The location is: " + firstres16: String = The location is: Pos@3245f574
The text Pos@3245f574 is neither pretty nor useful to us. To see a more descriptive
string representation of the Pos object we created, we have to call the object’s
description method. Similarly, when working with Odds objects, we’ve had to call
methods such as fractional to view any actual information about the object.
It’s useful to be able to form string representations of objects. For one thing, such descriptions are convenient when testing a class (in the REPL, for example) or when searching for errors in one’s program.
Since the need is common, it should be easy to form and view descriptions. For
example, wouldn’t it be nice if we could use Pos in the REPL like this?
val first = Pos(50, 12.5)first: Pos = (50.0,12.5) println(first)(50.0,12.5) "The location is: " + firstres17: String = The location is: (50.0,12.5)
We wish: when we enter an expression of type Pos in the REPL,
we get a proper description of the Pos object rather than
Pos@3245f574.
We wish: we may pass a reference to an object as a parameter to
println in order to print out a meaningful description. We
don’t have to make a separate method call to produce that text,
as in println(first.description).
We wish: if we use the plus operator to combine a string with an object, we get a string that contains the object’s textual description.
All our wishes are about to be fulfilled.
No more porridge: toString
Scala automatically furnishes every single object with a parameterless method named
toString, which returns a string describing the object. This method is available on
Pos objects, too, but unless we specify otherwise, it produces only the familiar,
unhelpful text:
first.toStringres18: String = Pos@3245f574
However, we can define a class-specific way of describing objects. In other words: we can
override the uninformative default toString with another implementation that works
well for a specific class. Once we do that, our overriding toString implementation
will be automatically called in certain circumstances. For example, the REPL always calls
an object’s toString method when it has evaluated an expression that refers to an object.
Similarly, if we pass an object reference to println, it invokes the object’s toString
method to determine which characters it should print out.
Below is a slightly modified version of class Pos. Defined like this, the class works
exactly as we wished earlier.
class Pos(val x: Double, val y: Double):
override def toString = "(" + this.x + "," + this.y + ")"
// ...
end Pos
We’ve changed the name of description to toString.
We use the override keyword to state that we’re redefining an
existing method and replace the default toString defined for all
objects with this Pos-specific implementation.
The word override already appeared in the Superman example at the end of the previous
chapter. In that earlier example, a method was generally defined for our Person
class, and we overrode it on an individual object; in the present example, a method has
been generally defined for all Scala objects, and we override it on all objects of type
Pos. In each of the two examples, the override keyword was both appropriate and
required.
Assignment: Odds (Part 3 of 9)
Develop a toString method in class Odds:
The method should return exactly the same string that
fractionalreturns.Don’t remove
fractional, however. What you can do instead is implementtoStringso that it callsfractional.
See if your solution works in the REPL. When you create an Odds object, do you get a
more informative printout rather than something like o1.odds.Odds@a5e42e?
When your method works, the following command should output simply 1/1000000:
println(Odds(1, 1000000))
Try this, too:
val six = Odds(5, 1)
println("The odds are: " + six)
println("The reverse odds are: " + six.not)
The above example concatenates strings with object references. In practice, this means
that these lines call toString on an object, combine the string returned by toString
with another string, and pass on the combination to println.
A+ presents the exercise submission form here.
Mini-Assignment: Recursion and toString
Assignment: Odds (Part 4 of 9)
You can immediately reap toString’s benefits as you test the additional methods that
you’re about to write.
Introduction
Consider, again, the events of rolling a six (5/1) and a coin coming up tails (1/1).
The odds of a single die roll and a single coin toss producing both a six and tails are 11/1. More generally: if the odds of two original events are a1/a2 and b1/b2, you can obtain the odds of both events occurring by computing (a1×b1 + a1×b2 + a2×b1) ∕ (a2×b2). In our example, the original odds were 5/1 and 1/1, from which we get (5×1 + 5×1 + 1×1) ∕ (1×1), which equals 11/1.
The odds for either rolling a six, or the coin coming up tails, or both happening, are 5/7. We can get those numbers from the formula (a1×b1) ∕ (a1×b2 + a2×b1 + a2×b2). In our example, the odds 5/1 and 1/1 combine to (5×1) ∕ (5×1 + 1×1 + 1×1), which equals 5/7.
Task description
In class Odds, add two effect-free methods that determine the odds that both of two
events occur (both), and the odds that at least one of two events occurs (either).
The methods should work as shown in the example below.
val six = Odds(5, 1)six: Odds = 5/1 val tails = Odds(1, 1)tails: Odds = 1/1 val sixAndTails = six.both(tails)sixAndTails: Odds = 11/1 six.either(tails)res19: Odds = 5/7
The both and either methods do not return Strings!
They return references to new instances of the Odds class.
Instructions and hints
Note the return values’ types. The methods return references to
Oddsobjects, not strings or numbers.All the necessary arithmetic has been provided for you above. To solve the assignment, all you need to do is this:
Write down the formulas in Scala.
Create a new
Oddsobject that stores the result and return a reference to that object.
These new methods are very similar to some other methods that you’ve already seen and written:
The new methods take in, as a parameter, another object that they use as they compute the result. This is similar to the
xDiffandyDiffmethods inPos.The new methods access the variables in
Oddsfor the values that the formula demands. This is similar to what you did when you wrotenot; it’s just that these new formulas are longer.The new methods need to create and return another object of the same type. This is similar to the
addmethods in classPos, which create newPosobjects.
Ask for help if you get stuck!
A+ presents the exercise submission form here.
Recall Our Plan: To Use Pos for Image Manipulation
The class Pos is available for you to use in package o1. We’ll be using it a lot.
val topLeftCorner = Pos(0, 0)topLeftCorner: Pos = (0.0,0.0)
The class has all the methods discussed in this chapter and quite a few others to boot.
Moreover, the Pic class, which you know, has a number of methods that you don’t yet
know and that use parameters of type Pos to target specific locations within images:
Positioning images onto an image
val sky = rectangle(1000, 400, LightBlue)sky: Pic = rectangle-shape
val bug = Pic("ladybug.png")bug: Pic = ladybug.png
val combination = sky.place(bug, Pos(100, 300))combination: Pic = combined pic
show(combination)
We specify the location within the background image where we wish the other image’s center to appear.
place returns a reference to a Pic object that represents
the combined image, much like above, leftOf, and other
familiar methods.
Experiment with place using other numbers and images. Try placing multiple images in
different places against the same background image. Like this, for instance:
val sky = rectangle(1000, 400, LightBlue)sky: Pic = rectangle-shape
val bug = Pic("ladybug.png")bug: Pic = ladybug.png
val monolith = rectangle(100, 300, Black)monolith: Pic = rectangle-shape
val bugLocation = Pos(400, 200)bugLocation: Pos = (400,200)
val myCreation = sky.place(bug, bugLocation).place(monolith, bugLocation.addX(150))myCreation: Pic = combined pic
show(myCreation)
This is another example of how we can not only...
... nest method calls one inside another, but also...
... chain them one after the other. In our example, we place another image (of a monolith) on top of the image we got when we placed another image (of a bug).
Frequently asked: Why does the y-axis “grow downwards”?
In this chapter, we’ve used a coordinate system where higher values
of y mean lower locations onscreen. This is perhaps surprising
and differs from what’s usual in mathematics; it is, however,
typical in two-dimensional computer graphics. The underlying
reasons are historical and have to do with monitor technology.
Practice positioning images
Open week2.scala in the Subprograms module. Even if it isn’t Red Nose Day today, celebrate it in spirit by writing
a clownify function that works as shown.
val originalArt = Pic("defense.png")originalArt: Pic = defense.png
val adaptation = clownify(originalArt, Pos(240, 245))adaptation: Pic = combined pic
show(adaptation)
clownify returns a new Pic where the artwork specified
by the first parameter has been augmented with a red circle
of fifteen pixels in diameter.
The second parameter indicates the position where the center of the red “nose” should appear.
clownify does not display the augmented picture, it merely
returns it. You can display the picture by passing it to show.
As you test your function, make sure your REPL is open in the Subprograms module.
A+ presents the exercise submission form here.
To reiterate: you don’t have to learn the details of each method by heart. Return to this
chapter or class Pic’s documentation for a recap as needed.
The rest of the chapter covers a few more operations on picture objects. Knowing these methods isn’t vital for success in O1, but you may find them fun to use. Working on the optional assignments below can also build up your fluency as a programmer.
Cropping an image
The crop method
The crop method selects a section of an image, discarding the rest:
val testPic = Pic("carton.png")testPic: Pic = carton.png
show(testPic)show(testPic.crop(Pos(20, 285), 190, 110))
The first parameter indicates the top-left corner of the rectangular cropping frame within the original.
The second and third parameter specify the cropping frame’s width and height.
Assignment: cropping left and right
Write two effect-free functions, leftSide and rightSide, that
select the left and right side of the original image, respectively.
Each receives a two parameters: the first is the original Pic,
and the second is a Double that specifies the size of the result
relative to the original’s width. For example, leftSide(tree, 33.3)
returns a picture that contains 33.3% of the original (the left
third), and rightSide(tree, 50) returns the right half.
You may assume that the given number is between 0 and 100. Remember
that Pics have width and height attributes and that the
coordinates run from zero upwards. (A picture 50 pixels wide spans
x coordinates from 0 to 49.)
Write your code in week2.scala in the Subprograms module.
A+ presents the exercise submission form here.
Solve an image puzzle
Until 2010, the back covers of MAD magazines featured topical visual jokes whose punchline was revealed by folding in the magazine so that the left- and right-hand sides of a picture covered the middle part.
Write an effect-free function that virtually folds in a picture. The function should take two parameters: the unfolded image and the percentage of the original image that will remain visible on both the left and the right.
Usage example:
val unfoldedPic = Pic("https://i.imgur.com/Rj6fcr6.png")unfoldedPic: Pic = https://i.imgur.com/Rj6fcr6.png
show(unfoldedPic)val foldedPic = foldIn(unfoldedPic, 26.2)foldedPic: Pic = combined pic
show(foldedPic)
Use leftSide and rightSide from the previous assignment. Use the tools from
Chapter 2.3 to place the pieces side by side.
A+ presents the exercise submission form here.
Positioning images with ease
Anchors in pictures
Here’s the ladybug example again:
val sky = rectangle(1000, 400, LightBlue)sky: Pic = rectangle-shape
val bug = Pic("ladybug.png")bug: Pic = ladybug.png
val combination = sky.place(bug, Pos(100, 300))combination: Pic = combined pic
In the combined picture, it’s the bug’s center that we’ve positioned at (100,300). Had we used the coordinates (0,0) instead, just the bottom right-hand corner of the bug would have appeared at the top-left corner of the background. (Try it!) It’s as if there’s a pin at the center of the bug that it attaches with. We won’t call it a pin, though, but an anchor:
bug.anchorres20: Anchor = Center
Each Pic object attaches at a particular
point, which we can access through the
object’s anchor variable.
Unless otherwise specified, a picture’s
anchor is the middle point between its most
extreme coordinates, here described as Center.
Package o1 represents anchors with a custom
data type Anchor.
In many cases, an anchor at the center is what we want, but it’s also common that another option is more convenient. There are many alternatives for anchoring a picture. Let’s explore:
show(sky.place(bug, Center, Pos(0, 0)))
The second parameter is of type Anchor
and tells the method that it’s the bug’s
center that we wish to place at (0,0).
Notice that this value is not a string
and therefore is not in quotation marks.
The command above does the same thing we did before, anchoring the Pic at its center,
but it also reveals how we can change the anchoring point. Try these:
show(sky.place(bug, TopLeft, Pos(0, 0)))show(sky.place(bug, CenterLeft, Pos(0, 0)))
How about the next place command? Why doesn’t it “do anything”?
show(sky.place(bug, TopRight, Pos(0, 0)))
Hare are some anchors you can use: TopLeft, TopCenter, TopRight, CenterLeft,
Center, CenterRight, BottomLeft, BottomCenter, BottomRight.
Anchoring onto an anchor
In the examples above, we used absolute coordinates such as (0,0) to specify the background location where the anchor is positioned. In the example below, too, we use the coordinates (100,225) in this manner.
val trunk = rectangle(30, 250, SaddleBrown)
val foliage = circle(200, ForestGreen)
val tree = trunk.onto(foliage, Pos(100, 225))
The numbers in the example aren’t arbitrary. They’ve been carefully chosen:
100 is at the center of the foliage.
225 is 125 pixels (i.e., half of the length of the trunk) lower than the center of the foliage.
By calculating these values outside the program itself, we’ve managed to place the middle point of the trunk’s top edge exactly at the center of the foliage. That took a bit of manual effort and, more importantly, if we change the size of the foliage or the trunk, we must remember and bother to recalculate the numbers. What’s more, anyone reading the program needs to reason about where those exact numbers came from.
Here’s a nicer version:
val trunk = rectangle(30, 250, SaddleBrown)
val foliage = circle(200, ForestGreen)
val tree = trunk.onto(foliage, TopCenter, Center)
We can use anchors to specify not only a spot in the picture being placed (the top center of the trunk) but also the target spot in the background image (the center of the foliage).
Finally, see below for a slightly longer example that uses these methods to form a scenery that’s made up of sky, ground, a tree, and a bug. Read the code, try to predict what the combined picture will be like, and run the code to see if you were right.
val sky = rectangle(1000, 400, LightBlue)
val ground = rectangle(1000, 50, SandyBrown)
val bug = Pic("ladybug.png")
val trunk = rectangle(30, 250, SaddleBrown)
val foliage = circle(200, ForestGreen)
val tree = trunk.onto(foliage, TopCenter, Center)
val rootedTree = tree.onto(ground, BottomCenter, Pos(500, 30))
val scenery = sky.place(rootedTree, BottomLeft, BottomLeft).place(bug, Pos(100, 300))
An exercise in anchoring

Write an effect-free function named flagOfCzechia that:
receives as its only parameter a width as a
Double; andreturns a
Picof the national flag of Czechia, whose:width is determined by the parameter;
height is two thirds of the width;
left edge contains an isosceles triangle whose apex just reaches the flag’s center; and
whose colors are
MidnightBlue,White, andCrimson.
You can use an expression of the form triangle(width, height, color)
to create a triangle. Such a triangle has its base at the bottom edge
and the equally long sides on the left and the right.
It’s possible to solve the assignment without anchors but this is a good opportunity to put them to use. Put them to use. Can you come up with multiple ways of anchoring the triangle in the flag?
Write this function, too, in week2.scala.
A+ presents the exercise submission form here.
Summary of Key Points
By defining methods on a class, you can establish a set of rules that governs how the values of a particular type — the instances of the class — may be combined to produce new instances.
In O1,
Pos,Odds, andPicare examples of classes in this vein.Cf. the mathematical rules for applying operators to numbers, producing new numbers.
Programmers sometimes use pseudocode — text that resembles program code — for sketching out solutions, among other things.
You can include a method named
toStringin a Scala class. This method returns a string description of the object.toStringmethods can be convenient when testing the class, for example.The class
Pos, provided as part of packageo1, represents pairs of coordinates. You can use it in combination with classPicfor a variety of image manipulations.Links to the glossary: class, instance, reference; pseudocode;
toString, to override; anchor.
Feedback
Please note that this section must be completed individually. Even if you worked on this chapter with a pair, each of you should submit the form separately.
Credits
Thousands of students have given feedback and so contributed to this ebook’s design. Thank you!
The ebook’s chapters, programming assignments, and weekly bulletins have been written in Finnish and translated into English by Juha Sorva.
The appendices (glossary, Scala reference, FAQ, etc.) are by Juha Sorva unless otherwise specified on the page.
The automatic assessment of the assignments has been developed by: (in alphabetical order) Riku Autio, Nikolas Drosdek, Kaisa Ek, Joonatan Honkamaa, Antti Immonen, Jaakko Kantojärvi, Niklas Kröger, Kalle Laitinen, Teemu Lehtinen, Mikael Lenander, Ilona Ma, Jaakko Nakaza, Strasdosky Otewa, Timi Seppälä, Teemu Sirkiä, Anna Valldeoriola Cardó, and Aleksi Vartiainen.
The illustrations at the top of each chapter, and the similar drawings elsewhere in the ebook, are the work of Christina Lassheikki.
The animations that detail the execution Scala programs have been designed by Juha Sorva and Teemu Sirkiä. Teemu Sirkiä and Riku Autio did the technical implementation, relying on Teemu’s Jsvee and Kelmu toolkits.
The other diagrams and interactive presentations in the ebook are by Juha Sorva.
The O1Library software has been developed by Aleksi Lukkarinen and Juha Sorva. Several of its key components are built upon Aleksi’s SMCL library.
The pedagogy of using O1Library for simple graphical programming (such as Pic) is
inspired by the textbooks How to Design Programs by Flatt, Felleisen, Findler, and
Krishnamurthi and Picturing Programs by Stephen Bloch.
The course platform A+ was originally created at Aalto’s LeTech research group as a student project. The open-source project is now shepherded by the Computer Science department’s edu-tech team and hosted by the department’s IT services. Markku Riekkinen is the current lead developer; dozens of Aalto students and others have also contributed.
The A+ Courses plugin, which supports A+ and O1 in IntelliJ IDEA, is another open-source project. It has been designed and implemented by various students in collaboration with O1’s teachers.
For O1’s current teaching staff, please see Chapter 1.1.
Additional credits for this page
MAD fold-ins are the work of the late Al Jaffee.
The clownified painting is The Defense of the Sampo by Akseli Gallén-Kallela.
We create a new
Posobject to represent the new position.