1. CS-A1110
  2. Kierros 10
  3. Luku 10.1: Vertaillaan, järjestellään ja ryhmitellään

Luku 10.1: Vertaillaan, järjestellään ja ryhmitellään

../_images/person11.png

Johdanto

Olet nähnyt useita esimerkkejä yleisestä ohjelmoijan tarpeesta: on etsittävä luvuista, merkkijonoista tai muista olioista se, joka on suurin, pienin, paras, huonoin tai muuten sopivin jonkin kriteerin perusteella.

Toinen yleinen tarve on arvojen järjestäminen jonkin kriteerin perusteella, esimerkiksi suurimmasta pienimpään tai toisinpäin. Jos mietit vaikkapa yleisiä käyttämiäsi sovelluksia ja web-palveluita, keksit varmasti heti itsekin tilanteita, joissa järjestämisestä on hyötyä.

Sekä sopivimman arvon etsimiselle että järjestämiselle on ominaista, että arvoja on vertailtava jollakin kriteerillä. Siksi aloitamme tämän luvun pohtimalla erilaisia vertailutapoja.

Käymme jälleen Scala APIn työkalupakilla.

Kuten jo tiedät:

Kurssin tarkoituksena ei ole kahlata läpi koko Scala APIa vaan poimia sieltä ohjelmoinnin perusteiden kannalta opettavaisia osia. Tässäkin luvussa käsitellään vain osa Scala APIn runsaasta valikoimasta vertailemiseen ja järjestämiseen sopivia työkaluja.

Arvojen vertaileminen "luonnollisesti"

Aloitetaan tutkimalla konkreettista koodia.

Kokoelmien max- ja min-metodit

Kokoelmilla on max-niminen metodi, joka etsii ja palauttaa suurimman alkion. Kun kyseessä ovat lukualkiot, suurin alkio määräytyy luonnolliseen tapaan:

Vector(3, 5, -50, 20, 1, 5).maxres0: Int = 20

Joissakin aiemmissa luvuissa olemme vertailleet merkkijonoja Unicode-aakkoston mukaan. Samaan nojautuu myös max, joka palauttaa aakkosissa viimeisen merkkijonon kokoelmasta:

Vector("a", "bb", "b", "abc", "ba").maxres1: String = bb

min-metodi toimii aivan vastaavasti. Sillä voi selvittää esimerkiksi vektorin pienimmän luvun tai aakkosissa ensimmäisen merkkijonon.

Luonnollinen järjestys

Luvuilla ja merkkijonoilla on ns. luonnollinen järjestys, johon min- ja max-metodit perustuvat. Asiaa voi ajatella vaikka näin: jos arvo ei ole isompi tai pienempi kuin toinen, niin onko kyseessä sama arvo? Tämähän pätee esimerkiksi kokonaisluvuille, kun niitä vertaillaan keskenään suuremmuuden mukaan: jos luku ei ole isompi tai pienempi, niin kyseessä on sama lukuarvo. Sama pätee merkkijonoille aakkosjärjestyksen mukaan vertaillessa.

Luonnollisella järjestyksellä siis viitataan siihen, että arvojen järjestys on kahlittu siihen, mistä nimenomaisesta arvosta on kysymys.

Esimerkki ei-luonnollisesta järjestyksestä on merkkijonojen järjestäminen pituuden mukaan: kaksi samanmittaista merkkijonoa eivät suinkaan välttämättä ole sama merkkijono. Toinen esimerkki on GoodStuff-ohjelmasta tuttu kokemusolioiden vertailu arvosanan mukaan. Vaikka kokemuksilla on sama arvosana, eivät ne välttämättä ole sama kokemus.

Ordered-piirreluokka

Luonnollinenkin järjestys täytyy tietysti määritellä tietokoneelle. Scalassa tämä on tehty määrittelemällä Ordered-piirreluokka. Se edustaa keskenään luonnollisella tavalla vertailukelpoisia olioita. Monet Scalan valmiit tietotyypit perivät Ordered-piirteen; näihin kuuluvat esimerkiksi Int, Double, merkkijonot ja totuusarvot. (Myös itse määrittelemäsi luokat voivat periä Ordered-piirteen, mutta sitä emme tee tällä kurssilla.)

Ordered-piirreluokassa on abstrakti metodi, joka määrittelee sen perusteen, jolla arvoja vertaillaan. Konkreettiset tietotyypit toteuttavat tämän metodin kukin omalla tavallaan. Esimerkiksi kokonaisluvuille se on toteutettu lukujen suuremmuusvertailuna ja merkkijonoille aakkosvertailuna.

Tärkein hyöty Ordered-piirreluokasta on, että se toimii yläkäsitteenä kaikille sellaisille tietotyypeille, joilla on luonnollinen järjestys. Niinpä voidaan määritellä metodeita, jotka käsittelevät Ordered-tyyppisiä arvoja ja siis toimivat kaikenlaisille olioille, joita voi vertailla luonnollisesti keskenään: kokonaisluvuille, desimaaliluvuille, merkkijonoille jne.

Tätä potentiaalia onkin hyödynnetty Scalan ohjelmakirjastoissa. Alkiokokoelmia kuvaavilla luokilla on metodeita, jotka toimivat Ordered-tyyppisille alkioille. Yllä esitellyt max ja min toimivat kuvatulla tavalla vain silloin, kun kokoelman alkiot ovat luonnollisesti järjestettävissä. Esimerkiksi Pos-oliot eivät ole:

Vector(Pos(10, 5), Pos(7, 12)).max-- Error: ... No implicit Ordering defined for B
  |where:    B is a type variable with constraint >: o1.world.Pos

Alkioiden luonnollista järjestystä hyödynnämme myös seuraavaksi, kun kokeilemme kokoelman järjestämistä.

Kokoelman järjestäminen: sorted

sorted-metodi järjestää alkiot — joiden tulee olla keskenään vertailukelpoisia — kasvavaan järjestykseen:

Vector(3, 5, -50, 20, 1, 5).sortedres2: Vector[Int] = Vector(-50, 1, 3, 5, 5, 20)
Vector("a", "bb", "b", "abc", "ba").sortedres3: Vector[String] = Vector(a, abc, b, ba, bb)

sorted-metodi palauttaa uuden kokoelman, jossa samat alkiot ovat eri järjestyksessä. Se ei muuta alkuperäistä kokoelmaa. Vektoriahan ei edes voisi muuttaa.

Jos haluamme päinvastaisen tuloksen, voimme esimerkiksi käyttää reverse-metodia (luvusta 4.2):

Vector(3, 5, -50, 20, 1, 5).sorted.reverseres4: Vector[Int] = Vector(20, 5, 5, 3, 1, -50)

Miten järjestäminen toimii?

Järjestämisalgoritmit eli lajittelualgoritmit (sorting algoritms) ovat klassinen algoritmitutkimuksen ala. On kehitetty paljon tehokkuusominaisuuksiltaan toisistaan poikkeavia järjestämisalgoritmeja.

Myös Scala API tarjoaa valikoiman erilaisia toteutuksia järjestämiselle. Toteutuksiin ei kuitenkaan tutustuta tällä kurssilla. Nyt riittää, että käytät tiettyjä valmiiksi määriteltyjä järjestämismetodeita.

Jos haluat, voit miettiä, miten toteuttaisit itse funktion, joka järjestää vaikkapa parametriksi annetun kokonaislukuja sisältävän puskurin.

Internetistä löytyy yllin kyllin lisätietoa järjestämisestä. Aihetta käsitellään myös Aallon jatkokursseilla.

Vertaileminen mielivaltaisella kriteerillä

Metodit max, min ja sorted toimivat somasti, kun alkioilla on luonnollinen järjestys.

Vaan entä jos alkiotyypillä ei olekaan piirrettä Ordered? Ehkä haluamme vaikkapa etsiä Shape-tyyppisistä kuvio-olioista pinta-alan mukaan suurimman.

Ja vaikka Ordered-piirre olisikin, saatamme haluta luonnollisen järjestyksen sijaan jonkin muun. Ehkä haluamme vaikkapa etsiä merkkijonoista lyhimmän eikä aakkosissa ensimmäisen.

Tuollaisiin tarpeisiin vastaavat näppärästi metodit maxBy, minBy ja sortBy, joista on esimerkkejä alla.

Seuraavissa esimerkeissä käytetään alkioina merkkijonojen ja kokonaislukujen lisäksi kuvio-olioita (luvusta 7.3). Tässä pikakertaus kuvioluokkien oleellisista osista:

trait Shape:
  def area: Double
  // ...

class Circle(val radius: Double) extends Shape:
  def area = math.Pi * this.radius * this.radius
  // ...

class Rectangle(val sideLength: Double, val anotherSideLength: Double) extends Shape:
  def area = this.sideLength * this.anotherSideLength
  // ...

(Lisäksi näihin luokkiin on laadittu toString-metodit, jotta tulosteet REPLissä ovat selkeämmät.)

maxBy- ja minBy-metodit

Tässä etsitään pisin merkkijono ja neliöltään suurin luku:

Vector("a", "bb", "b", "abc", "ba").maxBy( _.length )res5: String = abc
Vector(3, 5, -50, 20, 1, 5).maxBy( math.pow(_, 2) )res6: Int = -50

Ajatuksena on siis, että maxBy-metodille annetaan parametriksi funktio, jota kutsutaan kullekin alkiolle. Funktion paluuarvojen täytyy olla keskenään vertailukelpoisia, kuten esimerkiksi jonojen pituudet ja lukujen toiset potenssit ovat. Metodi määrittää suurimman arvon näiden paluuarvojen eikä alkuperäisten alkioiden perusteella.

maxBy-toimii luonnollisesta järjestyksestä riippumattomasti ja siis myös, vaikkei alkiolla luonnollista järjestystä olisikaan. Shape-oliot eivät peri Ordered-piirrettä laisinkaan, mutta pinta-alaltaan suurimman kuvion etsiminen sujuu helposti:

val kuvioita = Vector(Circle(5), Rectangle(5, 11), Rectangle(30, 5))kuvioita: Vector[Shape] = Vector(CIRC[ r=5.0 a=78.54 ], RECT[ 5.0*11.0 a=55.0 ], RECT[ 30.0*5.0 a=150.0 ])
kuvioita.maxBy( _.area )res7: Shape = RECT[ 30.0*5.0 a=150.0 ]

minBy toimii vastaavasti.

Entä jos alkioita ei ole? (maxByOption jne.)

Tässä yksi tapa toteuttaa GoodStuff-ohjelman Category-luokan suosikkiuskirjanpito, jota on versioitu pitkin kurssia:

def favorite = if this.experiences.isEmpty then None else Some(this.experiences.maxBy( _.rating ))

Jos kokemuksia ei ole, ei ole suosikkiakaan.

Muuten suosikki on tämän kategorian kokemuksista se, joka on arvosanaltaan suurin.

Tuo on esimerkki monissa ohjelmissa toistuvasta tarpeesta: halutaan isoin alkio tai None, jos alkioita ei ole. Niinpä siihen on räätälöity metodi, maxByOption. Tämä tekee ihan saman kuin äskeinen koodi:

def favorite = this.experiences.maxByOption( _.rating )

Vastaavasti on olemassa metodi minByOption sekä luonnolliseen järjestykseen perustuvat maxOption ja minOption.

sortBy-metodi

sortBy-metodi on samansuuntainen. Esimerkiksi merkkijonot voi järjestää pituuden perusteella, luvut toisen potenssin perusteella ja kuviot pinta-alan perusteella:

Vector("a", "bb", "b", "abc", "ba").sortBy( _.length )res8: Vector[String] = Vector(a, b, bb, ba, abc)
Vector(3, 5, -50, 20, 1, 5).sortBy( math.pow(_, 2) )res9: Vector[Int] = Vector(1, 3, 5, 5, 20, -50)
Vector(Circle(5), Rectangle(5, 11), Rectangle(30, 5)).sortBy( _.area )res10: Vector[Double] = Vector(RECT[ 5.0*11.0 a=55.0 ], CIRC[ r=5.0 a=78.54 ], RECT[ 30.0*5.0 a=150.0 ])

sortBy-metodilla voi tuottaa myös käänteisen normaalijärjestyksen (vrt. reverse edellä). Tässä ensin pidempi ja sitten lyhyempi versio:

Vector(3, 5, -50, 20, 1, 5).sortBy( n => -n )res11: Vector[Int] = Vector(20, 5, 5, 3, 1, -50)
Vector(3, 5, -50, 20, 1, 5).sortBy( -_ )res12: Vector[Int] = Vector(20, 5, 5, 3, 1, -50)

Käänteinen tulos saatiin järjestämällä luvut niiden itsensä sijaan niiden vastalukujen perusteella.

Tähtikarttatehtävä, osa 4/4: tähtikuvioita (B45)

Luvussa 4.4 tutustuit Stars-ohjelmaan. Luvussa 5.2 saimme taivaan tähdet näkyviin. Täydennetään nyt ohjelmaa piirtämällä taivaalle myös tähtikuvioita.

Tehtävänanto

Tutustu luokan Constellation dokumentaatioon ja puutteelliseen koodiin. Huomaa erityisesti:

  • Koodista puuttuvat stars, minCoords ja maxCoords.

  • Tähtikuvio rakennetaan vektorillisesta pareja.

  • Muuttujan stars tyyppi on Set[Star] eli joukko tähtiä.

    • Joukko on alkiokokoelma. Toisin kuin esimerkiksi vektorissa tai puskurissa, joukossa ei voi koskaan olla useita kopioita samasta arvosta.

    • Joukon alkioilla ei myöskään ole järjestysnumeroita (indeksejä).

    • Joukon voi muodostaa toSet-metodikutsulla (esim. vektori.toSet). Jos alkuperäisessä kokoelmassa oli sama arvo useasti, syntyvässä joukossa se on silti vain kerran.

Täydennä ohjelma:

  1. Ohjelma tuntee muutaman tähtikuvion, jotka on määritetty northern-kansiossa. Muuttujan starDataFolder arvo pitää olla gui/StarryApp.scalassa kunnossa, jotta tähdet (ja myöhemmin kuviot) tulevat näkyviin. Varmista aluksi, että näin on.

  2. Toteuta luokka Constellation dokumentaation mukaiseksi.

  3. Toteuta myös gui/skypics.scalasta puuttuva funktio placeConstellation.

  4. Muokkaa skypics.scalan createSkyPic-funktiota niin, että se lisää palauttamaansa kuvaan (tähtien päälle) myös StarMap-parametrinsa tähtikuviot.

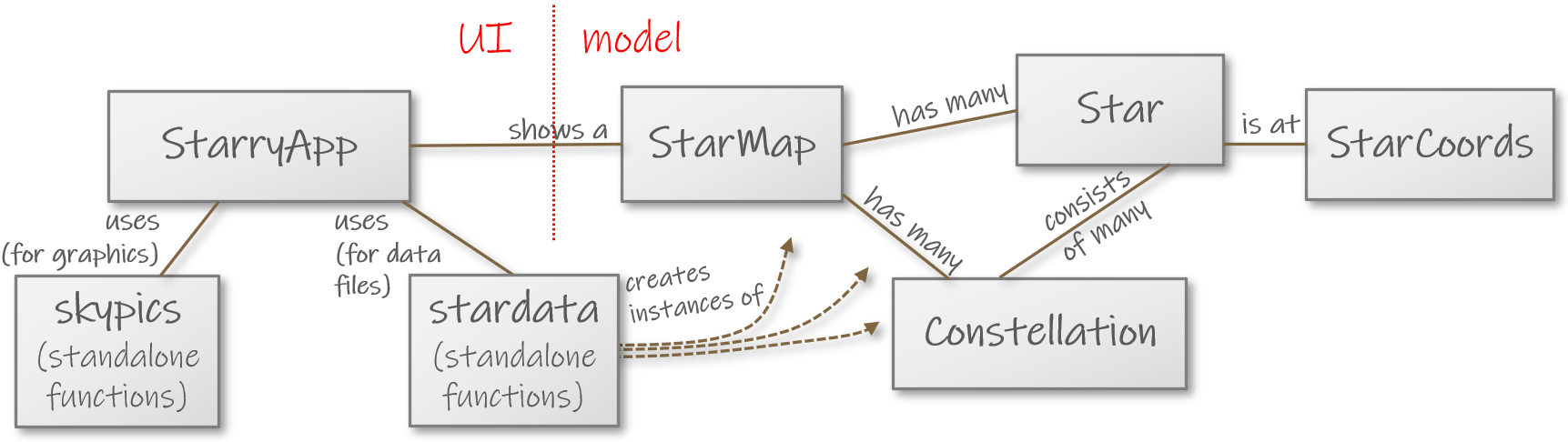
../_images/module_stars_withconstellations.png

Kaavio Stars-ohjelman rakenteesta.

Suositellut työvaiheet ja vinkkejä

  1. Toteuta muuttuja stars luokkaan Constellation. Mahdollisia työvälineitä:

    • ++ (luku 4.2)

    • unzip (luku 9.2)

    • toSet (yllä)

  2. Toteuta samaan luokkaan minCoords ja maxCoords. Käytä tämän luvun esittelemiä metodeita.

  3. Aja ohjelma. Tähtikuviot eivät vielä piirry, mutta eräiden tähtikuvioiden nimien pitäisi tulla tekstinä näkyviin, kun siirtelet hiiren kursoria kuvan päällä.

    • Annettu käyttöliittymä lisää nuo tekstit, jos kursori on tähtikuvion minCoordsin ja maxCoordsin välisellä alueella.

  4. Täydennä placeConstellation-funktio skypics.scalaan.

    • Voit kutsua Pic-luokan place-metodia aiempaankin tyyliin. Toisaalta tuosta metodista on myös versio, jolle voi antaa parametreiksi pareja, ja jota ehkä haluat kokeilla. Tähän tapaan:

      taustakuva.place(kuva1 -> sijainti1, kuva2 -> sijainti2, kuva3 -> sijainti3)

    • Viivan kuvan saa aikaan helposti line-metodilla. Tuo metodi on aiemmin mainittu vain luvun 3.1 valinnaisessa materiaalissa, mutta sen käyttö on helppoa. Tässä pikkuesimerkki:

      val viiva = line(Pos(0, 0), Pos(150, 100), Red)viiva: Pic = line-shape

      Kun lisäät viivan kuvaan place-metodilla tiettyihin Pos-koordinaatteihin, tulee kyseiseen kohtaan viivan alkupää (ei keskikohta).

    • foldLeft-metodi (luku 7.1) on tässä kätevä: tarkoitushan on koostaa kuva useasta kuvasta. for-silmukallakin pärjää.

  5. Täydennä createSkyPic lisäämään myös tähtikuviot.

  6. Kuvioiden pitäisi nyt piirtyä näkyviin, kun ajat ohjelman.

    • Jos eivät näy, varmista vielä, että sinulla on StarryApp.scalassa valittuna kartaksi "northern" eikä "test".

A+ esittää tässä kohdassa tehtävän palautuslomakkeen.

Hakurakenteen luominen olemassa olevasta datasta: toMap

Usein haluamme luoda hakurakenteen olemassa olevista olioista niin, että tietty noiden olioiden ominaisuus toimii avaimena.

Esimerkin johdanto

Käytetään tätä Member-luokkaa:

class Member(val id: Int, val name: String, val yearOfBirth: Int, val yearOfDeath: Option[Int]):
  override def toString = this.name + "(" + this.yearOfBirth + "-" + this.yearOfDeath.getOrElse("") + ")"

Sanotaan vielä, että meillä on käytössä luettelo jäsentietoja vektorissa. Tässä esimerkissä tiedot syötetään REPLissä, mutta ne olisi voitu lukea vaikkapa jostakin tallennetusta tiedostosta:

val jasenluettelo = Vector(Member(123, "Madonna", 1958, None),
                           Member(321, "Elvis", 1935, Some(1977)),
                           Member(555, "Michelangelo", 1475, Some(1564)))jasenluettelo: Vector[Member] = Vector(Madonna(1958-), Elvis(1935-1977), Michelangelo(1475-1564))

Miten saisimme tämän vektorin perusteella helposti luotua hakurakenteen, josta jäseniä voi poimia jäsennumeron perusteella ja jossa olisi vektorin sisältö?

Pohjustusvaihe: pareja vektoriin

Ensinnäkin on pystyttävä muodostamaan avain–arvo-pareja, joissa avaimina on jäsennumerot ja arvoina jäsenoliot.

jasenluettelo.map( jasen => jasen.id -> jasen )res13: Vector[(Int, Member)] = Vector((123,Madonna(1958-)), (321,Elvis(1935-1977)), (555,Michelangelo(1475-1564)))

Metodille map annetaan nimetön funktio, joka ottaa parametrikseen jäsenolion, ja...

... muodostaa tuota oliota vastaavan avain–arvo-parin. Tämän lausekkeen ympärille voisi lisätä selkiyttävät sulkeet.

Parit hakurakenteeksi toMap-metodilla

Äsken syntyi siis vektorillinen avain–arvo-pareja. Näistä pareista voi muodostaa Map-olion vaivattomasti toMap-metodilla. Lisätään vain toMap-kutsu edellisen lausekkeen perään:

val jasenhakemisto = jasenluettelo.map( jasen => jasen.id -> jasen ).toMapjasenhakemisto: Map[Int,Member] = Map(123 -> Madonna(1958-),
                                      321 -> Elvis(1935-1977),
                                      555 -> Michelangelo(1475-1564))
jasenhakemisto.get(321)res14: Option[Member] = Some(Elvis(1935-1977))

toMap-metodi toimii mielekkäästi, kunhan kokoelma sisältää avain–arvo-pareja ja kukin avain on erilainen kuin toiset (kuten jäsennumerot yllä ovat).

toMap-metodin synnyttämä uusi hakurakenne on tilaltaan muuttumaton.

zip plus toMap

zip-metodi (luku 9.2) on usein kätevä hakurakenteita muodostaessa. Tässä pieni esimerkki, jossa hakurakenne muodostetaan kahdesta erillisestä olemassa olevasta vektorista, joista toisessa on avaimet (lajien nimet) ja toisessa niitä vastaavat arvot (korkeudet sentteinä):

val elaimet = Vector("laama", "alpakka", "vikunja")elaimet: Vector[String] = Vector(laama, alpakka, vikunja)
val korkeudet = Vector(120, 90, 80)korkeudet: Vector[Int] = Vector(120, 90, 80)

Yhdistetään kokoelmat zip-metodilla pareja sisältäväksi vektoriksi, niin voimme kutsua toMap-metodia:

val korkeushakemisto = elaimet.zip(korkeudet).toMapkorkeushakemisto: Map[String,Int] = Map(laama -> 120, alpakka -> 90, vikunja -> 80)
korkeushakemisto.get("alpakka")res15: Option[Int] = Some(90)

Myös jäsenesimerkissä olisimme voineet käyttää zip-metodia ja korvata tämän:

jasenluettelo.map( jasen => jasen.id -> jasen )

tällä saman asian hoitavalla koodilla:

jasenluettelo.map( _.id ).zip(jasenluettelo)

Hakurakenteen luominen olemassa olevasta datasta: groupBy

Nähdyssä esimerkissä käytimme avaimena jäsennumeroa, joka on kullakin jäsenellä eri luku. Voimme myös käyttää avaimena sellaista ominaisuutta, joka ei ole oliolle ainutlaatuinen. Toisin sanoen: voimme ryhmitellä olioita tietyn kriteerin perusteella.

Tällaiseen tarpeeseen sopii metodi groupBy. Samassa hengessä kuin metodeille sortBy, maxBy ja minBy, myös tälle metodille välitetään parametriksi funktio, jota se käyttää arvojen keskinäiseen vertailemiseen. Ryhmitellään jäsenemme vaikkapa syntymävuosisadan perusteella:

jasenluettelo.groupBy( _.yearOfBirth / 100 )res16: Map[Int,Vector[Member]] = Map(14 -> Vector(Michelangelo(1475-1564)),
                                     19 -> Vector(Madonna(1958-), Elvis(1935-1977)))

Huomion voi kiinnittää ensin hakurakenteen tyyppiin. Tässä luodaan hakurakenne, jossa kunkin kokonaislukuavaimen "takana" on vektorillinen jäseniä.

Esimerkiksi: avain 19 kuvaa 1900-lukua. Sen takana on vektori, jossa on kaikki 1900-luvulla syntyneet jäsenet. Niitä on tässä esimerkkidatassa kaksi.

Tällainen kokoelma on saatu luotua groupBy-kutsulla, jolle on annettu parametriksi jäsenen syntymävuosisadan selvittävä pikkufunktio. groupBy-metodi kutsuu tätä funktiota jokaiselle jäsenelle jäsenluettelossa. Se luo ja palauttaa hakurakenteen, jossa...

... avaimina ovat kaikki eri arvot, jotka parametrifunktiota kutsumalla saatiin eli kaikki eri syntymävuosisadat ja...

... arvoina kokoelmat (tässä vektorit, koska alkuperäinen jäsenluettelokin on vektori), joihin jäsenet on ryhmitelty sen mukaan, mikä arvo niille saatiin parametrifunktiota kutsumalla.

partition ja groupBy

Luku 9.2 esitteli partition-metodin, jolla saatoimme esimerkiksi ryhmitellä lämpötilat negatiivisiin ja ei-negatiivisiin. Tuo metodi sopii tilanteisiin, joissa jaetaan tasan kahteen ryhmään Boolean-arvon palauttavan funktion perusteella. Kun tilanne ei ole niin yksinkertainen, on groupBy avuksi.

Myös groupBy-metodin luoma uusi hakurakenne on tilaltaan muuttumaton.

Tehtävä: monenlaisia kaupunkilaisia simulaattorissa (C4)

Luvussa 8.4 toteutit kaupunkisimulaattorin, jossa oli kaksi kansanosaa, sininen ja punainen (esimerkkiratkaisu). Muokataan simulaattoria niin, että kansanosia voi olla useampia.

../_images/schelling2.png

Päivitetty kaupunkisimulaattori on monivärisempi.

Tehtävänanto

Tämä muutos ei vaadi sinulta paljon: täydennä vain Simulator-luokkaan metodi residents. Se käy helposti, kun käytät groupBy-metodia ja CityMap-luokkaa.

Annettu käyttöliittymä huomioi tekemäsi muutoksen automaattisesti ja osaa piirtää erivärisiä ruutuja kartalle, kun ajat ohjelman.

A+ esittää tässä kohdassa tehtävän palautuslomakkeen.

Esimerkki: ohjaajatilastot

Johdanto

Yksi melko tyypillinen käyttötarkoitus hakurakenteille on esiintymien laskeminen.

Palataan suosittujen ohjaajien teemaan ja selvitetään hakurakenteen avulla, kuinka monta elokuvaa kullakin ohjaajalla on parhaimpien elokuvien luettelossa. Pistetään vielä ohjaajat tämän kriteerin mukaan järjestykseen. (Luvussa 1.6 käytit valmiina annettua funktiota samantapaiseen tarkoitukseen.)

Seuraava ohjelmakoodi löytyy myös kurssin oheismoduulista MovieStats.

Olkoon käytössä luokka Movie, joka kuvaa yhtä merkintää parhaiden elokuvien luettelossa. Se on yksinkertainen:

class Movie(val name: String, val year: Int, val position: Int,
            val rating: Double, val directors: Vector[String]):
  override def toString = this.name

Lisäksi käytämme luokkaa MovieListFile, joka osaa lukea ja jäsentää tietyssä muodossa olevia tekstitiedostoja. Siitä ei tarvitse nyt tietää muuta kuin sen käyttötapa:

val movieFile = MovieListFile("omdb_movies_2015.txt")movieFile: MovieListFile = omdb_movies_2015.txt (contains: 250 movies)
val allMovies = movieFile.moviesallMovies: Vector[o1.movies.Movie] = Vector(Das Boot, Amadeus, Heat, The Secret in Their Eyes, ...

Esiintymien laskeminen hakurakenteella

Miten saataisiin kunkin ohjaajan yleisyys luettelossa?

Ennen kuin ohjaajien esiintymät lasketaan, on järkevää muodostaa luettelo kaikista ohjaajista.

Koska kullakin elokuvalla voi olla useita ohjaajia, ei pelkkä allMovies.map( _.directors ) tuota haluttua tulosta (vaan luettelon elokuvakohtaisista ohjaajaluetteloista). Käytetään mieluummin flatMapiä:

val allDirectors = allMovies.flatMap( _.directors )allDirectors: Vector[String] = Vector(Wolfgang Petersen, Milos Forman, Michael Mann, Juan José Campanella, ...

Otetaan tavoitteeksi muodostaa sellainen hakurakenne, jossa avaimina ovat ohjaajien nimet ja arvoina elokuvien lukumäärät. Yksi tapa päästä tähän tavoitteeseen on seuraava:

  1. Etsitään kunkin ohjaajan esiintymät vektorissa ryhmittelemällä vektorin sisältö ohjaajan nimen mukaan. Siis: "niputetaan" kaikki yhden ohjaajan esiintymät.

  2. Lasketaan muodostuneiden "nippujen" koot ja yhdistetään ne hakurakenteeseen, avaimena kyseisen ohjaajan nimi.

Ajatus selvinnee parhaiten REPListä:

val groupedByDirector = allDirectors.groupBy( dir => dir )groupedByDirector: Map[String,Vector[String]] = Map(Paul Thomas Anderson -> Vector(Paul Thomas Anderson),
Peter Weir -> Vector(Peter Weir), Wim Wenders -> Vector(Wim Wenders), Wolfgang Petersen -> Vector(Wolfgang Petersen),
Giuseppe Tornatore -> Vector(Giuseppe Tornatore), Robert Rossen -> Vector(Robert Rossen), Dean DeBlois ->
Vector(Dean DeBlois), Charles Chaplin -> Vector(Charles Chaplin, Charles Chaplin, Charles Chaplin, Charles Chaplin,
Charles Chaplin), Ridley Scott -> Vector(Ridley Scott, Ridley Scott, Ridley Scott), Sean Penn -> ...

Katsotaan ensin, mitä tuloksena saadaan: hakurakenne, jossa merkkijonoavainten (ohjaajien nimien) takana on vektoreita, joissa on myös merkkijonoja. Tarkemmin sanoen:

Kuhunkin vektoriin on koottu jokainen kyseisen ohjaajan esiintymä alkuperäisessä ohjaajaluettelossa. Esimerkiksi Chaplinilla on viisi elokuvaa luettelossa, joten hänen nimensä toistuu viidesti. (Useimmilla ohjaajilla on vain yksi, joten vektorikin on yksialkioinen.)

Tämä tulos saatiin pienellä groupBy-kutsulla, joka ryhmittelee alkuperäisessä vektorissa olleet ohjaajanimet niiden itsensä mukaan (niin hassulta kuin se saattaa kuulostaakin). Lisää tästä alla.

Muista: groupBy-metodi kutsuu parametrifunktiotaan ohjaajaluettelon jokaiselle merkkijonolle ja luo uuden "ryhmän" jokaiselle erilaiselle arvolle, joka parametrifunktiolta saadaan paluuarvona.

Käytetään siis ryhmittelyn perustana funktiota, joka palauttaa juuri sen merkkijonon, joka sille annetaan parametriksikin. Näin saadaan muodostettua ryhmä jokaiselle erilaiselle alkuperäisen kokoelman sisältämälle merkkijonolle.

Nyt olemme enää kukonaskelen päässä alkuperäisen ongelman ratkaisusta. groupBy-metodilla muodostetusta hakurakenteesta voi luoda ohjaajalaskurit helposti, kun käytämme vielä map-metodia (luku 9.2). Vaihdetaan vain kunkin nimen kohdalle tallennetun vektorin tilalle kyseisen vektorin koko:

val countsByDirector = groupedByDirector.map( (dir, movies) => dir -> movies.size )countsByDirector: Map[String,Int] = Map(Paul Thomas Anderson -> 1, Peter Weir -> 1, Wim Wenders -> 1,
Wolfgang Petersen -> 1, Giuseppe Tornatore -> 1, Robert Rossen -> 1, Dean DeBlois -> 1, Charles Chaplin -> 5,
Ridley Scott -> 3, Sean Penn -> 1, Danny Boyle -> 1, Gore Verbinski -> 1, Joel Coen -> 3, John Sturges -> 1, ...

Siistimmän tulosteen saamme vaikkapa näin:

countsByDirector.foreach(println)(Paul Thomas Anderson,1)
(Peter Weir,1)
(Wim Wenders,1)
(Wolfgang Petersen,1)
(Giuseppe Tornatore,1)
(Robert Rossen,1)
(Dean DeBlois,1)
(Charles Chaplin,5)
(Ridley Scott,3)
(Sean Penn,1)
(Danny Boyle,1)
...

Ohjaajat järjestykseen

Tehdään vielä luettelo ohjaajista sen mukaisessa järjestyksessä, montako elokuvaa heillä on kyseisessä luettelossa, suurimmasta lukumäärästä alkaen. Toisin sanoen: muodostetaan luettelo hakurakenteen avain–arvo-pareista arvojen mukaisessa käänteisessä numerojärjestyksessä.

Tarvitsemme järjestämismetodia.

Ensin on syytä ottaa käyttöön hakurakenteen sijaan kokoelma, jossa alkioilla on mielekäs järjestys. Hakurakenteessahan järjestys on toteutusriippuvainen, eikä rakennetta voi järjestää arvojen mukaan. Vektori taas kelpaa:

val directorCountPairs = countsByDirector.toVectordirectorCountPairs: Vector[(String, Int)] = Vector((Paul Thomas Anderson,1), (Peter Weir,1), (Wim Wenders,1),
(Wolfgang Petersen,1), (Giuseppe Tornatore,1), (Robert Rossen,1), (Dean DeBlois,1), (Charles Chaplin,5),
(Ridley Scott,3), (Sean Penn,1), (Danny Boyle,1), (Gore Verbinski,1), (Joel Coen,3), (John Sturges,1), ...

Nyt siis directorCountPairs-muuttuja sisältää viittauksen vektoriin, jossa on pareja. Ja ei kun järjestämään:

val directorsSorted = directorCountPairs.sortBy( (dir, count) => -count )directorsSorted: Vector[(String, Int)] = Vector((Alfred Hitchcock,8), (Stanley Kubrick,8),
(Martin Scorsese,7), (Christopher Nolan,7), (Quentin Tarantino,6), (Steven Spielberg,6), ...

Järjestämiskriteerinä käytetään kunkin parin jälkimmäisen osan (eli tässä leffamäärän) vastalukua.

Miinus kääntää järjestyksen. Ilman sitä ohjaajat saataisiin vähäelokuvaisimmasta alkaen.

Kaunistetaan tulostetta vähän.

for (director, count) <- directorsSorted do
  println(s"$director: $count movies")Alfred Hitchcock: 8 movies
Stanley Kubrick: 8 movies
Martin Scorsese: 7 movies
Christopher Nolan: 7 movies
Quentin Tarantino: 6 movies
Steven Spielberg: 6 movies
...

Käymme parit läpi näppärästi kirjoittamalla sulkeet for-silmukkaan (luku 9.2).

Pikkutehtävä: hakurakenteet ja alkioiden järjestys

Oletetaan jo suoritetuiksi seuraavat käskyt.

val lukuja = Vector(15, 7, 5, 27, 3, 8, 67, 28, 39, 15, 115, 23)
val vikanNumeronMukaan = lukuja.groupBy( _ % 10 )
val pieninRyhmaEnsin = vikanNumeronMukaan.toVector.sortBy( (nro, ryhma) => ryhma.size )

Ryhmitellään luvut niiden viimeisen numeron mukaan.

Järjestetään ryhmät sen mukaan, mikä viimeisistä numeroista on harvinaisin ja mikä yleisin.

Mitkä seuraavista väittämistä pitävät paikkansa? Tutki itse REPLissä tarpeen mukaan.

Tehtävä: Election-ohjelman parantelua (osa 1/2; B45)

Luvuissa 5.6, 6.3 ja 7.1 työstit Election-moduulia. Siitä jäi puuttumaan useita metodeita, jotka toteutetaan tässä ja seuraavassa tehtävässä.

Tehtävänanto

  1. Tutustu (taas) Election-ohjelman Scaladoc-dokumentaatioon. Luokkaan District on määritelty useita metodeita, joita et toteuttanut aiemmissa tehtävissä.

  2. Korvaa luvussa 5.6 tehty topCandidate-toteutus yksinkertaisemmalla.

  3. Täydennä puuttuvat metodit candidatesByParty, topCandidatesByParty ja votesByParty. Muut luokasta puuttuvat metodit toteutetaan tehtävän kakkosvaiheessa alla.

Ohjeita ja vinkkejä

  • Jos et tehnyt aiempien lukujen tehtäviä, tee ne tai käytä pohjana esimerkkiratkaisuja. Viimeistään nyt kannattaa tehdä myös luvussa 5.6 ehdotettu countVotes-apumetodi.

  • Tässä tehtävässä käytät tilaltaan muuttumattomia hakurakenteita, jotka ovat oletusarvoisesti käytössä ilman lisämäärittelyjä. Älä ota muuttuvatilaista Map-luokkaa käyttöön pakkauksesta scala.collection.mutable.

  • Uusien metodien toteutus sujuu luultavasti helpoimmin, kun teet sen tässä järjestyksessä: candidatesByParty, topCandidatesByParty ja viimeiseksi votesByParty. Hyödynnä aiemmin laatimiasi metodeita mahdollisuuksien mukaan.

  • Hyötyä on paitsi tässä luvussa esitellystä metodista ja muistakin kokoelmien metodeista. Kun valitset sopivat työkalut, ei koodia tarvita kuin pieni määrä.

  • Testaa ratkaisuasi annetulla testElection-ohjelmalla. Löydät tähän tehtävään liittyvän osion test.scalan lopusta. Poista kommenttimerkit osion ympäriltä.

A+ esittää tässä kohdassa tehtävän palautuslomakkeen.

Tehtävä: Election-ohjelman parantelua (osa 2/2; C40)

Tehtävänanto

Toteuta vielä puuttuvat District-luokan metodit:

  1. rankingsWithinParties

  2. rankingOfParties

  3. distributionFigures

  4. electedCandidates

Ohjeita ja vinkkejä

  • Kannattanee toteuttaa metodit yllä luetellussa järjestyksessä. Hyödynnä aiemmin laatimiasi metodeita mahdollisuuksien mukaan.

  • Inspiraatiota voit hakea tämän ja edellisten lukujen esimerkeistä, etenkin yllä olevasta ohjaajatilastoesimerkistä.

  • Vaihda hakurakenne vektoriksi (toVector) ja vektori hakurakenteeksi (toMap) tarvittaessa.

    • Jos alkiot eivät pysy järjestyksessä, pikkutehtävän kertaaminen tuosta yltä voi auttaa.

  • Tämä tehtävä on yksi tilaisuus kokeilla paikallisen funktion (luku 7.1) määrittelemistä metodin sisään. Voit siis kirjoittaa defin defin sisään.

    • Voisiko esimerkiksi yksittäisen ehdokkaan vertailuluvun määrittelemisestä tehdä oman apufunktionsa distributionFigures-metodin sisään?

A+ esittää tässä kohdassa tehtävän palautuslomakkeen.

Yhteenvetoa

  • Kokoelman alkioiden vertaileminen ja järjestäminen ovat ohjelmissa yleisiä.

  • Scala API tarjoaa monipuolisen metodivalikoiman "suurimpien" ja "pienimpien" etsimiseen sekä alkioiden järjestämiseen.

  • Hakurakenteita voi muodostaa muiden kokoelmien sisältämästä datasta, niiden alkioita ryhmitellen. Hakurakennetta voi näin käyttää muun muassa esiintymien laskemiseen.

Palaute

Huomaathan, että tämä on henkilökohtainen osio! Vaikka olisit tehnyt lukuun liittyvät tehtävät parin kanssa, täytä palautelomake itse.

Tekijät

Tämän oppimateriaalin kehitystyössä on käytetty apuna tuhansilta opiskelijoilta kerättyä palautetta. Kiitos!

Materiaalin luvut tehtävineen ja viikkokoosteineen on laatinut Juha Sorva.

Liitesivut (sanasto, Scala-kooste, usein kysytyt kysymykset jne.) on kirjoittanut Juha Sorva sikäli kuin sivulla ei ole toisin mainittu.

Tehtävien automaattisen arvioinnin ovat toteuttaneet: (aakkosjärjestyksessä) Riku Autio, Nikolas Drosdek, Kaisa Ek, Joonatan Honkamaa, Antti Immonen, Jaakko Kantojärvi, Onni Komulainen, Niklas Kröger, Kalle Laitinen, Teemu Lehtinen, Mikael Lenander, Ilona Ma, Jaakko Nakaza, Strasdosky Otewa, Timi Seppälä, Teemu Sirkiä, Joel Toppinen, Anna Valldeoriola Cardó ja Aleksi Vartiainen.

Lukujen alkuja koristavat kuvat ja muut vastaavat kuvituskuvat on piirtänyt Christina Lassheikki.

Yksityiskohtaiset animaatiot Scala-ohjelmien suorituksen vaiheista suunnittelivat Juha Sorva ja Teemu Sirkiä. Teemu Sirkiä ja Riku Autio toteuttivat ne apunaan Teemun aiemmin rakentamat työkalut Jsvee ja Kelmu.

Muut diagrammit ja materiaaliin upotetut vuorovaikutteiset esitykset laati Juha Sorva.

O1Library-ohjelmakirjaston ovat kehittäneet Aleksi Lukkarinen, Juha Sorva ja Jaakko Nakaza. Useat sen keskeisistä osista tukeutuvat Aleksin SMCL-kirjastoon.

Tapa, jolla käytämme O1Libraryn työkaluja (kuten Pic) yksinkertaiseen graafiseen ohjelmointiin, on saanut vaikutteita tekijöiden Flatt, Felleisen, Findler ja Krishnamurthi oppikirjasta How to Design Programs sekä Stephen Blochin oppikirjasta Picturing Programs.

Oppimisalusta A+ luotiin alun perin Aallon LeTech-tutkimusryhmässä pitkälti opiskelijavoimin. Nykyään tätä avoimen lähdekoodin projektia kehittää Tietotekniikan laitoksen opetusteknologiatiimi ja tarjoaa palveluna laitoksen IT-tuki; sitä ovat kehittäneet kymmenet Aallon opiskelijat ja muut.

A+ Courses -lisäosa, joka tukee A+:aa ja O1-kurssia IntelliJ-ohjelmointiympäristössä, on toinen avoin projekti. Sen suunnitteluun ja toteutukseen on osallistunut useita opiskelijoita yhteistyössä O1-kurssin opettajien kanssa.

Kurssin tämänhetkinen henkilökunta löytyy luvusta 1.1.

Lisäkiitokset tähän lukuun

Stars-ohjelma on mukaelma Karen Reidin suunnittelemasta ohjelmointiharjoituksesta. Se käyttää tähtidataa VizieR-palvelusta.

Thomas Schellingin laatimaan käyttäytymismalliin perustuva tehtävä on mukaelma Frank McCownin suunnittelemasta ohjelmointiharjoituksesta.

a drop of ink
Palautusta lähetetään...