1. CS-A1110
  2. Week 10
  3. Chapter 10.1: Comparing, Sorting, and Grouping

Luet oppimateriaalin englanninkielistä versiota. Mainitsit kuitenkin taustakyselyssä osaavasi suomea. Siksi suosittelemme, että käytät suomenkielistä versiota, joka on testatumpi ja hieman laajempi ja muutenkin mukava.

Suomenkielinen materiaali kyllä esittelee englanninkielisetkin termit.

Kieli vaihtuu A+:n sivujen yläreunan painikkeesta. Tai tästä: Vaihda suomeksi.


Chapter 10.1: Comparing, Sorting, and Grouping

../_images/person11.png

Introduction

You have already seen many examples of a common need: there is a bunch of numbers, strings, or other objects, and you need to find the one that is the greatest, least, longest, shortest, or otherwise best matches a particular criterion.

Another common need is to sort objects by a criterion, such as from the largest number to the smallest or vice versa. If you think about the most common applications and websites that you use, you will surely come up with any number uses for sorting.

In order to find the “best” element, we need to be able to compare elements; the same goes for sorting. Which is why we’ll start this chapter by considering comparisons.

We will again visit the Scala API for tools.

You know this already:

Our intention in O1 is not to wade through the entire Scala API but to highlight some parts of it that are useful for our purpose of learning the basics of programming. In this chapter, too, we’ll cover but a part of the API’s abundant selection of tools for comparing and sorting values.

Comparing Elements “Naturally”

Let’s start from a concrete example.

The methods max and min

Collections have a max method that seeks and returns the largest element. In the case of numerical elements, this means exactly what you think it means:

Vector(3, 5, -50, 20, 1, 5).maxres0: Int = 20

In some earlier chapters, we’ve compared strings by their characters’ position in the Unicode “alphabet”. That’s what max does, too, if you apply it to Stringss: you get the string that’s alphabetically last.

Vector("a", "bb", "b", "abc", "ba").maxres1: String = bb

min is analogous. You can use it to find, say, the smallest number in a vector or the alphabetically first string.

Natural ordering

Numbers and strings have a so-called natural ordering, which min and max rely on. Here’s how you can think about it: if each of two values is no more and no less than another, are they then the same value? Consider numbers, for instance: if an Int is not greater than another and not less than it either, you have two of the same number. The same goes for strings when you compare them alphabetically.

Natural ordering thus means that the ordering is innate to the values that are being ordered.

For an example of a non-natural ordering, consider sorting strings by their length: two strings of the same length aren’t necessarely the same string. Another example is from the GoodStuff program: even though two Experience objects have the same rating, they aren’t necessarily the same experience.

The Ordered trait

The computer needs a definition of any ordering we use, even a “natural” one. Scala gives us the Ordered trait, which is a supertype for any objects that have a natural ordering with respect to each other. Many of Scala’s built-in data types inherit this trait; these include Int, Double, String, Boolean, etc. (It’s also possible to write custom classes that inherit Ordered, but we’re not going to look into that now.)

The Ordered trait defines an abstract method that defines how values are compared. Concrete data types that inherit the trait implement the method in whichever way is appropriate for that type. On integers, the method is implemented as a numerical comparison, and on strings, as an alphabetical one.

The main benefit that we get from Ordered is that this type encompasses all the various data types that have a natural ordering. It thus becomes possible to define generic methods that operate on any values of type Ordered and therefore work on all objects that can be naturally compared to each other: integers, decimal numbers, strings, and so on.

The Scala API makes use of this potential. The collection classes of the API have several methods that work on elements of type Ordered. For example, max and min work as described above only if the elements have a natural ordering. Pos objects, for instance, do not:

Vector(Pos(10, 5), Pos(7, 12)).max-- Error: ... No implicit Ordering defined for B
  |where:    B is a type variable with constraint >: o1.world.Pos

We’ll also rely on natural ordering for our first efforts at sorting numbers, next.

Sorting a collection with sorted

The sorted method sorts the elements of a collection — which must be comparable with each other — in ascending order:

Vector(3, 5, -50, 20, 1, 5).sortedres2: Vector[Int] = Vector(-50, 1, 3, 5, 5, 20)
Vector("a", "bb", "b", "abc", "ba").sortedres3: Vector[String] = Vector(a, abc, b, ba, bb)

sorted returns a new collection with the elements in a new order. It doesn’t change the original collection. (Not that it’s even possible to change a Vector.)

If you want the reverse order, you can call reverse (introduced in Chapter 4.2):

Vector(3, 5, -50, 20, 1, 5).sorted.reverseres4: Vector[Int] = Vector(20, 5, 5, 3, 1, -50)

How does sorting work?

Sorting algorithms are a classic area of algorithms research. Computer scientists have come up with a variety of sorting algorithms that have different efficiency characteristics.

The Scala API also provides a number of implementations for sorting. We won’t study them in O1. For now, it’s enough that you can use some ready-made sorting methods.

As a voluntary exercise, you can think about how you might implement a function that sorts, say, a given buffer of integers.

You’ll find copious texts on sorting on the internet. O1’s follow-on courses at Aalto also discuss sorting.

Comparing Elements by Custom Criteria

max, min, and sorted work admirably as long as the elements have a natural ordering.

But what if the elements in our collection don’t have the Ordered trait? For example, we might want to search for the Shape with the greatest area?

Or even if the elements do have the Ordered trait, what if we want to order them by some other criterion than the natural one? For example, we might want to sort strings by length rather than alphabetically.

Often, the best thing to do is call maxBy, minBy, or sortBy.

The examples below feature Shape objects (Chapter 7.3) in addition to strings and integers. Here is a quick recap of what you need to remember about the Shape trait and its subtypes:

trait Shape:
  def area: Double
  // ...

class Circle(val radius: Double) extends Shape:
  def area = math.Pi * this.radius * this.radius
  // ...

class Rectangle(val sideLength: Double, val anotherSideLength: Double) extends Shape:
  def area = this.sideLength * this.anotherSideLength
  // ...

(We’ve also added toString methods to these classes to improve the REPL output.)

maxBy and minBy

Let’s find the longest string and the number whose second power is the greatest:

Vector("a", "bb", "b", "abc", "ba").maxBy( _.length )res5: String = abc
Vector(3, 5, -50, 20, 1, 5).maxBy( n => n * n )res6: Int = -50

The examples show the basic idea: we give maxBy a function that it calls on each element. That function’s return values must be comparable to each other, as the lengths of strings and the squares of integers are. The method determines the greatest element by comparing those return values rather than the elements themselves.

maxBy ignores any natural ordering of the elements and thus works regardless of whether such an ordering even exists. Shape objects don’t have the Ordered trait, but that doesn’t stop us from finding the shape with the greatest area:

val shapes = Vector(Circle(5), Rectangle(5, 11), Rectangle(30, 5))shapes: Vector[Shape] = Vector(CIRC[ r=5.0 a=78.54 ], RECT[ 5.0*11.0 a=55.0 ], RECT[ 30.0*5.0 a=150.0 ])
shapes.maxBy( _.area )res7: Shape = RECT[ 30.0*5.0 a=150.0 ]

minBy works the same way.

What if there are no elements? (maxByOption etc.)

Here’s one implementation for the favorite of a GoodStuff Category, which we’ve written several versions of.

def favorite = if this.experiences.isEmpty then None else Some(this.experiences.maxBy( _.rating ))

If there are no experiences, there’s no favorite, either.

Otherwise, the favorite is the experience that has the highest rating.

This code is an example of a common need: we want the biggest element or None if there aren’t any elements. Which is why there is a custom method for that task: maxByOption. This code does the same thing as the code above:

def favorite = this.experiences.maxByOption( _.rating )

There is also minByOption, as well as maxOption and minOption, which rely on a natural ordering.

Sorting with sortBy

The sortBy method is similar. You can sort strings by length, numbers by their second power, and shapes by their area:

Vector("a", "bb", "b", "abc", "ba").sortBy( _.length )res8: Vector[String] = Vector(a, b, bb, ba, abc)
Vector(3, 5, -50, 20, 1, 5).sortBy( math.pow(_, 2) )res9: Vector[Int] = Vector(1, 3, 5, 5, 20, -50)
Vector(Circle(5), Rectangle(5, 11), Rectangle(30, 5)).sortBy( _.area )res10: Vector[Double] = Vector(RECT[ 5.0*11.0 a=55.0 ], CIRC[ r=5.0 a=78.54 ], RECT[ 30.0*5.0 a=150.0 ])

With sortBy, it’s also easy to get the reverse of the natural ordering (cf. reverse above). Both of the expressions below work:

Vector(3, 5, -50, 20, 1, 5).sortBy( n => -n )res11: Vector[Int] = Vector(20, 5, 5, 3, 1, -50)
Vector(3, 5, -50, 20, 1, 5).sortBy( -_ )res12: Vector[Int] = Vector(20, 5, 5, 3, 1, -50)

In the examples just above, we used each number’s opposite rather than the number itself as the basis for sorting.

Assignment: Star Maps (Part 4 of 4: Star Catalogues; B45)

Chapter 4.4 introduced the Stars app. In Chapter 5.2, we managed to display an entire sky of stars. We’ll now develop the program further so that draws constellations.

Task description

Study class Constellation’s documentation and its incomplete code. Notice the following in particular:

  • The stars method, minCoords, and maxCoords are missing.

  • We construct a constellation from a vector of pairs.

  • The variables stars has the type Set[Star]: a set of stars.

    • A set is a collection of elements. Unlike a vector or a buffer, a set can never contain multiple copies of the same element.

    • The elements of a set don’t have numerical indices.

    • One way to form a set is to call toSet on an existing collection (e.g., myVector.toSet). Even if the original collection had multiple copies of the same elements, each element will appear only once in the resulting Set.

Add the missing parts:

  1. The program recognizes a handful of constellations, which are defined in the northern folder. You’ll need to have the right string in gui/StarryApp.scala's starDataFolder variable so that the stars (and, later, constellations) show up. Check this before you get started.

  2. Implement Constellation as specified.

  3. Implement placeConstellation in gui/skypics.scala.

  4. Edit createSkyPic in skypics.scala so that it adds the given StarMap’s constellations to the returned image (on top of the stars).

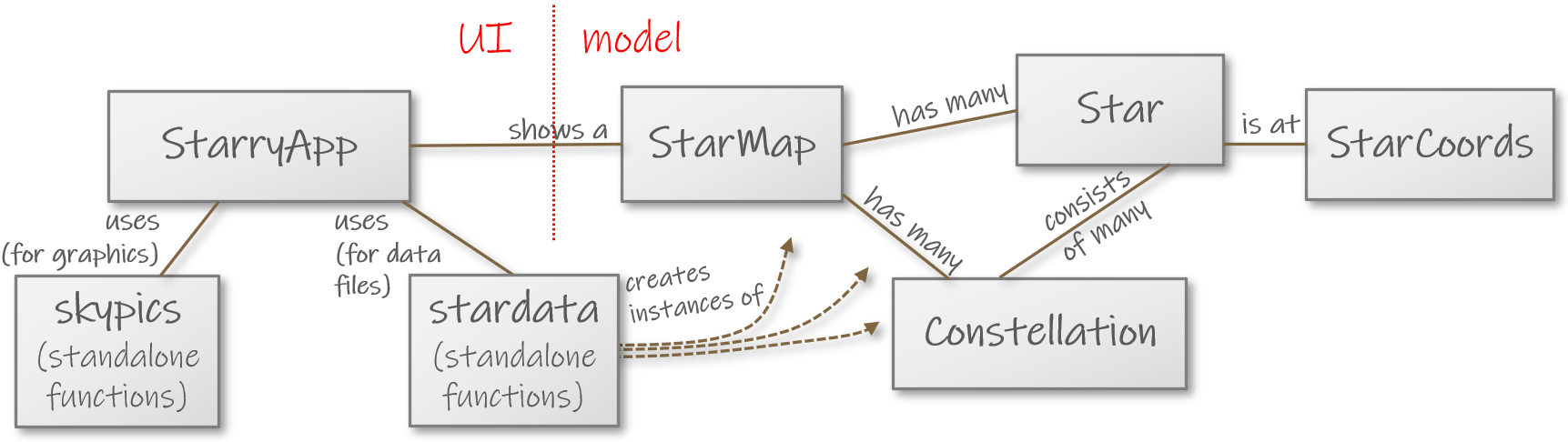
../_images/module_stars_withconstellations.png

A diagram of the Stars program.

Creating a Map from Existing Data with toMap

It’s frequently useful to create a Map from existing objects, selecting a particular property of those objects as the key.

Introduction to an example

Let’s use this Member class:

class Member(val id: Int, val name: String, val yearOfBirth: Int, val yearOfDeath: Option[Int]):
  override def toString = this.name + "(" + this.yearOfBirth + "-" + this.yearOfDeath.getOrElse("") + ")"

Now suppose we have member data in a Vector[Member]. In this example, we’ll just type in some test data in the REPL, but you can imagine the data being read from a file, for instance.

val memberVector = Vector(Member(123, "Madonna", 1958, None),
                          Member(321, "Elvis", 1935, Some(1977)),
                          Member(555, "Michelangelo", 1475, Some(1564)))memberVector: Vector[Member] = Vector(Madonna(1958-), Elvis(1935-1977), Michelangelo(1475-1564))

Given this vector, what would be an easy way to put this information in a Map that lets us look up individual members by their ID?

Preparations: pairs in a vector

The first thing we need is a way to form key–value pairs that consist of member IDs as keys and Member objects as values.

memberVector.map( member => member.id -> member )res13: Vector[(Int, Member)] = Vector((123,Madonna(1958-)), (321,Elvis(1935-1977)), (555,Michelangelo(1475-1564)))

We pass map an anonymous function that takes in a member object and...

... forms a corresponding key–value pair. We could have written brackets around this expression, just for clarity.

Making a Map from a vector

What we have now is a vector of key–value pairs. From here, it’s no trouble at all to construct a Map object. We just add a toMap call:

val memberMap = memberVector.map( member => member.id -> member ).toMapmemberMap: Map[Int,Member] = Map(123 -> Madonna(1958-),
                                 321 -> Elvis(1935-1977),
                                 555 -> Michelangelo(1475-1564))
memberMap.get(321)res14: Option[Member] = Some(Elvis(1935-1977))

toMap works nicely as long as the original collection consists of key–value pairs and each key is unique (as the IDs are, above).

toMap creates an immutable Map.

zip plus toMap

The zip method (Chapter 9.2) often comes in handy when we construct Maps. In the toy example below, we construct a Map from two existing vectors, one of which contains what will be the keys (the names of animal species) and the other of which contains the values (animal heights in centimeters).

val animals = Vector("llama", "alpaca", "vicuña")animals: Vector[String] = Vector(llama, alpaca, vicuña)
val heights = Vector(120, 90, 80)heights: Vector[Int] = Vector(120, 90, 80)

Let’s zip up these separate vectors into a vector of pairs, and we’re ready to call toMap:

val heightMap = animals.zip(heights).toMapheightMap: Map[String,Int] = Map(llama -> 120, alpaca -> 90, vicuña -> 80)
heightMap.get("alpaca")res15: Option[Int] = Some(90)

We could also have used zip in the members example, replacing this:

memberVector.map( member => member.id -> member )

with this:

memberVector.map( _.id ).zip(memberVector)

Creating a Map from Existing Data with groupBy

In the example you just saw, the keys of the Map were IDs that were unique to each Member. You can also choose to use a non-unique object property as a key. In other words, you can group objects by a particular property of theirs.

This is where the groupBy method works its magic. Just like sortBy, maxBy, and minBy, this method takes in a function that it uses to compare elements. Let’s group our members by the century they were born in:

memberVector.groupBy( _.yearOfBirth / 100 )res16: Map[Int,Vector[Member]] = Map(14 -> Vector(Michelangelo(1475-1564)),
                                     19 -> Vector(Madonna(1958-), Elvis(1935-1977)))

First, direct your attention to the Map’s type. We create a map that stores a Vector of members behind each key.

For instance, the key 19 corresponds to the 1900s. This key stores a vector with all the members who were born in that century. In this example, there are two such members.

We constructed this collection by calling groupBy and passing in a tiny function that determines a single member’s century of birth. groupBy calls this on each member in the vector. It creates and returns a Map in which...

... the keys are all the distinct values that the parameter function returns (all the different centuries) and...

... the values are collections (here: vectors, since the original collection is a vector). The original collection’s elements are divided in these collections on the basis of what the parameter function returned on each one.

partition vs. groupBy

In Chapter 9.2, we used the partition method for things such as grouping temperatures in freezing and non-freezing ones. That method was suitable for dividing elements in exactly two groups defined by a function that returns Booleans. When things aren’t that simple, you can use the more generic groupBy.

Like toMap, groupBy also generates an immutable Map object.

Assignment: Multiple Demographics (C4)

In Chapter 8.4, you implemented a city simulator with two demographics, blue and red (example solution). Let’s edit the simulator to support more groups.

../_images/schelling2.png

The updated simulator is more colorful.

Task description

Not much is required of you: just implement the residents method in class Simulator. You’ll find that it’s simple if you use groupBy in combination with the CityMap class.

The given GUI automatically detects the added method and uses it when you run the app.

A+ presents the exercise submission form here.

Example: Movie Statistics

Introduction

One fairly common use for a Map is to count occurrences.

Let’s revisit the theme of popular directors and use a Map to count how many movies each director has on a list of top-rated movies. In fact, let’s sort all the directors by this criterion. (In Chapter 1.6, you used a given function for a similar purpose.)

The following example code is also available in the MovieStats module.

This simple class Movie represents an individual entry in a top movies list:

class Movie(val name: String, val year: Int, val position: Int,
            val rating: Double, val directors: Vector[String]):
  override def toString = this.name

We also have at our disposal a class MovieListFile that is capable of reading and parsing movie data stored in text files. For present purposes, all you need to know about it is how to use it:

val movieFile = MovieListFile("omdb_movies_2015.txt")movieFile: MovieListFile = omdb_movies_2015.txt (contains: 250 movies)
val allMovies = movieFile.moviesallMovies: Vector[o1.movies.Movie] = Vector(Das Boot, Amadeus, Heat, The Secret in Their Eyes, ...

Counting occurrences with a Map

So, how to determine each director’s frequency in that long vector?

Before we count the occurrences of each director, it makes sense to list all the directors.

Since each movie can have multiple directors, just calling allMovies.map( _.directors ) doesn’t give us the single list of directors we want (but a list of movie-specific lists of directors). Let’s flatMap instead:

val allDirectors = allMovies.flatMap( _.directors )allDirectors: Vector[String] = Vector(Wolfgang Petersen, Milos Forman, Michael Mann, Juan José Campanella, ...

Let’s try to create a Map where each key is a director name and each value is the number of times that name occurs in the above vector. Here’s one way to reach that goal:

  1. Find all the occurrences of every director by grouping the vector’s elements by director name. In other words: for each name, find all its occurrences and bundle them together.

  2. Count the size of each such bundle. Put the sizes in a Map and use the director names as keys.

That sounds more complicated than it is. See below for an example.

val groupedByDirector = allDirectors.groupBy( dir => dir )groupedByDirector: Map[String,Vector[String]] = Map(Paul Thomas Anderson -> Vector(Paul Thomas Anderson),
Peter Weir -> Vector(Peter Weir), Wim Wenders -> Vector(Wim Wenders), Wolfgang Petersen -> Vector(Wolfgang Petersen),
Giuseppe Tornatore -> Vector(Giuseppe Tornatore), Robert Rossen -> Vector(Robert Rossen), Dean DeBlois ->
Vector(Dean DeBlois), Charles Chaplin -> Vector(Charles Chaplin, Charles Chaplin, Charles Chaplin, Charles Chaplin,
Charles Chaplin), Ridley Scott -> Vector(Ridley Scott, Ridley Scott, Ridley Scott), Sean Penn -> ...

Let’s see what we got: a Map where each String key (director name) stores a vector of more Strings. More specifically:

Each of the vectors contains every occurrence of the director in the original collection. Chaplin, for instance, has five movies on this list, so his name appears five times. (Most of the directors have only a single movie on the list, so their vector has but a single element.)

How we formed this Map: we called groupBy to group the director names in the big vector, using the names themselves as the grouping criterion (as odd as that may sound). See below for a discussion.

Remember: groupBy calls its parameter function on every string in the list of director names and creates a new “group” for each different value that the function returns.

So, what we do is create the groups with a function that returns exactly the same string that it takes in. This gives us a group for each different string in the original vector.

We’re close our goal now. It’s easy to create the director counts from the Map we got with groupBy; we just need a bit of help from the map method (Chapter 9.2). Let’s turn each mini-vector of identical names into the size of that vector:

val countsByDirector = groupedByDirector.map( (dir, movies) => dir -> movies.size )countsByDirector: Map[String,Int] = Map(Paul Thomas Anderson -> 1, Peter Weir -> 1, Wim Wenders -> 1,
Wolfgang Petersen -> 1, Giuseppe Tornatore -> 1, Robert Rossen -> 1, Dean DeBlois -> 1, Charles Chaplin -> 5,
Ridley Scott -> 3, Sean Penn -> 1, Danny Boyle -> 1, Gore Verbinski -> 1, Joel Coen -> 3, John Sturges -> 1, ...

Here’s a cleaner printout:

countsByDirector.foreach(println)(Paul Thomas Anderson,1)
(Peter Weir,1)
(Wim Wenders,1)
(Wolfgang Petersen,1)
(Giuseppe Tornatore,1)
(Robert Rossen,1)
(Dean DeBlois,1)
(Charles Chaplin,5)
(Ridley Scott,3)
(Sean Penn,1)
(Danny Boyle,1)
...

Sorting the directors

Let’s wrap up this example by listing the directors in order, starting with the one that has the most top-rated movies. In other words: let’s form a collection that contains all the key–value pairs of our newly created Map and sort it by the number in the pair.

We’re going to need a method that does the sorting. But first we should put the information that we have in a collection where the elements have a meaningful order. You may recall that the ordering of elements in a Map is implementation-dependent and you can’t simply sort a map. A vector, on the other hand, is good for sorting:

val directorCountPairs = countsByDirector.toVectordirectorCountPairs: Vector[(String, Int)] = Vector((Paul Thomas Anderson,1), (Peter Weir,1), (Wim Wenders,1),
(Wolfgang Petersen,1), (Giuseppe Tornatore,1), (Robert Rossen,1), (Dean DeBlois,1), (Charles Chaplin,5),
(Ridley Scott,3), (Sean Penn,1), (Danny Boyle,1), (Gore Verbinski,1), (Joel Coen,3), (John Sturges,1), ...

Now we have, in directorCountPairs, a reference to a vector that contains pairs. Now let’s sort:

val directorsSorted = directorCountPairs.sortBy( (dir, count) => -count )directorsSorted: Vector[(String, Int)] = Vector((Alfred Hitchcock,8), (Stanley Kubrick,8),
(Martin Scorsese,7), (Christopher Nolan,7), (Quentin Tarantino,6), (Steven Spielberg,6), ...

We use the opposite of the second member of each pair (the number of movies) as the sorting criterion.

The minus sign reverses the order. Without it, we’d get the least frequent directors first.

Let’s prettify that output a bit.

for (director, count) <- directorsSorted do
  println(s"$director: $count movies")Alfred Hitchcock: 8 movies
Stanley Kubrick: 8 movies
Martin Scorsese: 7 movies
Christopher Nolan: 7 movies
Quentin Tarantino: 6 movies
Steven Spielberg: 6 movies
...

That code uses Chapter 9.2’s brackets trick for iterating over pairs in a for loop.

Mini-Assignment: Maps and Sorting

Let’s assume that this code has already been executed:

val numbers = Vector(15, 7, 5, 27, 3, 8, 67, 28, 39, 15, 115, 23)
val byLastDigit = numbers.groupBy( _ % 10 )
val smallestGroupFirst = byLastDigit.toVector.sortBy( (digit, group) => group.size )

We group the numbers by their last digit.

We sort the groups based on which of the last digits is more common.

Which of the following claims about the code are correct?

Assignment: Improvements to Election (Part 1 of 2; B45)

In Chapters 5.6, 6.3, and 7.1 you worked on the Election program. However, we left several methods still unimplemented. You’ll get to implement them in this assignment and the one immediately below.

Task description

  1. Study (again) the Scaladocs in the Election module. The docs specify several methods for class District that you weren’t previously asked to implement.

  2. Rewrite topCandidate, which you already implemented once in Chapter 5.6. You should be able to come up with a much simpler implementation now.

  3. Implement the missing methods candidatesByParty, topCandidatesByParty, and votesByParty. Save the rest of the missing methods for Part 2 below.

Instructions and hints

  • If you didn’t do the earlier Election assignments, do them now or use the example solutions. If you didn’t yet write the auxiliary method countVotes, as suggested in Chapter 5.6, do that now.

  • In this assignment, you’ll be using immutable maps, which are always available in Scala without an import. Don’t import the mutable Map class from scala.collection.mutable.

  • It’s probably easiest to implement the three methods in this order: first candidatesByParty, then topCandidatesByParty, and finally votesByParty. As you implement each method, see if you can build on the methods you implemented previously.

  • Methods from this chapter will be useful. So will some other collection methods. Pick the right tools, and you won’t need to write a lot of code.

  • Test your solution with the given testElection program. There’s some useful code at the end of test.scala, which you can uncomment and run.

A+ presents the exercise submission form here.

Assignment: Improvements to Election (Part 2 of 2; C40)

Task description

Fill in the rest of the missing methods:

  1. rankingsWithinParties

  2. rankingOfParties

  3. distributionFigures

  4. electedCandidates

Instructions and hints

  • It’s probably easiest to implement the methods in the order listed above. As you implement each method, see if you can build on the methods you implemented previously.

  • Look at the examples in this and other chapters for inspiration. The movie director example may be particularly helpful.

  • Construct a vector from a map (toVector) and a map from a vector (toMap) as needed.

    • If you have trouble keeping elements sorted, revising the mini-assignment just above could help.

  • This assignment is one opportunity for defining private functions (Chapter 7.1) within a method. Try writing a def inside a def.

    • For instance, in distributionFigures, perhaps you could write an auxiliary function that determines the distribution figure of a single candidate?

A+ presents the exercise submission form here.

Summary of Key Points

  • Many programs need to compare and sort the elements of a collection.

  • Scala has a versatile API for finding maximal and minimal elements and sorting collections.

  • You can group the elements of an existing collection in a Map. One use for such groupings is to determine the distribution of similar elements.

Feedback

Please note that this section must be completed individually. Even if you worked on this chapter with a pair, each of you should submit the form separately.

Credits

Thousands of students have given feedback and so contributed to this ebook’s design. Thank you!

The ebook’s chapters, programming assignments, and weekly bulletins have been written in Finnish and translated into English by Juha Sorva.

The appendices (glossary, Scala reference, FAQ, etc.) are by Juha Sorva unless otherwise specified on the page.

The automatic assessment of the assignments has been developed by: (in alphabetical order) Riku Autio, Nikolas Drosdek, Kaisa Ek, Joonatan Honkamaa, Antti Immonen, Jaakko Kantojärvi, Onni Komulainen, Niklas Kröger, Kalle Laitinen, Teemu Lehtinen, Mikael Lenander, Ilona Ma, Jaakko Nakaza, Strasdosky Otewa, Timi Seppälä, Teemu Sirkiä, Joel Toppinen, Anna Valldeoriola Cardó, and Aleksi Vartiainen.

The illustrations at the top of each chapter, and the similar drawings elsewhere in the ebook, are the work of Christina Lassheikki.

The animations that detail the execution Scala programs have been designed by Juha Sorva and Teemu Sirkiä. Teemu Sirkiä and Riku Autio did the technical implementation, relying on Teemu’s Jsvee and Kelmu toolkits.

The other diagrams and interactive presentations in the ebook are by Juha Sorva.

The O1Library software has been developed by Aleksi Lukkarinen, Juha Sorva, and Jaakko Nakaza. Several of its key components are built upon Aleksi’s SMCL library.

The pedagogy of using O1Library for simple graphical programming (such as Pic) is inspired by the textbooks How to Design Programs by Flatt, Felleisen, Findler, and Krishnamurthi and Picturing Programs by Stephen Bloch.

The course platform A+ was originally created at Aalto’s LeTech research group as a student project. The open-source project is now shepherded by the Computer Science department’s edu-tech team and hosted by the department’s IT services; dozens of Aalto students and others have also contributed.

The A+ Courses plugin, which supports A+ and O1 in IntelliJ IDEA, is another open-source project. It has been designed and implemented by various students in collaboration with O1’s teachers.

For O1’s current teaching staff, please see Chapter 1.1.

Additional credits for this page

The Stars program is an adaptation of a programming assignment by Karen Reid. It uses star data from VizieR.

The assignment on Schelling’s model of emergent social segregation has been adapted from a programming exercise by Frank McCown.

a drop of ink
Posting submission...