Luet oppimateriaalin englanninkielistä versiota. Mainitsit kuitenkin taustakyselyssä osaavasi suomea. Siksi suosittelemme, että käytät suomenkielistä versiota, joka on testatumpi ja hieman laajempi ja muutenkin mukava.

Suomenkielinen materiaali kyllä esittelee englanninkielisetkin termit.

Kieli vaihtuu A+:n sivujen yläreunan painikkeesta. Tai tästä: Vaihda suomeksi.

Chapter 1.6: Using Subprograms

Introduction

This and next two chapters are concerned with subprograms (aliohjelma).

A subprogram is an implementation of a particular piece of functionality. For instance, a subprogram may calculate a result, record some useful data in the computer’s memory, or print out a message. Or it may perform a specific combination of such tasks.

Programmers can create new subprograms, then use what they created. They can also use subprograms created by other programmers. A full program like GoodStuff or Pong contains many subprograms.

But you’ll have to wait a bit before we can tackle how those applications work. For now, let’s proceed as follows:

In this chapter, you’ll see how to make use of custom subprograms that have been provided for you. We won’t care yet about how the subprograms that you use have been created.
Week 1’s last chapters, 1.7 and 1.8, introduce the implementations of various ready-made subprograms; that is, you’ll study how the given subprograms’ internal behavior has been defined and how those internals work as each subprogram is used. At the same time, you’ll get to practice creating subprograms of your own.

Subprograms are the last missing piece that we’ll need in Week 2 to discuss something called “object orientation”, which will help us put together entire programs.

Preparatory Steps

For this chapter, you need a new IntelliJ module called Subprograms. It contains an assortment of subprograms for you to experiment with. The instructions below recap (from Chapter 1.2) how you can download a module and use it in the REPL.

Fetch the module into IntelliJ from the A+ Courses tab at IntelliJ’s right-hand edge.
Start the REPL in the Subprograms module. Select Subprograms in the Project tab on the left. Then press Ctrl+Shift+D or pick Tools → Scala REPL in the menu.

The REPL should show up with the title REPL for Subprograms.

Example of a Custom Subprogram

Suppose we have some numbers stored in a buffer. They could be a series of scientific measurements, for example. Like so:

val results = Buffer(-2, 0, 10, -100, 50, 100, 5, -5, 2)results: Buffer[Int] = ArrayBuffer(-2, 0, 10, -100, 50, 100, 5, -5, 2)

Let’s further assume that the negative numbers in our buffer indicate failed measurements and that we wish to discard them.

It’s possible to define a subprogram that removes all negative numbers from any given buffer. Indeed, a subprogram just like that has been defined for you in the Subprograms module. It’s named removeNegatives and works like this:

When you activate the subprogram, you must provide a parameter: a reference to a buffer that contains integers.
The subprogram modifies that buffer’s contents by removing any and all negative numbers.

Calling a subprogram

Instructing the computer to execute a particular subprogram is known as calling (kutsua) the subprogram (or invoking the subprogram; or applying it).

It’s easy to call removeNegatives:

removeNegatives(results)

The command for calling the subprogram consists of the subprogram’s name and a parameter expression in round brackets.

In our example, we have only a single parameter expression. Its value is a reference to the buffer we created earlier. This reference gets passed to the subprogram for it to make use of as it carries out its task.

This command that invokes removeNegatives doesn’t itself have a value in the same sense as, say, the expression 1 + 1 does. (Well, at least the command doesn’t have a meaningful value; more on that later.) That’s why the REPL doesn’t respond with any output. However, we can take a look at the value of the results variable and verify that the subprogram did indeed modify the buffer that the variable refers to:

resultsres0: Buffer[Int] = ArrayBuffer(0, 10, 50, 100, 5, 2)

`println` and other familiar subprograms

There’s something about the preceding example that must have felt a bit familiar. The way we invoked removeNegatives there is just like how you’ve already printlned and played: first, the name of the command; then, a parenthesized parameter expression. This isn’t a coincidence.

println is a subprogram just like removeNegatives is. It’s just that println is a general-purpose subprogram defined to be a part of Scala whereas removeNegatives is an example subprogram invented for the purposes of this one ebook chapter. Similarly, play and show from Chapter 1.3 are subprograms, too.

Now let’s take a look at a rather different sort of subprogram.

A Subprogram That Returns a Value

The same module contains a subprogram named average, which has a simple purpose: you pass two numbers to it as parameters, and it computes the average of those numbers. This subprogram returns (palauttaa) a value:

average(5.0, 11.0)res2: Double = 8.0

You need to pass two numerical values to this subprogram. Separate the parameter expressions with a comma.

The invocation of average is an expression; the expression’s value is the average of two numbers, which is computed by the subprogram. This value is called the subprogram’s return value (paluuarvo). The REPL reports the value of the expression as per usual.

Here are a few more examples of calling this subprogram. As shown in the examples, you can use a subprogram-calling expression as a component of a longer expression:

val first = average(5, 1) + 2.1first: Double = 5.1
val second = average(10.9, first) + average(-5, -10) - 1second: Double = -0.5
1 + average(second + 1, 1)res1: Double = 1.75

The parameter expressions of subprogram calls don’t have to be literals. They can be variable names or any other expressions that have a compatible data type.

Program State and How to Affect It

You’ll get to see many more examples of subprograms in just a moment, but first, let’s stop to consider the attributes of the subprograms that you’ve already seen.

This chapter has introduced two very different subprograms:

Calling the removeNegatives subprogram instructs the computer to take care of a specific task. Such a call brings about changes in the state (tila) that the program has stored in the computer’s memory. We term such state-modifying subprograms effectful (vaikutuksellinen). An effectful subprogram doesn’t necessarily return any interesting value.
Calling the average subprogram doesn’t bring about any lasting changes in the data stored in memory. We term such subprograms effect-free (vaikutukseton). In order to be useful to us, an effect-free subprogram must produce a meaningful return value, as average does.

We have also used the subprogram println to output text. When a println command is executed, it has an effect on the world in the sense that the output visible onscreen changes in an observable way. This is why we’ll place println in the category of effectful subprograms along with removeNegatives. The subprograms play and show from Chapter 1.3 are similarly effectful.

That chapter also introduced circle and rectangle, which are subprograms too. These subprograms, like average, are effect-free. Just as average merely computes and returns a numerical value based on of the parameters that you give to it, circle and rectangle merely compute and return a picture based on the parameters they receive (without displaying that picture onscreen).

For any subprogram, you can ask: when you call the subprogram, does anything observably change? (We won’t count time passing or receiving a return value as a change.) The answer tells you whether the subprogram is effectful or effect-free.

Already at this early stage of O1, this classification illustrates that different subprograms can do some very different things. As we go on, you’ll see that this question has a profound significance in programming. One may even profit from programming in a way that relies exclusively on effect-free subprograms (Chapter 11.2). But let’s not get ahead of ourselves; right now, we can use the classification to illuminate a few basic terms and concepts.

An Important Term: Function

In a number of programming languages, it’s customary to call all subprograms functions (funktio), whether they are effectful or effect-free. Scala is one such language. In the rest of this ebook, the word “function” will show up often; we will use it to mean a subprogram.

The word probably sounds familiar, and there are reasons why that is so. However:

Watch out for math! (again)

Many beginner programmers have tripped over the concept of function because of the mismatch between what programmers and mathematicians mean by the word.

It’s true that effect-free functions resemble the functions from school mathematics. Given a mathematical function f(x), just determining its value for a particular x doesn’t change any stored data or output anything onscreen. Similarly, an effect-free function just takes in some parameter values and produces a result (a return value), and that’s it.

However, when you call a Scala function, it may generate output or otherwise affect program state. We must remember that our functions can be effectful!

Moreover, the functions that we use in programming, even effect-free ones, differ from familiar mathematical functions in that we don’t merely define a relation between inputs and outputs like f(x) = x + 1. Our functions also implement the step-by-step processes (algorithms) that compute the return values. The next chapter will illustrate this in detail.

Different kinds of functions, a summary

Here is a table of the kinds of functions we have just discussed. Some bits of text have been underlined; you can mouse over them to view additional explanations.

Does the function affect state?	Does it return a value?	The term we use in O1	Alternative terms
Never	Yes	Effect-free function	Function with no side effects
Never	No	Empty function	Function with no side effects
At least sometimes	Yes	Effectful function	Function with side effects, procedure
At least sometimes	No	Effectful function	Function with side effects, procedure

Library Functions from `scala.math`

The Scala language comes with a package named scala.math, which provides us with a selection of functions for common mathematical needs.

For example, the sqrt function computes and returns the square root of a given number:

scala.math.sqrt(100)res2: Double = 10.0
scala.math.sqrt(25)res3: Double = 5.0

Here, we call the function using its fully qualified name, which combines the package name scala.math and the function’s own name sqrt. (See below for how to simplify this code.)

This effect-free function does not impact on state. It only returns the result.

The same package also provides the functions max and min, which are useful in many programs. These effect-free functions return the greater and lesser of their two parameters, respectively:

scala.math.max(2, 10)res4: Int = 10
scala.math.max(15, -20)res5: Int = 15
scala.math.min(2, 10)res6: Int = 2
scala.math.min(15, -20)res7: Int = -20

In Chapter 1.1, we already touched on the concept of library (kirjasto): a selection of components that programmers can use in different projects. Scala’s mathematics package is an example of a library, and we can call functions such as the above library functions.

So. We managed to use those library functions, but it sure was unlovely that we had to write the package’s entire name in every function call. Fortunately, there is a cure for this verbosity. Let’s take a look at that before we return to more examples of functions.

Packages and the `import` Command

Code comes in packages

We’ve already mentioned a few packages of code in O1. For example:

We just used functions from the package scala.math. (This package comes with the Scala installation.)
In earlier chapters, we used tools such as play, Color, Pic from a package named o1. (In IntelliJ, you can find its code in the O1Library module.)
In Chapter 1.5, we mentioned that the Buffer type is defined in a package named scala.collection.mutable. (That package, too, comes with Scala.)

There are a number of reasons why programmers divide their tools in packages. One of the main ones is to avoid name clashes: when building a larger program as a collaborative effort, or when using tools built by others, you easily end up with the same name being used for different things in different places. In a different program, names such as play, show, or min might mean something other than what they mean in our example programs.

A solution is to place the tools with the same name in different packages. Then we can use the package names to indicate which tool we use. A downside of this approach is that whenever we need tools from a package, we are obliged to ensure that the computer knows which package we mean. Repeatedly typing in the package name is tiresome and can make the code harder to read.

Accessing packages conveniently with `import`

We can let the computer know in advance which package we intend to use later:

import scala.math.sqrt

In practice, that import command means this: “Wherever it says sqrt below, it refers to the sqrt that’s defined in package scala.math.”

The import command isn’t an expression and doesn’t have a value. The REPL doesn’t acknowledge it with any output but does receive it nonetheless.

Having so trumpeted our intention, we can now call the function simply with the word sqrt:

sqrt(100)res8: Double = 10.0
sqrt(25)res9: Double = 5.0

If we hadn’t entered the import command first, we would have received this error message:

-- Error:
  |sqrt(100)
  |^^^^
  |Not found: sqrt

If you get such an error when you program, first check that you have spelled the name correctly and that you have remembered to import.

Importing an entire package

Often we’ll want to use multiple different tools from the same package; for example, we might want to use many functions from scala.math.

We could type in a separate import command for each of the functions we need. But it’s often handier to import the package’s entire contents in one go:

import scala.math.*

You can think of that asterisk * as meaning “everything”.

Now we can use any tool in the package with no hassle:

sqrt(100)res10: Double = 10.0
max(2, 10)res11: Int = 10
min(2, 10)res12: Int = 2

Student question: Do I waste memory if I import with an asterisk?

No. An import statement is there to put on record what some words mean within a particular piece of code. For instance, importing scala.math.* indicates that the names min, max, sqrt etc. refer to functions in that package.

Yes, it’s true that the computer must hold the tools that you use in memory, functions included. But in terms of a program’s runtime memory usage, what matters is the tools you actually use, not the import commands that express your intention to use them.

When is `import` not needed?

We needed an import to use scala.math conveniently. Later on, we’ll be importing from other packages as well. However, we’ve somehow managed without import thus far, despite using functions such as println, play, and show and types such as Int, String, and Buffer. These functions and types have “simply worked”, even though they too reside in various packages. Why did we not need to import them?

Firstly: You don’t need to import the one package that is an inseparable part of Scala and named simply scala. This special package defines Int, Double, and String; for instance, the fully qualified name of Int is scala.Int. You can use any tools from this package in all Scala programs.

Secondly: Our REPL environment is set up so that it automatically imports some packages for you, so that you don’t need to start each REPL session by typing in a repetitive set of standard imports. More specifically, when you launch the REPL in one of O1’s course modules, the following happens:

You get to use the package o1 as if you had started the session by typing import o1.*. This is why it’s easy to use play and Pic in the REPL. In some modules, the REPL will import some additional course packages (as shown in the REPL’s initial welcome message). For instance, when you launched the REPL in the Subprograms module, the packages o1 and o1.subprograms were both auto-imported.
You get to use Buffers from package scala.collection.mutable as if you had imported them. We’ll use buffers a lot in O1’s early stages, so we wanted to save your fingers a bit.

If it happens that you do enter a superfluous import, nothing terrible will happen, so don’t worry. And if you forget a necessary import, you’ll get a not found error as shown above and can fix the problem.

Student question: Name conflicts when importing

What happens if I import two packages that have two functions with the same name, and then I then call the function without the package name? Which function does Scala pick, or does it pick neither?

If you do that, you get an error message complaining about the ambiguous name. Such naming conflicts are fairly common, especially if your program uses several libraries created by different programmers.

You can avoid many naming conflicts by not using the asterisk and importing only those parts of each package that you need.

If you really need to use two functions with the same name, you can always use the functions’ full names, with the package name and the dots at the front:

scala.math.sqrt(30)res13: Double = 5.477225575051661
my.imaginary.tools.rounding.sqrt(30)res14: Int = 5

Another option is to import one or both of the functions under a different name. Here’s how:

import scala.math.{sqrt as myRootFunc}myRootFunc(100)res15: Double = 10.0

Now some more functions.

Function Parade

This section will take you through a whole cavalcade of example functions. This should demonstrate the variety of things that functions can do, while letting you practice reading program code that invokes functions.

We’ll use some of Scala’s library functions as well as a number of example functions created for O1.

More library functions for math

The sqrt, max, and min functions from package scala.math were introduced above. The same package also provides other functions that instruct the computer to do math.

Examples of abs (absolute value), pow (power), and sin (sine) are shown below. To use them as shown, you’ll need to import them either individually or, as below, all at once.

import scala.math.*abs(-50)res16: Int = 50
pow(10, 3)res17: Double = 1000.0
sin(1)res18: Double = 0.8414709848078965

All those functions are effect-free. They only return values and don’t modify any data we’ve previously stored, or print or play or draw anything.

Try calling at least some of the functions in the REPL. You can also experiment with these: cbrt (cubic root), other trigonometric functions (cos, atan, etc.), floor (rounds down), ceil (rounds up), round (rounds to closest), hypot (hypotenuse of two given legs), and log and log10 (logarithms). For whole list of functions in the package, see Scala’s documentation.

Now please don’t go off trying to memorize all these library functions, let alone all the thousands of others out there, even though no doubt you’ll be needing some of them later on. You can check the names later from the Scala documentation or this ebook. When it happens, and it does happen, that a function is so frequently useful that you need it repeatedly, you’ll end up remembering it without trying. (All that being said, here’s a hint: you’ll find min and max repeatedly useful in the forthcoming chapters, so maybe make a mental note of that.)

Practice on example functions

A function can make use of external resources such as files or networked computers. The following example function (from package o1) finds out which movie is in a particular position in the all-time Top 250 according to the votes cast on the IMDb website.

imdbMovie(3)res19: String = The Godfather: Part II
imdbMovie(1)res20: String = The Shawshank Redemption

The example function works even if you don’t have a network connection, because it’s been designed to take its information from the folder top_movies that comes with the Subprograms module. This also means that the movie info isn’t quite up to date.

(Reminder: that only works if you’ve launched your REPL in the Subprograms module.)

Question 1

Use the function imdbMovie to identify the 150th best movie ever according to IMDb. Here, we number the movies in the everyday fashion from one upwards, so the two movies picked out above are the third and first on the list, respectively.

Enter the name of the 150th best movie here:

Question 2

The function imdbBestDirectors also uses the top-movies list. It sorts movie directors by how many of their movies appear on the list and returns a string containing a list of directors. The function expects to be given a single integer parameter that serves as the lower limit for inclusion. For instance, given the parameter value 2, the return value will include only those directors who have at least two movies in the Top 250.

Use imdbBestDirectors to discover who has the most movies on the list. Enter the name of the director here. (Actually, there’s a tie between two directors. Pick either of them.)

Question 3

Use the function imdbBestBetween to determine the best movie of the 1950s according to IMDb. The function expects two integer parameters: a starting year and an ending year. It returns the name of the highest-ranking movie within the given interval. The interval includes the two years you pass as parameters.

Enter the highest-rated movie of the nineteen-fifties here:

Question 4

For a change, let’s use strings as parameters and experiment with a function named editDistance. This function computes the Levenshtein distance between its two string parameters.

The Levenshtein distance is an integer that indicates how many single-character insertions, deletions, or substitutions it takes to turn one string into another. For example, the Levenshtein distance between the strings "beginner" and "engineer" is three, because we can’t manage with fewer operations than this:

Add a single n to "beginner" to get "benginner".
Remove the b to get "enginner".
Substitute one letter with another to get "engineer".

(Levenshtein distance has applications beyond spell checking. For instance, in computational genetics, it can be used for comparing DNA sequences. The genome of an organism can be represented as a string whose letters — such as A, G, C, and T — correspond to different constituents of DNA.)

Call the editDistance function, which too is defined in package o1. You’ll need to pass in two parameters of type String: the two strings to be compared. Use string literals enclosed in double quotation marks. Remember the comma.

Experiment with the function freely. Use different parameter values. In the field below, please report the Levenshtein distance between the strings "democrat" and "republican".

This assignment is entirely voluntary, just like all the other training/challenge assignments in gray-bordered boxes like this are. You’ll run into them here and there in upcoming chapters. A+ nominally awards you a single point for each bonus assignment completed, but that doesn’t count towards your grade; only A/B/C points do.

Question 1

Let’s make an animation.

Define some variables as follows.

val sizeOfLamp = 250
val redLamp    = circle(sizeOfLamp, Red)
val yellowLamp = circle(sizeOfLamp, Yellow)
val greenLamp  = circle(sizeOfLamp, Green)
val trafficLights = Buffer(redLamp, yellowLamp, greenLamp)

Package o1 provides an effectful function animate that displays a number of images one after another, thus turning them into an animation. The function expects two parameters:

a bufferful of pictures; and

a positive number (Double), that determines the speed of the animation. A larger number results in a faster animation.

Experiment with animate. In the field below, enter a command that animates the contents of the buffer that the variable trafficLights refers to. Use the speed 1.0. If you want, go ahead and come up with other things to animate.

(On some computers, the animation window may appear behind other windows, being hard to spot. If so, you’ll have to bring it to the fore manually.)

Question 1

The following code plays the internationally popular melody of Frère Jacques. Try it out.

val frereJacques = "f-g-a-f-f-g-a-f-a-hb->c---<a-hb->c---cdc<hba-f->cdc<hba-f-f-c-f---f-c-f---"
play(frereJacques)

Frère Jacques is commonly performed as a repeating canon using multiple voices or instruments: each instrument begins the melody at a somewhat different time so that the performances of the instruments overlap each other. You can form a string that represents such a canon by calling the effect-free function canon. The function is defined as follows.

As its first parameter, it expects a string that contains a melody.
As its second parameter, it expects a reference to a buffer that contains integers. It interprets the integers as the numbers of instruments.
As its third and last parameter, it expects an integer that represents the delay that each instrument initially “waits” after the previous instrument has started playing.
The function returns a string that represents a canon of the given melody played by the given instruments. (The resulting string is in a format compatible with play.)

Here’s a nearly finished piece of code that uses canon:

val frereJacques = "f-g-a-f-f-g-a-f-a-hb->c---<a-hb->c---cdc<hba-f->cdc<hba-f-f-c-f---f-c-f---"
val instruments = Buffer(4, 1, 74, 19)
play(???)

What should replace the three question marks so that the code plays a canon using the melody and instruments indicated by the variables, and a delay of 8?

Experiment in the REPL. In the field below, write the expression that calls canon as requested. (Please enter just the expression that goes where the question marks are, not the entire play command or the return value of the function.) Use the variables defined above.

Feel free to play around with canon.

Question 2

Let’s do one more exercise where we pass a buffer reference as a parameter.

Experiment with the function censor, also located in package o1. Call the function and pass in these two parameters:

this piece of text that needs censoring: "Oh, my goodness! What was that, for Pete's sake? Jeepers, where'd you get those!? For the love of Pete!"
a reference to a Buffer with three naughty words: "goodness", "Pete", and "Jeeper".

What does the censor function return, given this input?

Here’s one way to find out: Create a variable that refers to the buffer. Then call the censor function. As you call it, pass in the text as a literal and use the variable you just defined to refer to the buffer of naughty words.

The code in the preceding assignment should be of assistance.

Enter all the input strings exactly as written above. You may wish to copy and paste the returned string below so that you get it just right.

Question 3

Chapter 1.4 introduced a way of embedding values in a string using an s prefix and the dollar sign. Let’s take a quick look at how that technique combines with function calls.

The following three code fragments should each print out a number and its square root. Which of the three work? Take a guess and experiment in the REPL as needed.

(We’re assuming that import scala.math.* is in force.)

val number = 123.4
val root = sqrt(number)
println(s"The square root of $number is $root.")

val number = 123.4
println(s"The square root of $number is ${sqrt(number)}.")

val number = 123.4
println(s"The square root of $number is $sqrt(number).")

Which of the following is correct?

Only the first program works. You can’t follow the dollar sign with a function call.

The first and second programs work. You need curly brackets around the function-call expression.

All three work. The curly brackets aren’t mandatory here.

One more example

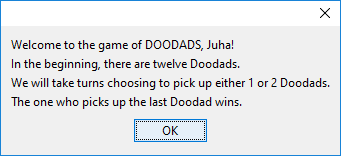
It’s perfectly possible to create a function that interacts with the user when it’s called.

Try out one such function, called playDoodads. This function challenges you to a game that lets the computer show off. It expects a single string parameter that represents the player’s name; you can use your own first name, for instance. (If your REPL seems “stuck”, with nothing else happening when you call playDoodads, it may be that the little game window has appeared behind one or more other windows. Try minimizing the IntelliJ window at least, and you should be able to find the game window.)

Nested Function Calls

When you call a function, you write expressions to indicate which parameters you wish to pass in. On the other hand, a function call is itself an expression. So it makes sense that you can nest a function call within another:

When you would end up with lots of nested function calls, you may wish to reformat your code to make it easier to read. Variables are an excellent tool for this. For instance, the last line of code in the preceding animation could be replaced by these commands:

val fifthPower = pow(2, 5)fifthPower: Double = 32.0
val smaller = min(fifthPower, 100 - sqrt(100))smaller: Double = 32.0
println(abs(-5.5) + smaller)37.5

Or these:

val fifthPower = pow(2, 5)fifthPower: Double = 32.0
val difference = 100 - sqrt(100)difference: Double = 90.0
val smaller = min(fifthPower, difference)smaller: Double = 32.0
val finalResult = abs(-5.5) + smallerfinalResult: Double = 37.5
println(finalResult)37.5

When it comes to such matters of style, use your common sense. Consider, on a case-by-case basis, what you think is best in terms of clarity and brevity. In any case, you’ll need to get used to seeing code written in all these different styles, since programmers (and learners of programming) read a lot of code written by others.

Evaluation order in nested expressions

The `Unit` value

Scala (and many other languages) feature a special value known as Unit. This value is used as the return value of functions that don’t return a value that represents meaningful information. Such functions include println and play from before and removeNegatives from this chapter. Technically, these functions also return a value, though: a Unit value.

When we receive a return value of Unit from a function, there’s practically nothing that we can do with it. You can think of it as meaning this: “The function was executed but nothing of significance was produced as a return value.” The removeNegatives function, for instance, does modify the given buffer’s state but doesn’t produce an “output” in the sense of a return value. For our practical purposes in O1, it’s okay to say that Unit means “no return value” and that functions such as println and removeNegatives “don’t return a value” or “return nothing”.

The Unit value isn’t necessarily conspicuous in the program code that you’ll write, but it isn’t just a curiosity either. If for no other reason, it’s good to be aware of Unit because you’ll see it in error messages. For instance, 1 + println("mammoth") begets a message to the effect that you “can’t add one to Unit”. Moreover, the word shows up frequently in the documentation of Scala programs to indicate that a particular program component has no significant return value.

`Unit` in O1’s animations

Unit return values haven’t appeared in the animations you’ve seen so far in this ebook. But they will be shown in future animations, such as the tiny one below.

As the animation shows, println returns a value, too, even if it’s one with no content:

Returning vs. Printing

Beginner programmers sometimes find it hard to discern just what the difference is between returning a value and printing a value. The REPL environment, useful as it is otherwise, may contribute to the confusion. So let’s take a moment to underline the difference:

Returning values is something that functions do in general. A function can communicate a value as a “response” to the party that calls the function.
- A return value doesn’t necessarily get displayed anywhere.
- It’s up to the code that calls a function to decide what it does with the return value that it receives in response; the calling code may, for instance, use the returned value as part of a calculation, or print it onscreen, or pass it as a parameter to play, or simply ignore it.
- Just returning a value from a function isn’t an “effect” on program state in the sense we’ve discussed earlier in this chapter.
By printing a value, we mean displaying text in the computer’s text console. In Scala, we accomplish this with the println command.
- The text to be printed can be determined by any expression, as in println("Hi!") and println(1 + 1).
- That expression can also be a function call, as in println(average(10, 20)). Then it’s the function’s return value that gets printed.
- Printing text onscreen is one of the things that we consider to be an effect on state.

Returning and printing in the REPL

The REPL evaluates whichever expression you type in. It then outputs a report of the value of the expression without you explicitly telling it to. If the expression specifies a function call, this means that the function gets called and a report of its return value gets reported by the REPL. So, if you enter the expression max(3 + min(1, 4), 3), you’ll see a printout that describes the return value of the max function. However, min’s return value of 1, which was used while evaluating the entire expression, does not get reported.

If you use the REPL to call a function that returns Unit, the REPL will simply discard the contentless return value.

Returning and printing within the same function

You’ve already seen that println not only prints something, it also returns a value, albeit only the Unit value. Nothing prevents programmers from defining functions that both print text onscreen and return a value.

On Functions and Abstractions

Functions as tools

Some goals are easily reached because there is a tool available for them. For instance, if our goal is to compute the sine or square root of a particular number, we can simply call a library function to do that.

If we can’t find such a ready-made solution to our exact problem, we’ll form our own by combining the tools that are available to us. If, for instance, we wish to find out the volume of a sphere whose radius is 6371 km, we can use arithmetic operators and the exponentiation function pow:

import scala.math.pow4 * 3.14159 * pow(6371, 3) / 3res21: Double = 1.0832060019000126E12

Above, we evaluated a specific expression that contains specific numbers that gave us a specific result. But if we want to handle a variety of different cases — compute the volumes of various spheres of various sizes — it’s more practical to build a custom tool for that purpose. Perhaps our tool could work like this:

volumeOfSphere(6371)res22: Double = 1.0832060019000126E12
volumeOfSphere(1)res23: Double = 4.188786666666666

Benefits of custom functions

You just saw one reason why we might wish to create our own custom functions: when we have implemented a function that solves a particular, perhaps complex task, we can easily reuse the solution by calling the function. Moreover, writing functions helps programmers avoid reinventing the sphere: a function, once written, can be distributed for other programmers to use.

Functions also have a role in organizing program code into named components that are clearly delimited. This makes the code easier to understand and modify.

One more benefit arises from how a function hides within itself the implementation of a particular solution, whose details are unnecessary for the function’s user to know. As long as a programmer has access to a volumeOfSphere function, they can use it even without knowing the formula for calculating volumes. In this chapter, you yourself have called various functions even though you couldn’t have implemented the functions yourself, or even understood their implementation, given just what we’ve covered so far. It’s been enough that you’re familiar with a few aspects of each function: what kinds of parameters it expects, what effects (if any) it brings about, and what it returns.

In other words, functions are a form of abstraction (abstraktio) in programming.

Abstractions in programming

abstract: something that concentrates in itself the essential qualities

of anything more extensive or more general; essence

—a definition of “abstract” at Infoplease.com

By abstracting, we can choose to ignore details and specific cases. For instance, the function volumeOfSphere represents the general, abstract algorithm for computing the volume of any sphere.

Besides functions, you’ve already encountered other programming abstractions as well. A variable is an abstraction: in the expression number + 1, the name of the variable is there to indicate that we wish to sum two values without concerning ourselves (at that juncture) with what specific value might be stored in the variable number.

Function parameters promote abstraction. Consider the function sin, which takes a parameter (as in sin(1)). That function’s programmer didn’t cater to just one use case of the function but to any and all possible parameter values. Consequently, the function is more abstract and more generally useful than a variable sineOfOne.

Programming revolves around the design, implementation, and use of abstractions. This is a theme that we’ll return to repeatedly (in Chapters 2.1 and 3.2, among others). Creating your own custom functions is something you’ll get to practice right away in the next chapter.

Summary of Key Points

A subprogram is an implementation of a specific piece of functionality. In many contexts, including O1, subprograms are known as functions.
A function can have an effect on program state or return a value (such as the result of a computation) or both.
Telling the computer to execute a function is known as calling or invoking the function. As you call a function, you may pass parameters to it.
Programming languages come with libraries that contain functions and other program components. Scala’s library contains a number of mathematical functions, among many other things.
Functions are one of several forms of abstraction in programming. Abstractions enable people to work on complex wholes and help eliminate repetitive labor.
Unit is a special value that means, roughly, “no meaningful (return) value”.
The import command comes in handy when you want to use the tools contained in a particular package.
- Our REPL environment does the most obvious imports automatically for you, but even in the REPL, you’ll sometimes need to import packages such as scala.math.
Links to the glossary: function / subprogram; function call, parameter expression, return value; effect-free function, effectful function; Unit; library; abstraction.

Here’s the concept map from the previous chapter, newly adorned with functions:

Credits

Thousands of students have given feedback and so contributed to this ebook’s design. Thank you!

The ebook’s chapters, programming assignments, and weekly bulletins have been written in Finnish and translated into English by Juha Sorva.

The appendices (glossary, Scala reference, FAQ, etc.) are by Juha Sorva unless otherwise specified on the page.

The automatic assessment of the assignments has been developed by: (in alphabetical order) Riku Autio, Nikolas Drosdek, Kaisa Ek, Joonatan Honkamaa, Antti Immonen, Jaakko Kantojärvi, Onni Komulainen, Niklas Kröger, Kalle Laitinen, Teemu Lehtinen, Mikael Lenander, Ilona Ma, Jaakko Nakaza, Strasdosky Otewa, Timi Seppälä, Teemu Sirkiä, Joel Toppinen, Anna Valldeoriola Cardó, and Aleksi Vartiainen.

The illustrations at the top of each chapter, and the similar drawings elsewhere in the ebook, are the work of Christina Lassheikki.

The animations that detail the execution Scala programs have been designed by Juha Sorva and Teemu Sirkiä. Teemu Sirkiä and Riku Autio did the technical implementation, relying on Teemu’s Jsvee and Kelmu toolkits.

The other diagrams and interactive presentations in the ebook are by Juha Sorva.

The O1Library software has been developed by Aleksi Lukkarinen, Juha Sorva, and Jaakko Nakaza. Several of its key components are built upon Aleksi’s SMCL library.

The pedagogy of using O1Library for simple graphical programming (such as Pic) is inspired by the textbooks How to Design Programs by Flatt, Felleisen, Findler, and Krishnamurthi and Picturing Programs by Stephen Bloch.

The course platform A+ was originally created at Aalto’s LeTech research group as a student project. The open-source project is now shepherded by the Computer Science department’s edu-tech team and hosted by the department’s IT services; dozens of Aalto students and others have also contributed.

The A+ Courses plugin, which supports A+ and O1 in IntelliJ IDEA, is another open-source project. It has been designed and implemented by various students in collaboration with O1’s teachers.

For O1’s current teaching staff, please see Chapter 1.1.

Additional credits for this page

This chapter does injustice to music by Neal Hefti, Mike Oldfield, and Dave Stewart. Thank you and sorry.

Thanks to Alex Purovesi for suggesting an improvement to the Doodads game.

Chapter 1.6: Using Subprograms

Introduction

Preparatory Steps

Example of a Custom Subprogram

Calling a subprogram

println and other familiar subprograms

A Subprogram That Returns a Value

Program State and How to Affect It

An Important Term: Function

Watch out for math! (again)

Different kinds of functions, a summary

Library Functions from scala.math

Packages and the import Command

Code comes in packages

Accessing packages conveniently with import

Importing an entire package

When is import not needed?

Function Parade

More library functions for math

Practice on example functions

One more example

Nested Function Calls

Evaluation order in nested expressions

The Unit value

Unit in O1’s animations

Returning vs. Printing

Returning and printing in the REPL

Returning and printing within the same function

On Functions and Abstractions

Functions as tools

Benefits of custom functions

Abstractions in programming

Summary of Key Points

Feedback

Credits

Additional credits for this page

`println` and other familiar subprograms

Library Functions from `scala.math`

Packages and the `import` Command

Accessing packages conveniently with `import`

When is `import` not needed?

The `Unit` value

`Unit` in O1’s animations