1. CS-A1110
  2. Kierros 6
  3. Luku 6.3: Kokoelmia ja madonruokaa

Luku 6.3: Kokoelmia ja madonruokaa

../_images/person09.png

Johdanto

Tämä luku esittelee valikoiman metodeita, joita voi käyttää silmukoiden sijaan tai lisäksi kokoelmia käsitellessä. Metodeille on yhteistä se, että ne löytyvät Scalan valmiilta kokoelmatyypeiltä sekä se, että ne vastaanottavat parametreina funktioita, jotka täsmentävät sitä, mitä kokoelman alkioilla tehdään. Metodit vastaavat muun muassa näihin tarpeisiin:

  • Miten toistan tietyn toimenpiteen kullekin alkiolle kokoelmassa (esim. tulostan kunkin alkion)?

  • Miten tutkin kokoelman yleisiä ominaisuuksia (esim. ovatko kaikki alkiot tietynlaisia)?

  • Miten valikoin alkioita kokoelmasta (esim. kaikki alkiot, jotka ovat tietynlaisia)?

  • Miten muodostan tuloksen yhdistelemällä kokoelman alkioita (esim. lukujen neliöiden summa tai kuvia päällekkäin sijoittamalla saatu yhdistelmä)?

  • Miten muodostan toisen alkiokokoelma, jonka kukin alkio saadaan tietyllä "kaavalla" alkuperäisestä kokoelmasta (esim. henkilöolioiden luettelosta henkilötunnusten luettelo)?

Näiden korkeamman asteen metodien käyttö on usein kätevää; niitä käyttäen kirjoitettu koodi on usein lyhyttä ja selkeää. Esitellyt metodit ovat erityisen ominaisia funktionaaliselle ohjelmointityylille (mistä lisää luvussa 11.2), kun taas imperatiivisessa ohjelmointitavassa silmukat ovat perinteisesti yleisempiä.

Osa luvusta koostuu pienistä irrallisista esimerkeistä, jotka esittelevät almiiden metodien käyttöä. Tämä luku on eräänlainen jatko-osa luvulle 4.1, jossa esiteltiin eräitä kokoelmien ensimmäisen asteen metodeita.

Monissa seuraavista esimerkeistä käytetään selkeyden vuoksi kokonaislukuvektoreita. Silti aivan samat metodit toimivat myös muille alkiotyypeille kuin luvuille ja muunlaisille Scala-peruskirjastojen kokoelmille kuin vektoreille.

Esimerkeissä esiintyy paljon funktioliteraaleja — sekä tavallisia että alaviivoin lyhennettyjä — joten varmista, että olet ymmärtänyt edellisen luvun esittelemät merkintätavat.

Toimenpiteen toistaminen alkioille: foreach

Scala-kokoelmille määritellyistä korkeamman asteen metodeista tavallaan yleiskäyttöisin on nimeltään foreach. Koekäytetään sitä vektorin sisältämien lukujen neliöiden tulostamiseen.

val luvut = Vector(10, 5, 4, 5, -20)luvut: Vector[Int] = Vector(10, 5, 4, 5, -20)
luvut.foreach( n => println(n * n) )100
25
16
25
400

foreach-metodille annetaan parametriksi funktio, jolle kelpaa parametriksi kokoelman alkioiden tyyppinen arvo (tässä Int). Esimerkiksi tässä määritelty funktioliteraali siis on sopiva.

foreach nimensä mukaisesti suorittaa parametriksi annetun funktion kertaalleen kullekin kokoelman sisältämälle alkiolle. Tässä tapauksessa kustakin alkiosta lasketaan toinen potenssi ja tulostetaan se.

Vaikka metodin nimi tulee kahdesta englannin kielen sanasta — for each — niin siinä ei poikkeuksellisesti ole isoa E-kirjainta.

Lienet jo huomannut, että foreach on toiminnaltaan samankaltainen kuin luvussa 6.1 laatimasi repeatForEachElement-funktio. foreach eroaa tuosta aiemmasta funktiosta ennen muuta olemalla kokoelmaolioille valmiiksi määritelty metodi, jota voit käyttää missä vain Scala-ohjelmassa.

Koska foreach-metodille annetaan parametriksi arvoa palauttamaton funktio, niin sitä käytetään parametrifunktion aiheuttamien vaikutuksien vuoksi. Jotta metodikutsu olisi hyödyllinen, on parametrifunktion esimerkiksi tulostettava jotain (kuten yllä) tai vaikutettava jonkin olion tilaan.

Silmukat vs. kokoelmien metodit

Kuten yllä mainittiin, tässä luvussa käsiteltävillä metodeilla voi tehdä samanlaisia asioita kuin silmukoilla. Tämä korostuu erityisesti ensimmäisessä esimerkissämme eli foreach-metodissa. Voidaanhan kirjoittaa myös:

for n <- luvut do
  println(n * n)

Tosiaan, nämä kaksi tekevät keskenään ihan saman:

for alkio <- alkioita do
  Tee jotain alkiolla.
alkioita.foreach( alkio => Tee jotain alkiolla. )

Itse asiassa tällainen for-silmukka on vain erilainen tapa merkitä foreach-metodikutsu; Scala-kääntäjä tulkitsee sen metodikutsuksi.

Tässä vielä esimerkki AuctionHouse-luokan metodista, joka toteutettiin siellä näin:

def nextDay() =
  for current <- this.items do
    current.advanceOneDay()

Olisimme voineet kirjoittaa näinkin:

def nextDay() =
  this.items.foreach( item => item.advanceOneDay() )

Riippuu tilanteesta ja mieltymyksistä, kumpi tapa on luontevampi ja selkeämpi.

Kurssin tulevissa esimerkeissä käytetään foreach-metodia varsin usein (mutta for-silmukkaa myös). Voit itse käyttää kumpaa haluat, mutta sivistyneen Scala-ohjelmoijan on syytä tuntea molemmat tavat.

A+ esittää tässä kohdassa tehtävän palautuslomakkeen.

Tehtävä: Election-ratkaisua uusiksi (osa 1/3)

Luvussa 5.6 toteutit metodeita Election-moduulin District-luokkaan. (Jos et toteuttanut, tee se nyt tai ota esiin sen tehtävän esimerkkiratkaisu.) Silloin käytit silmukoita.

Toteuta metodeista nyt yksi uusiksi: printCandidates. Käytä silmukan sijaan foreach-metodia.

Palaamme District-luokan muihin metodeihin vielä.

A+ esittää tässä kohdassa tehtävän palautuslomakkeen.

Välipuhe abstraktiotasoista

Nimettömien parametrien rajoituksia (osa 1/2)

Edellinen luku 6.2 näytti, että funktioliteraaleja voi Scalassa kirjoittaa joko täydessä muodossaan nuolta => käyttäen tai lyhyemmin alaviivaa _ käyttäen. Jälkimmäisessä tapauksessa nimettömiksi jäävät paitsi funktio itse, myös sen parametrit.

Esimerkiksi nämä tekevät keskenään saman asian:

(eka, toka) => eka + toka + 10

_ + _ + 10

Lyhyempää merkintätapaa voi käyttää usein muttei aina. Ennen kuin jatketaan uusien kokoelmametodien parissa, tarkastellaan paria esimerkkiä, jotka näyttävät, millaisissa tilanteissa lyhennetty muoto ei toimi.

Seuraava funktio laskee tuloksen parametrinsa perusteella. Sen rungossa sama parametri­muuttuja esiintyy useammin kuin kerran.

def laske(luku: Double) = luku * luku + 10

Saman toiminnallisuuden voi kirjoittaa nimettömänä funktiona näin:

luku => luku * luku + 10

Sen sijaan tämä lyhennetty versio ei toimi halutusti:

_ * _ + 10

Koska kukin alaviiva vastaa erillistä nimetöntä parametria, äskeinen lyhennetty literaali ajaa saman asian kuin nämä pidemmät versiot:

(luku1, luku2) => luku1 * luku2 + 10

def laske(luku1: Double, luku2: Double) = luku1 * luku2 + 10

Kyseessä on siis aivan toinen, kaksiparametrinen funktio.

Kuhunkin nimettömään parametriin voi viitata vain yhdestä kohdasta funktioliteraalia; kukin alaviiva viittaa eri parametriin, järjestyksessä. Jos haluat viitata johonkin funktioliteraalin parametreista useasti, käytä lyhentämätöntä funktioliteraalia nimetyillä parametreilla.

Toinen esimerkki samasta rajoituksesta:

luvut.foreach( luku => println(luku * luku) )

Parametrimuuttuja luku esiintyy rungossa useasti, joten parametri on tarpeen nimetä.

Tässä uusintana yllä käsitelty foreach-metodikutsu:

this.items.foreach( item => item.advanceOneDay() )

Voiko tuon funktioliteraalin kirjoittaa toisin käyttäen nimellisen item-parametrin sijaan alaviivalle merkittyä nimetöntä parametria?

Edellisessä luvussa 6.2 käsiteltiin tätä funktiota:

def swapGreenAndBlue(original: Color) =
  Color(original.red, original.blue, original.green)

Funktiota voi käyttää esimerkiksi näin:

myPic.transformColors(swapGreenAndBlue)

Totesimme, että erillisen nimetyn funktion sijaan voisi käyttää funktioliteraalia:

myPic.transformColors( orig => Color(orig.red, orig.blue, orig.green) )

Voiko tuon literaalin kirjoittaa uusiksi alaviivalla eli Color(_.red, _.blue, _.green)?

Tarkoitus on täydentää tämä korkeamman asteen metodikutsu, joka luo 200 kertaa 200 -kokoisen kuvan:

Pic.generate(200, 200, ??? )

Tässä on eräs funktioliteraali, joka sopii kysymysmerkkien paikalle:

(x, y) => Color(x, y, 0)
../_images/xy0.png

(Tuolla käskyllä saadaan aikaan oheinen kuva, jossa punaisuus kasvaa oikealle, vihreys alaspäin ja sinisyys on nollassa.)

Voiko tuon literaalin kirjoittaa uusiksi muotoon Color(_, _, 0)?

../_images/y0x.png

Tässä toinen kuvan tuottava metodikutsu:

Pic.generate(200, 200, (x, y) => Color(y, 0, x) )

Voiko tuon literaalin kirjoittaa uusiksi muotoon Color(_, 0, _)?

Vielä yksi esimerkki:

myPic.transformColors( pixel => pixel.lighter )

Voiko tuon funktioliteraalin kirjoittaa uusiksi käyttäen nimellisen parametrin paikalla alaviivalla merkittyä nimetöntä parametria?

Kokoelman ominaisuuksien tutkiminen

Tutustutaan muutamaan muuhunkin kokoelmien metodiin.

exists- ja forall-metodit

exists-metodilla voi kätevästi selvittää, toteutuuko tietty kriteeri minkään alkion osalta:

val luvut = Vector(10, 5, 4, 5, -20)luvut: Vector[Int] = Vector(10, 5, 4, 5, -20)
luvut.exists( _ < 0 )res0: Boolean = true
luvut.exists( _ < -100 )res1: Boolean = false

exists-metodille annetaan parametriksi funktio, joka ottaa parametrikseen kokoelman alkion ja palauttaa totuusarvon, joka kertoo, toteuttaako kyseinen alkio kriteerin. Esimerkiksi tässä välitetään ensin parametriksi funktio, joka kertoo, onko sen parametriarvo negatiivinen.

Esimerkkikokoelmastamme löytyy (ainakin yksi) alkio, joka on negatiivinen. Sieltä ei löydy yhtään alkiota, joka olisi miinus sataa pienempi.

forall-metodi vastaavasti tutkii, päteekö annettu kriteeri kaikille alkioille:

luvut.forall( _ > 0 )res2: Boolean = false
luvut.forall( _ > -100 )res3: Boolean = true

Tässä tutkittiin ensin, ovatko kaikki alkiot positiivisia; eivät ole. Toisella forall-kutsulla selvisi, että kaikki alkiot ovat miinus satasta suurempia.

Pikkutehtäviä: exists, forall ja count

A+ esittää tässä kohdassa tehtävän palautuslomakkeen.

Päättele esimerkiksi REPLissä kokeilemalla, mitä kokoelmien count-metodi tekee. Kokeile käskyä luvut.count( _ % 2 == 0 ) ja muita vastaavia.

Mikä tai mitkä seuraavista pitävät paikkansa, kun jokuEhto on funktion nimi ja kokoelma on johonkin alkiokokoelmaan viittaava muuttuja? Oletetaan, että jokuEhto-funktio on tyypiltään kyseiselle kokoelmalle sopiva. (Esimerkiksi jos kokoelman alkiot ovat Int-tyyppisiä, jokuEhto ottaa parametriksi yhden Intin. Se palauttaa joka tapauksessa Boolean-arvon.)

Alla kysytään, mitkä väitteistä pitävät aina paikkansa kokoelman koosta riippumatta. Muista, että kokoelma voi sisältää alkioita tai se voi olla tyhjä!

Jos luot tyhjän kokoelman kokeiluja varten, muista kirjoittaa tyyppiparametri. Siis esim. Vector[String]() tai Buffer[Int]() eikä vain Vector() tai Buffer().

Operaattorit tuollaisissa funktioliteraaleissa

Äskeisen tehtävän funktioliteraaleissa esiintyi negaatio-operaattori !. Esimerkiksi tämä on mahdollinen Scala-käsky:

kokoelma.forall( alkio => !jokuEhto(alkio) )

Voisiko tuon kirjoittaa toisinkin? Arvioi seuraavien vaihtoehtojen toimivuutta.

Alkioiden valikoiminen kokoelmasta

find-, filter-, takeWhile- ja dropWhile-metodit

find-metodi etsii ensimmäisen alkion, joka täyttää parametrifunktion määrittelemän kriteerin. Esimerkiksi tässä etsitään ensimmäinen viitosta pienempi luku:

val luvut = Vector(10, 5, 4, 5, -20)luvut: Vector[Int] = Vector(10, 5, 4, 5, -20)
luvut.find( _ < 5 )res4: Option[Int] = Some(4)

Huomaa: find palauttaa Option-arvon, johon on "kääritty" löydetty alkio. Jos haku oli "huti", saadaan None:

luvut.find( _ == 100 )res5: Option[Int] = None

filter-metodi on samansuuntainen kuin find, mutta se palauttaa kokoelman kaikista niistä alkioista, jotka täyttävät kriteerin. Esimerkiksi tässä vektorista löytyy neljä positiivista lukua:

val luvut = Vector(10, 5, 4, 5, -20)luvut: Vector[Int] = Vector(10, 5, 4, 5, -20)
luvut.filter( _ > 0 )res6: Vector[Int] = Vector(10, 5, 4, 5)

Luvussa 4.1 esiteltiin kokoelmien take-metodi, joka palauttaa osakokoelman, jossa on parametriksi annettu lukumäärä alkioita alkuperäisen kokoelman alusta (esim. luvut.take(3)). Tämän metodin korkeamman asteen serkku on takeWhile:

val luvut = Vector(10, 5, 4, 5, -20)luvut: Vector[Int] = Vector(10, 5, 4, 5, -20)
luvut.takeWhile( _ >= 5 )res7: Vector[Int] = Vector(10, 5)

Metodi siis poimi kokoelman alusta peräkkäisiä alkioita kunnes kohdataan sellainen, joka ei täytä parametrin määräämää kriteeriä.

A+ esittää tässä kohdassa tehtävän palautuslomakkeen.

Pikkutehtäviä: filter vs. filterNot, takeWhile vs. dropWhile

Päättele esimerkiksi REPLissä kokeilemalla, mitä kokoelmien filterNot-metodi tekee. Sitä kutsutaan samaan tapaan kuin filter-metodia yllä.

Oletetaan, että on määritelty vektoriin viittaava muuttuja nimeltä kokoelma sekä tehty def-määrittely, joka luo tyypiltään sopivan jokuEhto-nimisen funktion. Mikä tai mitkä seuraavista pitävät paikkansa?

Entä mitä tekee dropWhile-metodi? Sitä kutsutaan samaan tapaan kuin takeWhile-metodia aiemmissa esimerkeissä.

Tehtävä: Election-ratkaisua uusiksi (osa 2/3)

[Tämä] tehtävä oli kyllä hyvä,
lyhenipä koodi kummasti.

Toteuta District-luokasta toinenkin metodi uusiksi: candidatesFrom. Sille on olemassa yksinkertainen toteutus, jos käytät for-silmukan sijaan yhtä yllä esitellyistä metodeista.

A+ esittää tässä kohdassa tehtävän palautuslomakkeen.

Nimettömien parametrien rajoituksia (osa 2/2)

Katsotaan tässä välissä toinen funktioliteraalien käyttöön vaikuttava seikka. Se selviää parhaiten esimerkkien avulla. Esimerkeissä käytämme näitä edeltä tuttuja funktioita kahdesti ja tuplaa:

def kahdesti(toiminto: Int => Int, kohde: Int) =
  toiminto(toiminto(kohde))

def tuplaa(tuplattava: Int) = 2 * tuplattava

Jos tavoitteena on soveltaa tuplaa-funktiota kahdesti lukuun 1000, kaikki nämä koodinpätkät toimivat:

kahdesti(tuplaa, 1000)              // pelkkä funktion nimi riittää

kahdesti( x => tuplaa(x) , 1000)    // tavallinen funktioliteraali

kahdesti( tuplaa(_) , 1000)         // lyhennetty funktioliteraali

Seuraavassa esimerkissä tehdään kahdesti seuraava: ensin tuplaa luku ja lisää sitten ykkönen. Esimerkiksi luvusta 1000 tulisi ((1000*2+1) * 2 + 1 eli 4003. Kumpi vain seuraavista toimii:

kahdesti( x => tuplaa(x) + 1 , 1000)    // tavallinen funktioliteraali

kahdesti( tuplaa(_) + 1 , 1000)         // lyhennetty funktioliteraali

Entäpä seuraava esimerkki? Nyt haluttaisiin toistaa kahdesti tätä: lisää ensin ykkönen ja tuplaa sitten. Esimerkiksi luvusta 1000 tulisi ((1000+1)*2 + 1) * 2 eli 4006. Tämä funktioliteraali hoitaa homman:

kahdesti( x => tuplaa(x + 1) , 1000)     // tavallinen funktioliteraali

Voisi hyvin ajatella, että tuo sopii lyhentää näin:

kahdesti( x => tuplaa(_ + 1) , 1000)  // ei toimi!

Tämä ei kuitenkaan toimi. Keskeinen seikka on, että alkuperäisessä funktioliteraalissa on sulkeet, joiden sisällä parametri x ei ole yksinään vaan osana lauseketta x + 1.

Tällaisessa tapauksessa alaviiva "lavennetaan vain sisimpien sulkeiden sisällä", ja funktioliteraaliksi ei tulkita koko koodinpätkää vaan vain sulkeiden sisäinen osa koodinpätkästä. Siksi literaali tuplaa(_ + 1) tarkoittaa tuplaa(x => x + 1), joka ei ole kelvollista koodia, koska tuplaa-funktiolle ei voi antaa parametriksi funktiota.

Tuo lyhennetty versio ei siis tarkoita sitä, mitä haluttiin. Tuollainen koodi onneksi kuitenkin tuottaa välittömän käännösaikaisen virheen eikä ajonaikaista bugia.

Kun tarvitset funktioliteraalin parametria sulkeiden sisällä johonkin laskutoimitukseen, älä lyhennä alaviivalla vaan anna parametrille nimi. Jos tämä sääntö tuntuu epäselvältä, voit mainiosti kirjoittaa aina kaikki literaalit pitkinä.

Oletetaan, että on olemassa lukuja sisältävä vektori ja siihen viittaava muuttuja, vaikkapa näin:

val luvut = Vector(56.0, 120.0, 0.0, 36.5, 1234.5, 10000.0)

Oletetaan lisäksi, että neliöjuuren laskeva sqrt-funktio on importattu näin:

import scala.math.sqrt

Seuraava filter-kutsu poimii luvuista kaikki ne, jotka täyttävät funktioliteraalin määräämän kriteerin:

luvut.filter( luku => sqrt(luku + 20) < 40 )

Voiko tuon literaalin lyhentää näin?

luvut.filter( sqrt(_ + 20) < 40 )

Tässä toinen filter-kutsu:

luvut.filter( luku => sqrt(luku) + 20 < 40 )

Voiko tuon literaalin lyhentää näin?

luvut.filter( sqrt(_) + 20 < 40 )

Entäpä tämä...

luvut.filter( luku => luku + sqrt(20) < 40 )

... voiko sen lyhentää näin?

luvut.filter( _ + sqrt(20) < 40 )

Ja vielä yksi. Arvioi seuraavaa foreach-metodikutsua. Oletetaan, että lajit on tyypiltään Vector[String].

lajit.foreach( laji => println(laji + " on eläin") )

Voiko tuon literaalin lyhentää näin?

lajit.foreach( println(_ + " on eläin") )

Alkioiden kuvaaminen toisiksi: map- ja flatMap-metodit

Tutkitaan vielä kahta kokoelmien metodia.

Eräs erittäin usein hyödyllinen toimenpide on alkiokokoelman kuvaaminen eli "mäppäys" toiseksi alkiokokoelmaksi.

map-metodi palauttaa uuden kokoelman, jonka kukin alkio on saatu soveltamalla parametrifunktiota alkuperäisen kokoelman alkioon. Ensimmäisessä esimerkissämme map-käsky laskee kustakin vektorin alkiosta itseisarvon ja palauttaa uuden vektorin, jossa itseisarvot ovat alkuperäisiä alkioita vastaavassa järjestyksessä:

val luvut = Vector(10, 5, 4, 5, -20)luvut: Vector[Int] = Vector(10, 5, 4, 5, -20)
luvut.map( _.abs )res8: Vector[Int] = Vector(10, 5, 4, 5, 20)

Seuraava map-käsky puolestaan selvittää kustakin alkiosta, onko se vähintään viisi. Tulosvektorissa ovat järjestyksessä näin saadut totuusarvot:

luvut.map( _ >= 5 )res9: Vector[Boolean] = Vector(true, true, false, true, false)

map-metodilla voi kohdistaa mitä moninaisimpia muutosfunktioita useaan alkioon kerralla. Kuten muutkin tämän luvun esittelemät metodit, se löytyy myös muilta alkiokokoelmilta kuin vektoreilta. Esimerkiksi 1 to 10 -lausekkeen arvoksi syntyvä Range-olio (luku 5.6) on kokoelma:

(1 to 10).map( n => n * n )res10: IndexedSeq[Int] = Vector(1, 4, 9, 16, 25, 36, 49, 64, 81, 100)

Tässä vielä yksi esimerkki, jossa alkioina on Double-arvoja ja käytämme nimettyä funktiota:

import scala.math.sqrtval data = Vector(100.0, 25.0, 12.3, 2, 1.21)data: Vector[Double] = Vector(100.0, 25.0, 12.3, 2.0, 1.21)
data.map(sqrt)res11: Vector[Double] = Vector(10.0, 5.0, 3.5071355833500366, 1.4142135623730951, 1.1)

Neliöjuurifunktion soveltaminen kuhunkin alkioon tuottaa kokoelman, jossa on alkuperäisten lukujen neliöjuuret.

Pieniä map-tehtäviä

A+ esittää tässä kohdassa tehtävän palautuslomakkeen.

Tavoitteena on tulostaa riveittäin raportit vektorin sisältämien lukujen neliöistä. Alla on foreach-kutsu ja map-kutsu. Vertaa niitä:

val lukuja = Vector(10, -5, 20)lukuja: Vector[Int] = Vector(10, -5, 20)
lukuja.foreach( luku => println("Neliö on " + luku * luku) )Neliö on 100
Neliö on 25
Neliö on 400
lukuja.map( luku => println("Neliö on " + luku * luku) )Neliö on 100
Neliö on 25
Neliö on 400
res12: Vector[Unit] = Vector((), (), ())

Päättele tai arvaa, mitkä seuraavista tuota esimerkkiä koskevista väitteistä pitävät paikkansa. Lue saamasi palaute.

Tavoitteena on saada vektori, jossa on alkuperäisen vektorin sisältämien lukujen neliöt. Alla on foreach-kutsu ja map-kutsu. Vertaa niitä:

lukuja.foreach( luku => luku * luku )lukuja.map( luku => luku * luku )res13: Vector[Int] = Vector(100, 25, 400)

Arvioi tuota koodia koskevat väitteet.

Oletetaan, että muuttuja puskuri on alustettu osoittamaan Buffer[Int]-tyyppiseen kokoelmaan eli kokonaislukuja sisältävään "yksiulotteiseen" puskuriin. Oletetaan myös, että tuossa puskurissa on ainakin yksi alkio.

Mitä tapahtuu, kun evaluoidaan puskuri.map( x => Buffer(x, x + 1) )? Tutki itse REPLissä tarpeen mukaan.

flatMap-metodi

Luvussa 6.1 näyttäytyi metodi flatten, joka "litistää" kokoelmia sisältävän kokoelman:

val sisakkain = Vector(Vector(3, -10, -4), Vector(5, -10, 1), Vector(-1), Vector(4, 4))sisakkain: Vector[Vector[Int]] = Vector(Vector(3, -10, -4), Vector(5, -10, 1), Vector(-1), Vector(4, 4))
sisakkain.flattenres14: Vector[Int] = Vector(3, -10, -4, 5, -10, 1, -1, 4, 4)

On melko yleistä, että halutaan suorittaa peräkkäin map ja flatten: ensin "mäppäys" ja sitten litistäminen. Tässä pieni kokeiluesimerkki:

val luvut = Vector(10, 5, 4, 5, -20)luvut: Vector[Int] = Vector(10, 5, 4, 5, -20)
val kokeilu = luvut.map( n => Vector(-n.abs, 0, n.abs) )kokeilu: Vector[Vector[Int]] = Vector(Vector(-10, 0, 10), Vector(-5, 0, 5), Vector(-4, 0, 4), Vector(-5, 0, 5),
Vector(-20, 0, 20))
kokeilu.flattenres15: Vector[Int] = Vector(-10, 0, 10, -5, 0, 5, -4, 0, 4, -5, 0, 5, -20, 0, 20)

"Mäppäyksen" ja litistämisen voi yhdistää:

luvut.flatMap( n => Vector(-n.abs, 0, n.abs) )res16: Vector[Int] = Vector(-10, 0, 10, -5, 0, 5, -4, 0, 4, -5, 0, 5, -20, 0, 20)

Käsky kokoelma.flatMap(funktio) siis ajaa saman asian kuin kokoelma.map(funktio).flatten.

Saatat ihmetellä, onko moiselle tosiaan niin paljon tarvetta, että erillisestä flatMap-yhdistelmämetodista on hyötyä. On sille. Metodin hyödyllisyys korostuu, kun ohjelmointikokemuksesi karttuu tämän kurssin aikana ja sen jälkeen.

Esimerkki: käyttäjiä ja osoitteita

Äskeistä hieman kiinnostavampia esimerkkejä map- ja flatMap-metodeista saadaan, kun tarkastelemme seuraavaa pientä luokkaa.

class Kayttaja(val tunnus: String, val mailiosoitteet: Vector[String]):
  override def toString = this.tunnus + " <" + this.mailiosoitteet.mkString(",") + ">"

Oletetaan nyt, että ohjelma käsittelee useita tällaisia käyttäjiä, jotka on tallennettu vektoriin. Seuraavassa esimerkkikoodissa käyttäjäolioita luodaan vain kaksi, mutta niitä voisi olla kuinka paljon tahansa.

val kaikkiKayttajat = Vector(
  Kayttaja("taina", Vector("taina.teekkari@aalto.fi", "taina.teekkari@iki.fi", "taina.teekkari@gmail.com")),
  Kayttaja("megadestroyer", Vector("teemu.teekkari@aalto.fi", "teemuteekkari@gmail.com"))
)kaikkiKayttajat: Vector[Kayttaja] =
Vector(taina <taina.teekkari@aalto.fi,taina.teekkari@iki.fi,taina.teekkari@gmail.com>,
megadestroyer <teemu.teekkari@aalto.fi,teemuteekkari@gmail.com>)

Mitä, jos halutaan selvittää kaikkien vektoriin tallennettujen käyttäjien käyttäjätunnukset? Tai muodostaa vektori, jossa on kaikkien käyttäjien kaikki sähköpostiosoitteet?

Silmukoita voisi tietysti käyttää, mutta mainituilla korkeamman asteen metodeilla homma onnistuu vaivatta.

Kaikkien käyttäjien käyttäjätunnukset saadaan kauniisti map-metodilla, kun parametriksi annetaan funktio, joka "mäppää" olion sen tunnus-ilmentymämuuttujan arvoksi.

kaikkiKayttajat.map( _.tunnus )res17: Vector[String] = Vector(taina, megadestroyer)

Pelkällä map-metodilla saadaan myös sähköpostiosoitteet. Ne tulevat sisäkkäisessä kokoelmassa, mikä ei (tarkoituksesta riippuen) välttämättä ole kätevää:

kaikkiKayttajat.map( _.mailiosoitteet )res18: Vector[Vector[String]] = Vector(Vector(taina.teekkari@aalto.fi, taina.teekkari@iki.fi, taina.teekkari@gmail.com),
Vector(teemu.teekkari@aalto.fi, teemuteekkari@gmail.com))

Käyttämällä mapin sijaan flatMap-metodia saadaan haluttu "litteä" luettelo kaikista kaikkien käyttäjien sähköpostiosoitteista:

kaikkiKayttajat.flatMap( _.mailiosoitteet )res19: Vector[String] = Vector(taina.teekkari@aalto.fi, taina.teekkari@iki.fi, taina.teekkari@gmail.com,
teemu.teekkari@aalto.fi, teemuteekkari@gmail.com)

Seuraava ohjelmointiharjoitus ei käsittele pelkästään äskeisiä kokoelmien metodeita, mutta niillekin löytyy käyttöä.

Tehtävä: matopeli

Matopeli (Snake) on alun perin 1970-lukulainen klassikko, jossa pelaajan ohjaama "mato" tai "käärme" kääntyilee kaksiulotteisella kentällä ja etsii syötävää kasvaakseen. 1990-luvulla se teki näyttävän paluun kännyköihin, millä on viime vuosinakin retroiltu. Tätä lukiessasi peli saattaa jo olla uusioretrokitschiä.

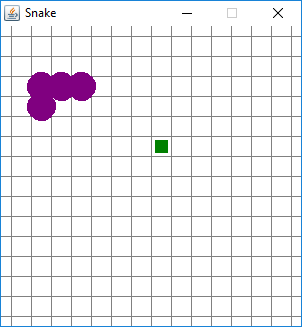
../_images/snake_on_grid_1.png

Matopeli ja sen toimintaa selkiyttävä ruudukko. Vihreä neliö kuvaa madolle seuraavaksi tarjolla olevaa ruokaa; se on ruudussa numero (8,6). Numerointi alkaa vasemman yläkulman ruudusta (0,0); se kuten muutkin reunaruudut näkyvät kuvassa vain osittain. Kuvan mato muodostuu neljästä segmentistä, jotka sijaitsevat ruuduissa (5,4), (4,4), (3,4) ja (3,5).

Ohjelmointiharjoituksenakin matopeli on klassinen. Yhtykäämme perinteeseen.

Matopelin käsitteitä

Matopelin keskeiset osat ovat itse mato sekä ruoka, jota mato etsii. Kullakin hetkellä tarjolla on yksi ruoka jossakin päin pelikenttää. Kun mato syö sen eli madon pää on osumassa ruokaan, mato kasvaa ja pelikentälle ilmestyy uusi ruoka.

Pelialueen voi mieltää ruudukoksi (grid), jossa ruoka sijaitsee tietyssä ruudussa (ks. kuva). Mato koostuu "pätkistä" eli segmenteistä, joista kukin sijoittuu tiettyyn ruutuun.

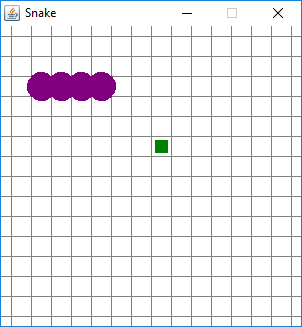
../_images/snake_on_grid_2.png

Ensimmäinen kuva oli tilanteesta, jossa mato oli ollut matkalla ylös ja kääntynyt oikealle. Tässä toisessa kuvassa mato on liikkunut yhden lisäaskelen edelliseen verrattuna. Madon etupää on siirtynyt ruudun verran oikealle ja "vetänyt perässään" muita kolmea. Ruutu (3,5), jossa madon viimeinen segmentti oli, jäi tyhjäksi.

Pelaajan ainoa toimi on kääntää madon liikkumasuuntaa nuolinäppäimillä. Suuntana voi olla jokin neljästä pääilmansuunnasta.

Pelin edetessä mato liikkuu: sen pää eli etummainen segmentti liikkuu viimeisimpään pelaajan valitsemaan suuntaan ja muut segmentit seuraavat perässä (ks. toinen kuva). Kuitenkin jos madon pää osuu ruokaan, mato syö sen ja kasvaa yhdellä segmentillä: ruoan kohdalle ilmestyy uusi segmentti ja kaikki aiemmat jäävät entiselleen.

Peli päättyy, kun madon pää osuu johonkin muuhun kuin ruokaan.

Snake-ohjelman luokat

Moduulissa Snake on osittainen toteutus matopelille. Sen kokonaisrakenne on samankaltainen kuin tutussa FlappyBug-ohjelmassa: SnakeGame-luokalla mallinnetaan pelitilanteita, ja SnakeApp.scala määrittelee käyttölittymän, joka pistää pelitilanteen näkyviin ja vastaanottaa pelaajan komennot.

Luokan SnakeGame ilmentymä on siis yksi matopelisessio. Tuollainen olio on muuttuvatilainen: sen tila muuttuu, kun sen metodeita kutsutaan. SnakeGame-olio pitää kirjaa

  • seuraavasta tarjolla olevasta ruuasta: missä päin ruudukkoa se on?

  • madon segmenttien sijainneista: missä päin ruudukkoa ne ovat?

  • madon (pään) kulkusuunnasta: mihin neljästä pääsuunnasta se on viimeksi asetettu kulkemaan?

Luokan pitää siis käsitellä sijainteja ruudukolla sekä suuntia. Näihin tarpeisiin löytyy välineitä o1-kirjastostamme:

Apuluokkia: GridPos ja CompassDir

Luokka GridPos sopii kuvaamaan kahdesta kokonaisluvusta koostuvia koordinaatteja ruudukossa.

  • Se on samantapainen kuin tuttu Pos, mutta edustaa nimenomaan ruudukkokoordinaatteja ja tarjoaa siihen tarkoitukseen sopivia metodeita.

  • Näin erotamme toisistaan kaksi seikkaa: sen, missä ruudussa asia on (GridPos), ja sen, mihin pisteeseen tietynkokoisessa kuvassa tuo asia piirretään (Pos).

    • Ruudukkosijainti on osa aihealueen logiikkaa (matopelin sääntöjä). Sijainti kuvassa liittyy vain käyttöliittymään.

    • Vrt. Stars-ohjelma, jossa erotimme toisistaan StarCoords-sijainnin kartalla ja Pos-sijainnin kuvassa.

Luokka CompassDir kuvaa "ilmansuuntia" kuten pohjoinen (eli ylös) tai länsi (eli vasemmalle).

  • Se sopii hyvin madon liikkumasuunnan kirjaamiseen.

  • Se toimii hyvin yhteen GridPos-luokan kanssa. Voimme esimerkiksi kysyä tiettyä GridPos-oliolta, joka vastaa tiettyä koordinaattiparia, mikä sen itäinen naapurikoordinaatti on.

Molempien luokkien Scaladoc-dokumentaatio löytyy O1Library-moduulista.

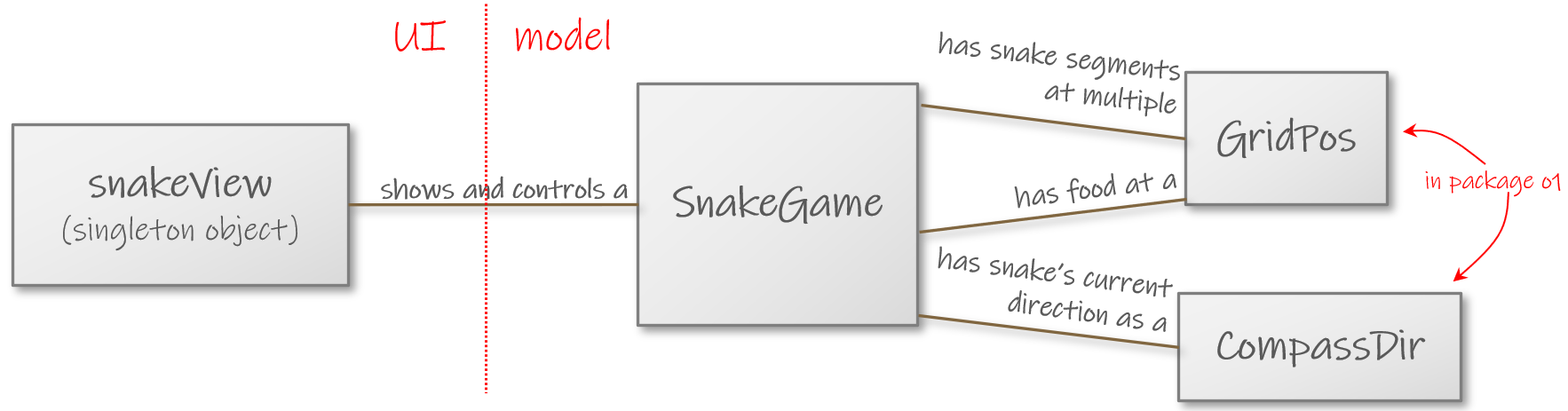
../_images/module_snake.png

Snake-ohjelmaan liittyvien luokkien väliset yhteydet.

Ensin pari pohjustavaa pikkutehtävää

Näiden parin pikkukysymyksen vastauksista on hyötyä varsinaisessa matopelitehtävässä.

A+ esittää tässä kohdassa tehtävän palautuslomakkeen.

A+ esittää tässä kohdassa tehtävän palautuslomakkeen.

Varsinainen tehtävänanto

Toteuta tiedostoihin SnakeGame.scala ja SnakeApp.scala puuttuviksi merkityt kohdat. Suosittelemme seuraavaa järjestystä.

Vaihe 0/5: valmistelut

Aja annettu ohjelma. Esiin tulee pelimaailma, jossa on ruoka ja yhden segmentin mittainen matonen. (Yllä oleviin kuviin lisäksi piirretyn ruudukon ei ole tarkoituskaan näkyä.) Mato ei vielä liiku.

Tutustu SnakeGame-luokkaan. Paikanna puuttuvat osat. Katso, miten annettu koodi käyttää GridPos- ja CompassDir-luokkia. Lue noiden kahden luokan Scaladoc-dokumentaatiosta ainakin alun johdannot; kaikkia metodeita ei ole tarpeen opetella. (Itse Snake-moduulista ei ole scaladoceja, vaan tarvittavat tiedot on annettu tässä luvussa ja koodissa.)

Voit silmäillä käyttöliittymääkin. Se on laadittu niin, että se kutsuu SnakeGame-olion advance-metodia kellon tikittäessä (onTick). advance-metodin pitäisi liikuttaa matoa; annettu versio metodista ei kuitenkaan tee mitään.

Vaihe 1/5: mato liikkeelle

Toteuta advance ensin osittaisena: laita se siirtämään madon pää viereiseen ruutuun. Älä vielä välitä madon kasvattamisesta tai ruoan sijainnista.

Huomaa: segments-muuttuja osoittaa yksialkioiseen vektoriin, jossa on madon (pään) sijainti. Kyseessä on var-muuttuja. advance-metodin tulee korvata entinen vektori uudella, jossa on vanhan sijainnin naapureista se, joka on madon kulkusuunnassa.

Esimerkki: segments-muuttuja osoittaa vektoriin, joka ainoana alkiona on koordinaatteja (2, 4) vastaava GridPos-olio. Mato on menossa oikealle. Kun advancea kutsutaan, metodin tulee vaihtaa segments-muuttujan arvoksi uusi vektori, jossa on (ainoana alkiona) koordinaatteja (3, 4) vastaava GridPos-olio.

Naapurin saa kätevästi GridPos-luokan metodilla.

Aja muokattu ohjelma. Yksisegmenttisen madon pitäisi nyt vipeltää ruudulla. Peli päättyy sen törmätessä pelialueen reunaan. Nuolinäppäimet (tai WASD-näppäimet) ohjaavat matoa. Mato menee läpi ruoista niitä nauttimatta.

Vaihe 2/5: ruoka

Kehitä advance-metodia edelleen. Metodin on nyt lisäksi arvottava ruoalle uusi sijainti aina kun mato osuu ruokaan. Tämä tapahtuu osana samaa liikettä (eli osana samaa advance-kutsua), joka siirtää madon ainoan segmentin ruoan kohdalle. Metodi siis ensin siirtää matoa ja sitten ruokaa; näistä jälkimmäinen tehdään vain madon päätyessä ruoan kohdalle.

Tämä käy vaihtamalla pelin nextFood-muuttujan arvoa. Tarjolla on metodi randomEmptyLocation(), jolla voit arpoa uuden sijainnin. (Se on SnakeGamen metodi. Metodin toteutusta ei tarvitse ymmärtää; riittää kun kutsut sitä ja käytät sen palauttamaa GridPos-arvoa.)

Pelin nopeus on määritelty käyttöliittymän vakiossa GameSpeed. Voit säätää sitä mielesi mukaan. Jos peliä testatessasi vaihdat nopeudeksi esimerkiksi 1, niin aika matelee hyvin hitaasti.

Vaihe 3/5: kasvu

Laitetaan mato kasvamaan. Huomaa kuitenkin, että tässä vaiheessa muokkaat vasta ohjelman sisäistä mallia madon tilasta — et vielä käyttöliittymää. Kasvu ei siis vielä näy ruudulla, joten älä ihmettele, jos et nyt saa näkyvää muutosta peliin.

Viimeistele advance-metodi. Metodin tulee joka kutsukerralla joko kasvattaa tai liikuttaa matoa, muttei molempia näistä. Tapauksia on kaksi: kun pää on osumaisillaan ruokaan, mato syö ja siihen lisätään segmentti; muussa tapauksessa mato etenee saman kokoisena kuin ennenkin.

Edellisessä vaiheessa oletettiin, että segments-muuttujan osoittamassa vektorissa on aina tasan yksi alkio. Nyt tämä oletus ei enää päde.

Yllä vaiheessa 1 kirjoitit koodirivin, joka päivittää segments-muuttujan arvoksi uuden yksialkioisen vektorin. Poista tuo käsky. Kirjoita sen tilalle uutta koodia, joka käsittelee kummankin tapauksista: ruokaan osuttiin tai ei osuttu.

Toisin sanoen: korvaa segments-muuttujan vanha arvo uudella vektorilla, jossa on kaikki madon segmenttien uudet sijainnit. Segmenttejä tulisi olla askelen jälkeen joko yhtä monta kuin ennen tai yksi enemmän.

Ohjeita ja vinkkejä:

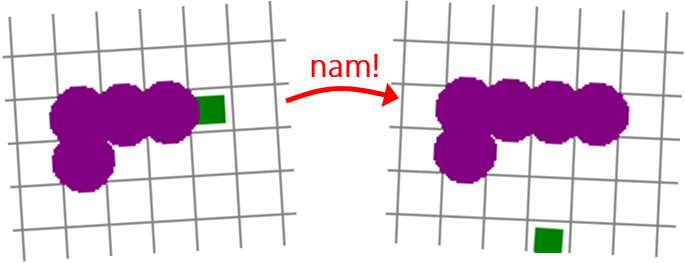
../_images/snake_on_grid_3-fi.png

Vasen kuva on hetkestä juuri ennen kuin mato syö ruoan, joka on sen pään edessä. Oikealla kello on naksahtanut kerran ja ruoka syöty: muut segmentit ovat paikallaan, mutta niiden eteen on ilmestynyt uusi segmentti madon uudeksi etupääksi. Ruokaa on samalla ilmestynyt toisaalle.

  • Kasvata matoa etupäästä. Kun madon pää muuten etenisi ruoan kohdalle, älä liikuta mitään segmenttiä vaan lisää eteen ruoan tilalle yksi segmentti uudeksi pääksi. (Aiemmin etummaisena ollut segmentti jää toiseksi. Myös viimeinen segmentti säilyy paikoillaan. Ks. oheinen kuvapari.)

  • Ruoan on siirryttävä uuteen sijaintiin osana samaa advance-kutsua, joka tuo madon pään ruoan kohdalle. (advance-kutsun päättyessä ruoka ei koskaan ole madon pään kohdalla.)

  • Uuden vektorin muodostamisessa voit hyödyntää luvun 4.1 esittelemiä työkaluja, joita tuossa yllä pikkutehtävissä kerrattiin.

    • Segmentit ovat identtisiä. Jokaista segmenttiä ei tarvitse erikseen siirtää. Kaikki keskimmäiset segmentit säilyvät osana matoa; näennäinen liike syntyy, kunhan huolehdit madon etu- ja peräpäästä.

    • Alla on lisävinkki, jotka voit paljastaa halutessasi.

      Vinkki madon segmenttien siirtämiseen

      Madon edetessä syömättä sinun on muodostettava uusi vektori, jossa on madon pään uuden sijainnin lisäksi kaikki madon aiemmat sijainnit paitsi viimeinen. Idea on ihan sama kuin yllä pikkutehtävässä, jossa liitettiin vektorin alkuun uusi luku.

      Muista, että pelkkä vektorin luominen ei pistä tuota uutta vektoria mihinkään talteen, vaan se pitää hoitaa sijoituskäskyllä.

Kokeile ohjelmaa tämän vaiheen lopuksi. Mato ei edelleenkään näytä kasvavan. Kasvaa se kyllä, mutta kasvu ei näy, koska käyttöliittymä ei piirrä näkyviin kuin madon pään.

Vaihe 4/5: grafiikka kuntoon

Siirry käyttöliittymään ja siellä makePic-metodiin. Huomaa:

  • Metodi lisää taustaa vasten vain yhden kappaleen SegmentPic-kuvaa (punertavaa madonosaa).

  • makePic käyttää samassa tiedostossa määriteltyä apufunktiota toPixelPos määrittääkseen ruudukkokoordinaattien perusteella pikselin, johon SegmentPic piirtyy.

  • makePicin käyttämä Pic-luokan metodi placeCopies ottaa ensimmäiseksi parametrikseen kuvan ja toiseksi vektorillisen sijainteja (Pos-olioita). Se toimii kuten tuttu place-metodi mutta sijoittaa taustaa vasten useita kopioita samasta kuvasta. Annettu koodi tosin antaa tuolle metodille parametriksi aina vain yksialkioisen vektorin.

Muokkaa makePic-metodia niin, että se piirtää kaikki madon segmentit identtisinä palluroina. Se käy näin:

  • Määritä kunkin segmentin kuvan sijainti toPixelPos-metodilla. Et tarvitse silmukkaa. Käytä apuna tämän luvun esittelemää kokoelmametodia.

    Vinkki

    Kokoelmassa on GridPos-sijainteja. Kokoelman, jossa on kutakin niistä vastaava Pos, saat map-metodikutsulla.

  • Anna placeCopies-metodille vektori, jossa ovat kaikki segmenttien sijainnit Pos-olioina.

Mato kasvaa!

Vaihe 5/5: törmäykset

Matopelien perinteeseen kuuluu, että mato voi törmätä paitsi seiniin myös itseensä. Huomioi tämä SnakeGame-luokan isOver-metodissa: pelin pitää päättyä myös, jos madon pää on päätynyt samaan ruutuun jonkin muun segmentin kanssa. (Siis vasta silloin, jos pään sijainti on jo sama kuin jonkin muun segmentin.)

Luvusta 4.1 löytyy taas työkaluja.

Vinkki

Madolla on pää ja häntä. Metodisi tulee tutkia, onko päässyt käymään niin, että pään sijainti on hännän sijaintien joukossa eli häntä sisältää pään. Kuten sanottu, työkalut juuri tuohon löytyvät luvusta 4.1.

Erikoistapaus

Mitä pitäisi tapahtua, kun täsmälleen kaksisegmenttinen mato kääntyy 180 astetta? Ehtiikö häntä pois pään alta vai ei? Vai pitäisikö suora käännös taaksepäin kokonaan estää? Saat itse päättää; tehtävän automaattitesti ei huomioi tätä tapausta.

A+ esittää tässä kohdassa tehtävän palautuslomakkeen.

Yhteenvetoa

  • Kokoelmille on Scala-kielen peruskirjastoissa määritelty koko joukko korkeamman asteen metodeita, joilla kokoelmien sisältöä voi käsitellä.

    • Yleisesti käytettyjä korkeamman asteen metodeita ovat mm. foreach, exists, forall, find, filter, map ja flatMap. Lisää kohtaamme myöhemmin.

    • Nämä metodit tarjoavat käteviä ratkaisuvaihtoehtoja moniin sellaisiin tilanteisiin, joissa silmukan käyttö olisi toinen vaihtoehto.

    • Tällainen kokoelmien käsittely on erityisen yleistä ns. funktionaalisessa ohjelmoinnissa, jota Scala voimakkaasti tukee.

  • Lukuun liittyviä termejä sanastosivulla: korkeamman asteen funktio; kokoelma; abstraktiotaso.

Tämän luvun merkityksestä

Useat tämän luvun esittelemistä metodeista ovat runsaassa käytössä tulevissa luvuissa. Niiden tunteminen helpottaa monien tulevien harjoitustehtävien tekemistä. Lisäksi sinun on kyettävä lukemaan annettua ohjelmakoodia, jossa näitä metodeita käytetään.

Kaikkien uusien metodien muistaminen ei varmasti heti onnistu, mutta ei tarvitsekaan. Voit palata kertaamaan esimerkiksi metodien nimiä ja muita yksityiskohtia tästä luvusta tai Scalaa kootusti -sivulta.

Tärkeintä on nyt muistaa perusajatus: kokoelmia voi käsitellä korkeamman asteen metodeilla, ja tarjolla on laaja valikoima erilaisia näppäriä metodeita.

Maistiainen: for–yield-lausekkeet

Mainituksi jo tulikin, että käyttämämme for–do-silmukat ovat vain toinen tapa kirjoittaa foreach-metodikutsu. Nämä siis tekevät saman:

lukuja.foreach( luku => println("Neliö on " + luku * luku) )

for luku <- lukuja do
  println("Neliö on " + luku * luku) )

Scalan for-rakenteella voi tehdä monenlaista muutakin (vaikkei O1:llä tarvitsekaan). Myös map-kutsun voi kirjoittaa for-sanaa käyttäen. Nämä tekevät saman:

val neliot = lukuja.map( luku => luku * luku )

val neliot = for luku <- lukuja yield luku * luku

yield on varattu sana, jolla for-lausekkeen saa tuottamaan muutakin kuin Unit.

Alla on puolestaan flatMap-kutsu sekä sen kanssa saman asian tekevä for–yield-lauseke. Kumpikin esimerkkikoodi käy lukuvektorin läpi kahdesti ja tuottaa kaikki mahdolliset kahden alkion summat.

val summat = for eka <- lukuja; toka <- lukuja yield eka + toka

val summat = lukuja.flatMap( eka => lukuja.map( toka => eka + toka ) )

for–yield-lausekkeen voi jaotella riveiksi esimerkiksi näin:

val summat =
  for
    eka  <- lukuja
    toka <- lukuja
  yield eka + toka

Palaute

Huomaathan, että tämä on henkilökohtainen osio! Vaikka olisit tehnyt lukuun liittyvät tehtävät parin kanssa, täytä palautelomake itse.

Tekijät

Tämän oppimateriaalin kehitystyössä on käytetty apuna tuhansilta opiskelijoilta kerättyä palautetta. Kiitos!

Materiaalin luvut tehtävineen ja viikkokoosteineen on laatinut Juha Sorva.

Liitesivut (sanasto, Scala-kooste, usein kysytyt kysymykset jne.) on kirjoittanut Juha Sorva sikäli kuin sivulla ei ole toisin mainittu.

Tehtävien automaattisen arvioinnin ovat toteuttaneet: (aakkosjärjestyksessä) Riku Autio, Kai Bukharenko, Nikolas Drosdek, Kaisa Ek, Rasmus Fyhrqvist, Joonatan Honkamaa, Antti Immonen, Jaakko Kantojärvi, Onni Komulainen, Niklas Kröger, Kalle Laitinen, Teemu Lehtinen, Mikael Lenander, Ilona Ma, Jaakko Nakaza, Strasdosky Otewa, Kaappo Raivio, Timi Seppälä, Teemu Sirkiä, Onni Tammi, Joel Toppinen, Anna Valldeoriola Cardó ja Aleksi Vartiainen.

Lukujen alkuja koristavat kuvat ja muut vastaavat kuvituskuvat on piirtänyt Christina Lassheikki.

Yksityiskohtaiset animaatiot Scala-ohjelmien suorituksen vaiheista suunnittelivat Juha Sorva ja Teemu Sirkiä. Teemu Sirkiä ja Riku Autio toteuttivat ne apunaan Teemun aiemmin rakentamat työkalut Jsvee ja Kelmu.

Muut diagrammit ja materiaaliin upotetut vuorovaikutteiset esitykset laati Juha Sorva.

O1Library-ohjelmakirjaston ovat kehittäneet Aleksi Lukkarinen, Juha Sorva ja Jaakko Nakaza. Useat sen keskeisistä osista tukeutuvat Aleksin SMCL-kirjastoon.

Tapa, jolla käytämme O1Libraryn työkaluja (kuten Pic) yksinkertaiseen graafiseen ohjelmointiin, on saanut vaikutteita tekijöiden Flatt, Felleisen, Findler ja Krishnamurthi oppikirjasta How to Design Programs sekä Stephen Blochin oppikirjasta Picturing Programs.

Oppimisalusta A+ luotiin alun perin Aallon LeTech-tutkimusryhmässä pitkälti opiskelijavoimin. Nykyään tätä avoimen lähdekoodin projektia kehittää Tietotekniikan laitoksen opetusteknologiatiimi ja tarjoaa palveluna laitoksen IT-tuki; sitä ovat kehittäneet kymmenet Aallon opiskelijat ja muut.

A+ Courses -lisäosa, joka tukee A+:aa ja O1-kurssia IntelliJ-ohjelmointiympäristössä, on toinen avoin projekti. Sen suunnitteluun ja toteutukseen on osallistunut useita opiskelijoita yhteistyössä O1-kurssin opettajien kanssa.

Kurssin tämänhetkinen henkilökunta löytyy luvusta 1.1.

Joidenkin lukujen lopuissa on lukukohtaisia lisäyksiä tähän tekijäluetteloon.

a drop of ink
Palautusta lähetetään...