Kvanttitietokoneen uhat¶
Tähän asti kurssilla esitetyt arviot eri salausmenetelmien turvallisuudesta ovat perustuneet perinteisten tietokoneiden laskentatehoon. Kvanttitietokoneet muuttavat näitä oletuksia – joissain tapauksissa niin merkittävästi, että nykyisin käytössä olevat salausmenetelmät ovat tehokkaita kvanttitietokoneita vastaan täysin turvattomia. Vaikka tällä hetkellä, vuonna 2022, kvanttitietokoneet eivät vielä ole tarpeeksi kehittyneitä murtamaan kryptografisia järjestelmiä, niiden uhka kryptografialle ei ole pelkästään teoreettinen. Tämän takia kryptologit ovatkin suunnitelleet kvanttiturvallisia salausmenetelmiä jo yli kymmenen vuotta.
Tällä kursilla emme kuitenkaan käsittele kvanttisalausta, joka on aivan oma tutkimusalansa. Voit kuitenkin lukea aiheesta kvanttikryptografian Wikipedia-artikkelista.
”Klassiset” kvanttitietokonealgoritmit¶
Kvanttitietokoneiden luoma uhka tällä hetkellä käytössä oleville salauksille johtuu pitkälti kahdesta jo 1990-luvulla kehitetystä kvanttialgoritmista:
Groverin algoritmi
Shorin algoritmi
Näitä algoritmeja voidaan leikkisästi kutsua ”klassisiksi”, koska ne ovat nykyisen kryptografian kehityksen kannalta jo hyvinkin vanhoja keksintöjä.
Näiden algoritmien avulla kvanttitietokone pystyisi ratkaisemaan tiettyjä matemaattisia ongelmia huomattavasti perinteistä tietokonetta nopeammin. Kryptografian kannalta algoritmeilla on kuitenkin hyvinkin erilaisia seuraamuksia.
Groverin algoritmi¶
Tietojenkäsittelytieteilijä Lov Groverin vuonna 1996 kehittämän Groverin algoritmin avulla kvanttitietokone pystyy suorittamaan algoritmisen etsinnän merkittävästi perinteistä tietokonetta nopeammin.
Mitä tarkoittaa etsiminen? Kuvitellaan tilanne, jossa sinulla on tallennettuna kaikkien tuntemiesi ihmisten nimet ja puhelinnumerot erilillisille paperilapulle. Jos kaikki paperilaput laitetaan hattuun ja ne sekoitetaan, kauanko sinulta kestää löytää tietyn ystäväsi, esimerkiksi Alicen, puhelinnumero? Joudut nostamaan lappuja hatusta niin pitkään, että kohdallesi osuu paperilappu jossa on Alicen nimi ja puhelinnumero. Jos paperilappujen määrä on \(N\), parhaassa tapauksessa ensimmäinen nostamasi paperilappu voi olla etsimäsi. Huonoimmassa tapauksessa se on viimeinen.
Odotusarvo on, että joudut tekemään keskimäärin \(\frac{N}{2}\) nostoa löytääksesi oikean lapun.
Groverin algoritimilla tarvitaan vain \(\sqrt{N}\) nostoa, että oikea lappu löytyy.
Jos hatussa on 100 lappua, tavallisella etsinnällä oletamme että se löytyy 50:llä nostolla. Groverin algoritmilla se löytyisi 10:llä nostolla.
Jos sinulla on \(2^{128}\) lappua, niin tavallisella etsinnällä 50 % todennäköisyys löytää etsimäsi lappu vaatisi \(2^{127}\) nostoa. Groverin algoritmilla vaadittava määrä olisi \(\sqrt{2^{128}}=2^{64}\) nostoa.
Huomaatko valtavan eron laskentatarpeessa, kun lähtökohtana on vaativammat ongelmat?
Paperilappujen sijaan Groverin algoritmille annetaan syöte ja funktio, ja algoritmi osaa päätellä esimerkiksi funktion tai sen käänteisfunktion. Tiivisteistä muistamme, että niissä käytetään yksisuuntaisia funktioita, joista on käytännössä mahdotonta luoda käänteisfunktiota. Groverin algoritmilla kuitenkin on mahdollista toteuttaa tällainen käänteisfunktio, jolloin halutessaan on mahdollista myös tuottaa alkukuva, joka aiheuttaa esimerkiksi tiivisteiden törmäyksen.
Toinen kryptografian kannalta oleellinen Groverin algoritmin sovellus on, että opetusmoduulissa 4 käsitellyn brute-force-hyökkäyksen tehokkuus parantuu huomattavasti, kun sen suorittaa kvanttitietokoneella. Groverin algoritmin avulla hyökkääjä pystyisi murtamaan 128-bittisen avaimen suunnilleen \(2^{64}\) iteraatiossa. Vertailun vuoksi, vuonna 2021 hajautettu virtuaalivaluttojen eli bitcoinien laskenta pystyi laskemaan vuorokaudessa \(2^{83}\) tiivistettä.
Näin ollen erityisesti symmetriset salausmenetelmät ja tiivistefunktiot ovat alttiita Groverin algoritmilla tehdyille hyökkäyksille. Nykyisen ymmärrykseen mukaan avaimien pituuksien kaksinkertaistaminen olisi riittävä suojautumiskeino Groverin algoritmia vastaan.
Shorin algoritmi¶
Matemaatikko Peter Shorin vuonna 1994 julkaiseman Shorin algoritmin avulla kvanttitietokone pystyy ratkaisemaan diskreettien logaritmien löytämiseen ja kokonaislukujen tekijöihin jakamiseen liittyvät ongelmat eksponentiaalisesti nopeammin kuin perinteinen tietokone.
Tämän kokoluokan nopeutus tarkoittaa sitä, että opetusmoduulissa 7 käsitellyt perinteiset julkisen avaimen salausmenetelmät, RSA ja Diffie–Hellman, ovat täysin turvattomia tehokasta kvanttitietokonetta vastaan. RSA:n turvallisuus perustuu siihen, että suurien alkulukujen tulo on vaikea jakaa tekijöihin. Diffie-Hellman-protokollan turvallisuus puolestaan perustuu diskreettien logaritmien laskemisen vaikeuteen. Muistat varmaan seuraavan kuvan, jossa luku jaettiin tekijöihin suurella laskentakapasiteetilla.
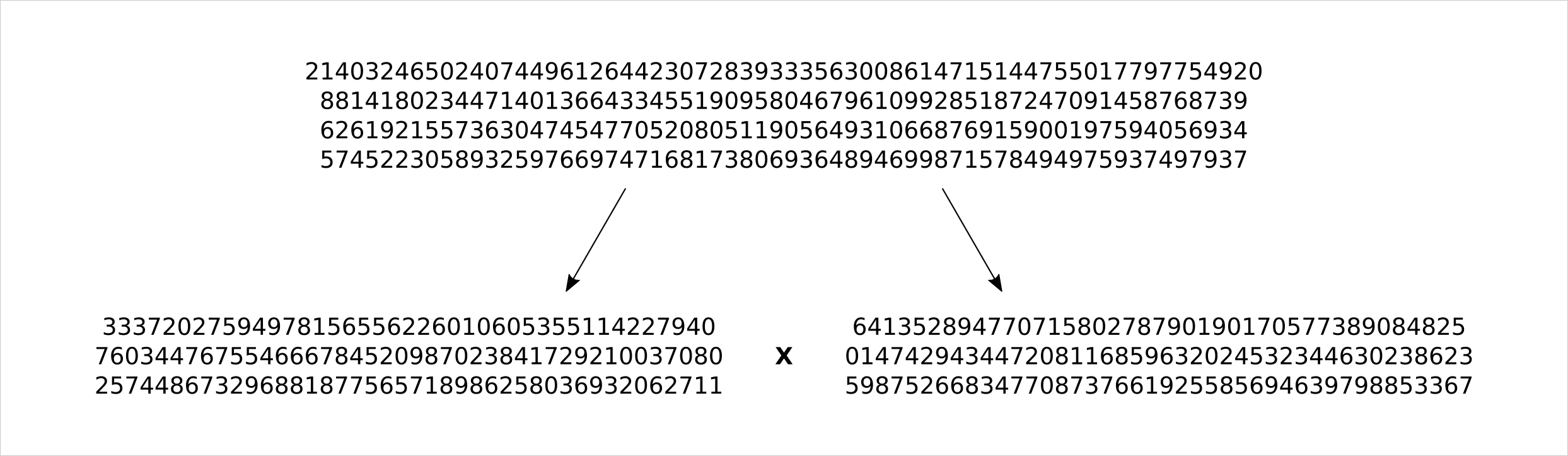
Shorin algoritmin aiheuttaman uhan vuoksi kryptologit ovat kehittäneet kvanttiturvallisia kryptografisia algoritmeja, joiden murtamiseen ei ole vielä löytynyt kvanttialgoritmia. Tulevaisuudessa erityisesti julkisen avaimen menetelmät tulevat hyvin todennäköisesti perustumaan näihin kvanttiturvallisiin algoritmeihin, jotka ovat aktiivinen tutkimuskohde tällä hetkellä. Ensimmäiset prosessit kvanttiturvallisten julkisen avaimen menetelmien standardoimiseksi ovat jo parhaillaan käynnissä. Voidaankin olettaa, että kun ensimmäiset standardit tulevat valmiiksi lähivuosina, niin enenevissä määrin nykyiset julkisen avaimen menetelmät alkavat korvautua vastaavilla kvanttiturvallisilla menetelmillä.
Voimme vain toivoa, että siirtyminen kvanttiturvallisiin salaimiin saadaan päätökseen ennen kuin laajamittainen kvanttilaskenta tulee mahdolliseksi! Onhan myös mahdollista, että joku taho nauhoittaa tänään digitaalista dataa ja käyttää kvanttitietokoneita myöhemmin informaation avaamiseksi tai muuttamiseksi.
Lisätietoa¶
Jos haluat lukea kvanttilaskennasta lisää, on ilmainen Qiskit siihen aivan erinomainen lähde. Qiskitin koodialusta toimii myös Pythonilla. Sivuston sisältö ylittää reippaasti jopa joidenkin yliopistokurssien sisällön, mutta materiaali on tällä hetkellä selkein kuvaus siitä, mistä kvanttilaskennassa on kyse.
Kvanttilaskennan jälkeinen kryptografia¶

Kvanttilaskennan jälkeinen kryptografia (engl. Post Quantum Cryptograpy - PQC) on kiinnostava aihe, jota on tutkittu lähes 20 vuotta ja jonka tutkimus ja kehitys jatkuvat edelleen. Kvanttilaskenta-algoritmeihin ja kvanttitietokoneisiin on investoitu merkittävästi ja oletettavaa on, että kumpikin osa-alue tulee kehittymään huomattavasti seuraavan kahden vuosikymmenen aikana.
Kuten aiemmin mainittiin, kryptologit ovat kehittäneet runsaasti kvanttilaskentaa kestäviä menetelmiä: symmetrisiä ja epäsymmetrisiä funktioita (julkinen avain) sekä tiivistefunktioita. Aivan kuin AES valikoitui aikoinaan standardiksi NIST:n järjestämän kilpailun seurauksena, on tällä hetkellä käynnissä kilpailu PQC-algoritmien standardoinniksi.
Kannattaa siis seurata, mikä algoritmi tai algoritmit valikoituvat PQC-kilpailun voittajiksi. Voit verrata näiden voittaja-algorimien toimintaa nykyisiin salausalgoritmeihin, joiden toiminnan tunnet jo kohtuullisen hyvin.
Yhteenveto¶
Kvanttilaskenta vaarantaa osan nykyisin käytettävistä kryptografisista menetelmistä. Siksi nykyisiä algoritmeja on muokattava niin, että ne kestävät tulevat vuosikymmenet jossa kvanttilaskenta on todellisuutta.
Seuraavaksi katsomme, mitä kryptografian aihealueita kryptologit tutkivat juuri nyt.