1. CS-EJ4404
  2. 6. Lohkosalaimen käyttö
  3. 6.4 Lohkosalaimen laskuritila

Lohkosalaimen laskuritila

Miten voimme salata tietoa, jos se on esimerkiksi suoratoistettavaa dataa kuten videota tai ääntä? Kun käytetään tässä moduulissa aikaisemmin esiteltyjä toimintamoodeja, lohkosalain pilkkoo datan, salaa sen ja lähettää kaiken salatun datan yhdellä kertaa. Jatkuvan datavirran suojaamiseen tarvitaan jonosalainta. Lohkosalain toimii jonosalaimena laskuritilassa (eng. counter) eli CTR-moodissa.

Kun muodostetaan AES-salaimeen pohjautuvaa jonosalainta, osapuolten on ensin sovittava avain, aivan kuten aiemmin. Sen lisäksi osapuolten on vaihdettava tieto salaustapahtuman kertakäyttöluvusta \(N\) ja sovittava millaista laskuria käytetään.

Tarvitsemme siis:

  • Avaimen \(K\)

  • Kertakäyttöluvun \(N\)

  • Laskurin \(Ctr\)

Laskuri

Kuvissa näkyy symboli ||. Se tarkoittaa että kertakäyttöluvun perään lisätään laskurin arvo. Kaksi numeroa siis yhdistetään eli puhekielisesti konkatenoidaan. Katsotaan esimerkkitapausta, jossa:

  • Lohkosalaimessa on 16-bittiset lohkot.

  • Kertakäyttöluvun \(N\) pituus on 8 bittiä.

  • Kertakäyttöluvun tämän yhteyskerran arvoksi asetetaan \(N=0x4A\)

  • Myös laskurin \(Ctr\) pituus myös on 8 bittiä.

  • Laskuri laskee nollasta 255:een, eli heksana 0x00:sta 0xFF:ään.

Tällöin lohkosalain saa syötteksi seuraavat konkatenoidut arvot:

  • \(N+Ctr\) , eli 0x4A00

  • \(N+Ctr+1\) , eli 0x4A01

  • \(N+Ctr+2\) , eli 0x4A02

  • …

  • \(N+Ctr+FE\) , eli 0x4AFE

  • \(N+Ctr+FF\) , eli 0x4AFF

Jos vielä lisäisimme laskuriin vielä yhden arvon, se saisi uudestaan arvon 0x00. Tällaista tilannetta ei saa syntyä! Varsinaisen lohkosalaimen ulkopuolella on pidettävä huoli, että jos laskuri alkaa lähestymään suurinta arvoaan, on neuvoteltava uusi kertakäyttöluku. Näitä tilanteita varten on olemassa erilaisia salaukseen liittyviä neuvotteluprotokollia, mutta emme käy niitä läpi tällä kurssilla.

Edellisen yksinkertaisen laskurin lisäksi törmäät varmasti muihinkin laskurikäsitteisiin. Esimerkiksi Galois-laskuri on nimestään huolimatta paljon muutakin kuin vain laskuri. Aiheeseen kannattaa ajan salliessa perehtyä itsenäisesti.

Vastaa edellisten selitysten perusteella seuraaviin väittämiin.

Valitse oikeat vaihtoehdot.

Valitse oikea vaihtoehto.

Laskurimoodin visualisoiminen

Voimme tehdä lohkosalaimesta jonosalaimen siten, että kertakäyttöluvusta ja laskurista tuotetaan avaimella salaamalla bittikuvio, joka toimii seuraavaksi käytettynä avaimena. Tämä tapahtuu seuraavan kuvan osoittamalla tavalla.

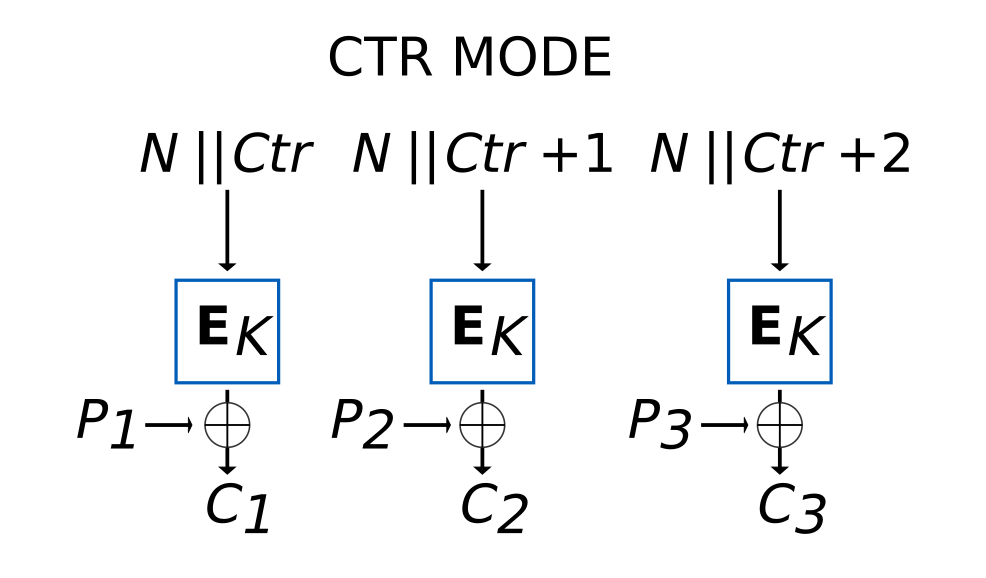
../_images/l5_ctr_mode.png

  • Lohkosalain käyttää avainta \(K\).

  • Lohkosalain muodostaa sisään tulevasta datasta avainketjua \(KC_i\).

  • Lohkosalaimelle tuleva data on kertakäyttöluvun (engl. NONCE) \(N\) ja laskurin \(CTR\) yhdistelmä \(N||CTR\).

  • Avainketjun symboleja ei ole piirretty kuvaan, mutta ne siis ovat lohkosalaimen tuottamia bittikuvioita.

  • Kertakäyttöluku \(N\) säilyy samana yhden viestikokonaisuuden ajan. Esimerkiksi yhden podcastin tai striimin ajan. Sen voi myös vaihtaa tai joutua vaihtamaan jonkun ennalta määrätyn salausten lukumäärän jälkeen.

  • Selväkielen salattava viesti \(P_i\) voi sisältää mielivaltaisen määrän bittejä aina lohkon kokoon eli 128 bittiin asti.

  • Salattavan datan \(P_i\) ei tarvitse olla lohkon kokoinen!

  • Laskuri \(CTR\) voi olla yksinkertainen laskien 0, 1, 2, … N tai edistyneempi.

  • Laskuri ei saa saada yhdellä kertakäyttöluvulla samaa arvoa kahdesti.

  • Tuotettu avainketjun lohko \(KC_i\) prosessoi selväkielen bittikuvioita \(P_i\) käyttämällä XOR-funktiota.

  • Näin tuotetaan avainketjua saapuvista data-alkioista \(P_1\) … \(P_M\) lasketaan XOR-funktiolla salakieltä \(C_1\) … \(C_M\).

  • Salatut lohkot tai bitit voi lähettää heti eteenpäin ja vastaanottaja pystyy purkamaan salaltut bitit välittömästi.

Kun salattu tieto on siirretty vastaanottajalle, vastaanottaja voi heti dekoodata saapuneen paketin ja käyttää selväkielistä lohkoa esimerkiksi omassa video-, audio- tai pelisovelluksessaan.

AES-jonosalauksen purku on kuvattu seuraavassa kuvassa. Huomaa, että se on aivan sama kuin enkoodaus. Ainoastaan \(C_i\) ja \(P_i\) vaihtavat paikkaa keskenään.

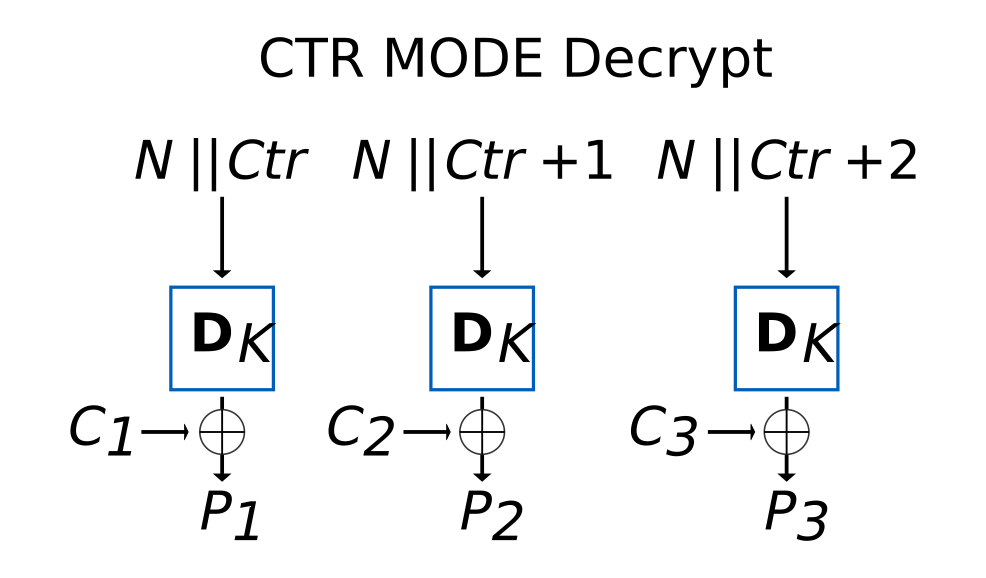
../_images/l5_ctr_mode_decrypt.png

  • AES-lohkosalain tuottaa purkuun tarvittavan avainketjun annetun kertakäyttöluvun ja saapuvan lohkon järjestyksen perusteella.

  • Laskurin arvoa ei saa käyttää kahdesti saman kertakäyttöluvun kanssa.

  • Purettua dataa voi käyttää välittömästi välittömästi ensimmäisen dekoodatun lohkon \(P_1\) laskemisen jälkeen.

Vastaa edellisten selitysten perusteella seuraaviin väittämiin.

Valitse oikeat vaihtoehdot.

Valitse oikea vaihtoehto.

Esimerkki salauksesta AES-salaimella CTR-moodissa

Tarkastellaan esimerkkiä, jossa salaamme viestin KAHVI Charlotassa on hyvää ja vahvaa!. Suoritamme salauksen ensin yksi merkki kerrallaan ja tämän jälkeen viesti salataan oikealla AES-jonosalaimella.

Seuraava koodisolu on yksinkertaistettu versio Python-kirjaston esimerkeistä. Luodaan enkoodaus ja dekoodaus käyttäen perinteistä laskuria. Kertakäyttöluku voisi olla myös heikko satunnainen luku, joka muodostetaan esimerkiksi kellonajasta ja päivämäärästä. Tässä esimerkissä käytämme kuitenkin aitoja entropia-altaasta ammennettuja satunnaislukuja.

Inactive
from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, modes
import os

def ctr_enkoodaus(avain, viesti):
    # Arvotaan kertakäyttönumero satunnaisuudesta
    # Eli alustetaan N satunnaisella 128-bittisellä luvulla
    N = os.urandom(16)

    # Tehdään enkoodaaja avaimesta ja laskurista
    enkryptaaja = Cipher(algorithms.AES(avain),modes.CTR(N),).encryptor()

    # Suoritetaan salaus
    salattu = enkryptaaja.update(viesti) + enkryptaaja.finalize()

    return (N, salattu)

def ctr_dekoodaus(avain, N, salateksti):
    # Tehdään dekoodaaja, avaimesta ja laskurista
    dekoodaaja = Cipher(algorithms.AES(avain), modes.CTR(N),).decryptor()

    return dekoodaaja.update(salateksti) + dekoodaaja.finalize()

suuri_luku = b"S\xef8\x8e\xc8\xddff\xf4\x81\xc7 '2\x97\x88\x86\t3\x12\xfbTI5FQ\x05$P\xe85o\\a\xae\x80i=U\x16\t3\xc0i\xbd\xee\xcd\xc0\\\xf6\x13\x0f\xe8jK\x0e\xd9\xf8\xab\xbc\r!0d?\nv\xad\x06\x83\x01,\x83\xf9%\xa8n4\x12\xb3gU\x12\xda\xecw!\xf2O\xb5\r\x1e\xdd\xf0\xa2H5\xe9\xf2\x81\xd4B\x91\xf7r\xfaI!d\xf7\xfa\xafW\xce\xb2\x00x]\xb2[\xf5@:\x07\x9d\x9db\xca\xa8?Ue3G\xe1YVh\x80\x051g\x00\x07hQ\xc4\xf3K\x1b\x0f\\\x08\xfe\x19&6\xb2\x14\xcb\x90\xfd\xfdq+\xd6X\xa5\xc6Q\x84`U\x13\xee#Y\xb2\xdf8\x7fJ8l\x8bV\x89>\xe9\xc7\x83/\xdf\xf7(\x8b\xc0\xb3\xf8\xe11\x04\xcb\x99\x96[\xbdN\x8d\x8d-\xaa\x03\x90*m\xc3\xa1\x08\x91\x17\xd96^9#iX\xfc\xef \xdd\xd1\xcd\xff\xedY\x98\xbaA\xf2g\xbf\xb7q\xb4^\xa5\xc8\xd4\xcb\xd9\x0eZb\xf8"

avain = suuri_luku[:16]

print("Avain ja salaimen luotu")

Suoritamme salauksen enkoodauksen ja dekoodauksen merkeittäin alla olevien kuvien mukaisesti.

Salaus eli enkoodaus:

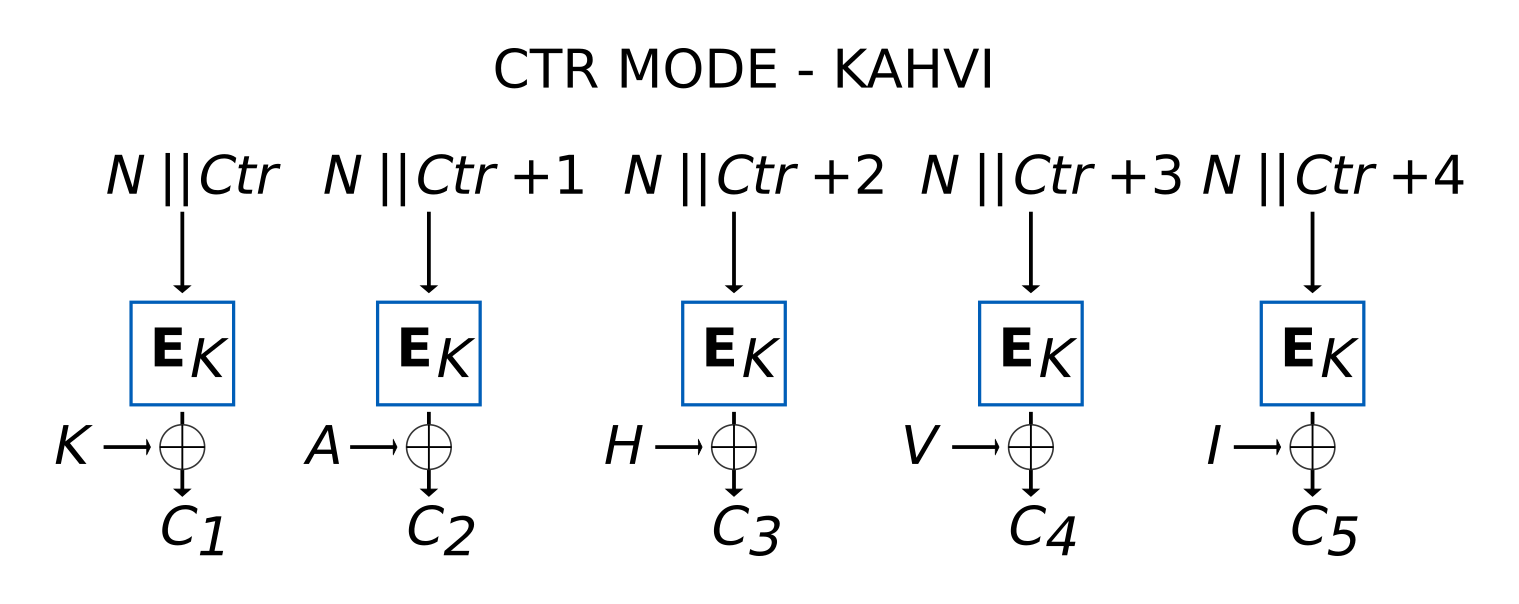
../_images/l5_ctr_mode_kahvi.png

Purku eli dekoodaus:

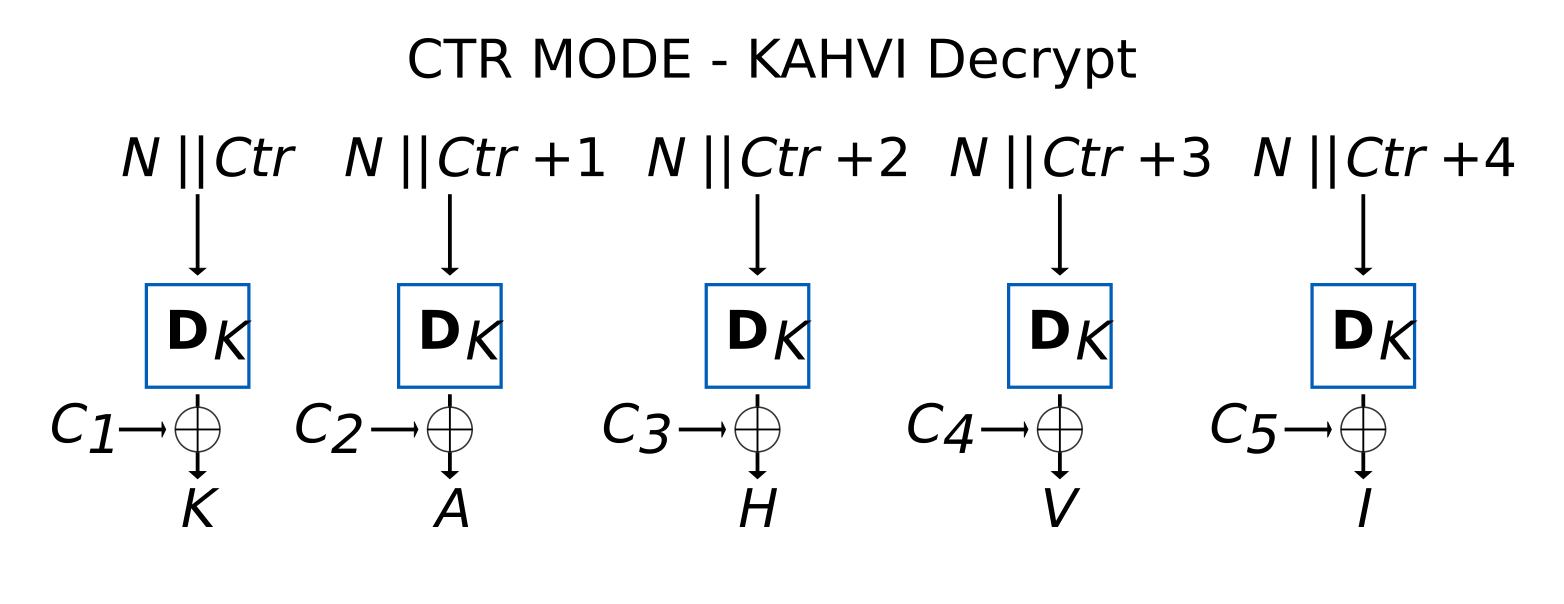
../_images/l5_ctr_mode_kahvi_decrypt.png

Kokeillaan salausta käytännössä. Ensimmäinen koodi salaa viestiämme yksi merkki kerrallaan. Tällöin luomme jokaiselle salattavalle kirjaimelle uuden kertakäyttöluvun.

Tämä on tuhlaava tapa käyttää arvokkaita aitoja satunnaislukuja.

Inactive
from xip import alusta_t630

avain, ctr_enkoodaus, ctr_dekoodaus = alusta_t630()

# Luodaan viesti
viesti ="KAHVI Charlotassa on hyvää ja vahvaa!".encode()

# Lähetetään kolme ensimmäistä merkkiä salattavaksi ja puretaan ne heti.
# Näemme myös joka kerralla käytetyt kertakäyttönumerot heksana.
for i in range(5):
    merkki = viesti[i:i+1]
    N, salateksti = ctr_enkoodaus(avain, merkki)

    print("\nKertakäyttöluku N on:", N.hex())
    print("Salattava merkki          on :", merkki.decode())
    print("Salattava merkki heksana  on :", merkki.hex())
    print("Salattuna merkki on heksana  :", salateksti.hex())

    print("Purettuna salattu merkki on  :", ctr_dekoodaus(avain, N, salateksti).decode())

Vastaa edellisten tekstien ja koodien perusteella seuraaviin väittämiin.

Valitse oikeat vaihtoehdot.

Valitse oikea vaihtoehto.

Tehokkaampi tapa on käyttää yhtä kertakäyttölukua yhdelle asiakokonaisuudelle, esimerkiksi yhdelle kuvalle, striimille tai videotiedostolle.

Inactive
from xip import alusta_t630

avain, ctr_enkoodaus, ctr_dekoodaus = alusta_t630()

# Luodaan viesti
viesti ="KAHVI Charlotassa on hyvää ja vahvaa!".encode()

# Salataan kerralla koko viesti salaimella
N, salateksti = ctr_enkoodaus(avain, viesti)
print("Kertakäyttöluku N on:", N.hex())
print("Saimme salatekstin  :", salateksti.hex())

# Puretaan viesti
print("Purettu viesti on   :", ctr_dekoodaus(avain, N, salateksti).decode())

Voimme siis salata viestin joko tavu kerrallaan tai yhdellä kerralla useamman tavun. Jonosalain sallii vaihtuvamittaisen tiedon enkoodauksen ja dekoodauksen.

Yhteenveto

Nyt ymmärrämme, että AES-salaimella voi toteuttaa jonosalaimen käyttämällä sitä CTR-moodissa.

Ymmärrämme myös sen, että salain tuottaa vaihtuvan mittaista tietoa, joka on saman mittaista kuin salattava tai purettava tieto.

Ymmärrämme nyt symmetristen salaimien perusperiaatteet, substituutio-permutaatio-verkon toiminnan ja miten lohkosalaimet ja jonosalaimet toimivat. Tähän mennessä olemme käyttäneet oppimiamme asioita vain yhteen kryptografian tavoitteeseen eli tiedon luottamuksellisuuden varmistamiseen.

Seuraavat oppimismoduulit avaavat oven tiedon autenttisuuden ja eheyden varmistamiselle. Jotta ne voidaan saavuttaa, opimme seuraavaksi mikä on tiivistefunktio ja mihin sitä käytetään.

Palautusta lähetetään...