Kryptoanalyysi - Frekvenssianalyysi¶
Analysoimme frekvenssianalyysillä tekstijonomuodossa olevia selvä- ja salatekstejä. Salaustekniikoiden kehittyessä myös niiden murtamisessa käytetyt tekniikat luonnollisesti kehittyvät. Tutkimusta salaustekniikoiden turvallisuudesta ja erilaisten murtamismenetelmien kehittämistä kutsutaan kryptoanalyysiksi.
Kryptoanalyysin katsotaan yleensä alkaneen 800-luvulla, kun arabialainen oppinut nimeltä Al-Kindi havaitsi, että eri kirjainten esiintymistiheys vaihtelee eri kielissä. Al-Kindi keksi, että tätä havaintoa voi hyödyntää salakirjoitusten purkamiseen.
Esimerkiksi suomen kirjakielessä aakkosten esiintymistodennäköisyys noudattaa seuraavaa jakaumaa:
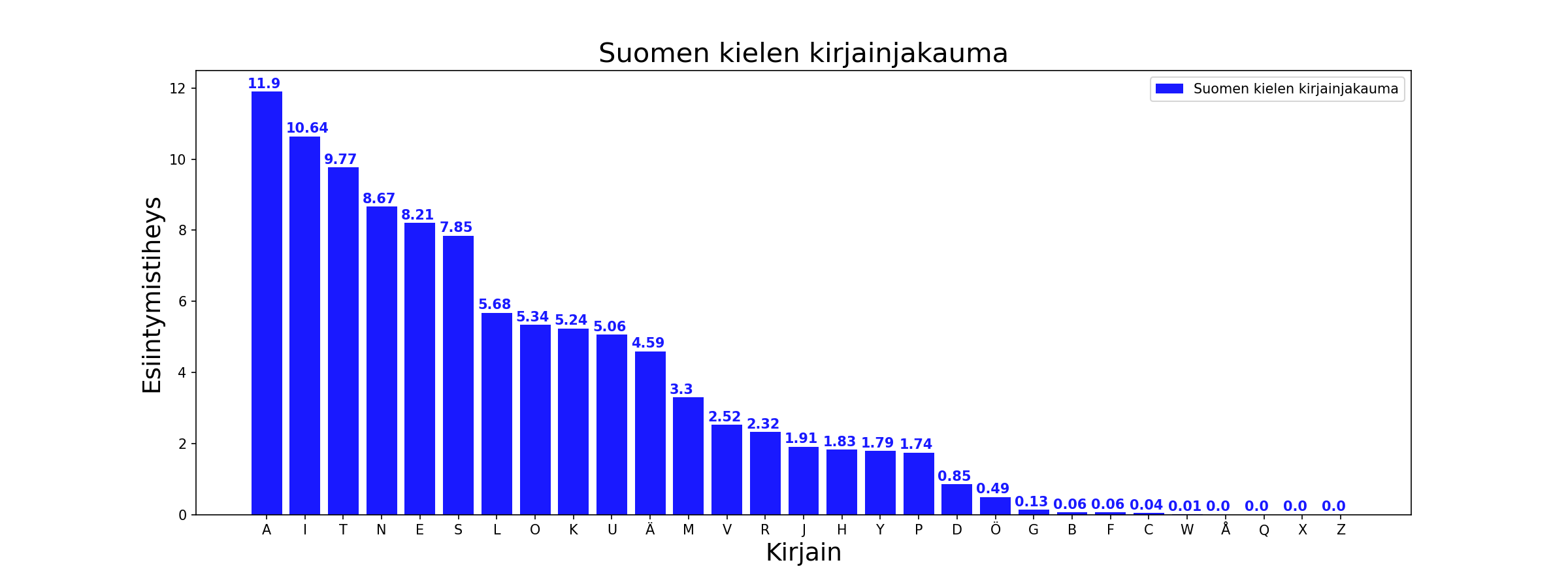
Lähde: Matti Pääkkönen, ”A: sta ö:hön Suomen yleiskielen kirjaintilastoja”¶
Suomenkielisessä tekstissä siis kirjaimet esiintyvät siten, että yleisin kirjain on ’A’ sitten ’I’ ja ’T’,’N’,’E’,’S’,’L’,’O’,’K’,’U’,’Ä’, jne. Tätä tietoa voi hyödyntää korvaussalaimella salattujen salakirjoitusten purkamisessa koska voidaan olettaa, että salakirjoituksessa yleisimmin esiintyvä kirjain on luultavimmin ’A’, seuraavaksi yleisin ’I’, jne.
Yksittäisen viestin todellinen jakauma ei luonnollisestikaan noudata yllä olevaa jakaumaa täsmällisesti, etenkään lyhyissä viesteissä. Siksi voi hyvin käydä niin, että kirjainten järjestys muuttuu hieman, eikä mekaanisesti purettu viesti ole ymmärrettävä. Etenkin matalimmilla esiintymistodennäköisyyksillä olevat kirjaimet usein vaihtavat paikkoja. Viestin aiheella on luonnollisesti suuri vaikutus eri kirjainten esiintymistiheyteen. Etenkin vieraskieliset erisnimet saattavat sotkea jakaumaa merkittävästi, vaikka viesti muuten olisi suomenkielinen. On silti varsin epätodennäköistä, että tavallisessa tekstissä jakauma poikkeaisi suuresti keskimääräisestä jakaumasta. Samoin on epätodennäköistä, että esim. ’Ö’ olisi viestin yleisin kirjain, mutta ’I’ toki voi useinkin olla.
Frekvenssianalyysi on siis erinomainen työkalu korvaussalainten murtamisessa.
Tutustuminen frekvenssianalyysiin¶
Seuraava koodisolu tuottaa suomen kielen kirjainjakauman histogrammina. Histogrammissa x-akselilla on kirjain ja y-akselilla kirjaimen esiintymismäärä vertailuaineistossa.
Näytetään suomen kielen kirjainjakauma.
from xip import näytä_kirjainjakauma
# Näytetään suomen kielen kirjainjakauman histogrammi.
näytä_kirjainjakauma()
Histogrammikuvasta nähdään, että A-kirjain on yleisin, I-kirjain toiseksi yleisin ja Å-, Q-, X-, Z-kirjaimet ovat harvinaisimpia. Histogrammin perustana oleva kirjainjakauma on alun perin julkaistu Kotimaisten kielten keskuksen Kielikello-lehdessä vuonna 1991. Pythonissa käyttämäämme kirjastoon kirjainjaukama on poimittu tältä verkkosivulta. On kuitenkin huomioitava, että suomen kieli kehittyy jatkuvasti, eikä tämä 30 vuotta vanhaan aineistoon perustuva jakauma enää välttämättä vastaa tämän päivän tilannetta.
Kurssiympäristöön on tuotu tälle sivulle useita tekstitiedostoja, joita voit analysoida. Alla oleva koodi näyttää saatavilla olevat tekstit. Tekstin kohdistaminen histogrammeihin ja salauksiin tapahtuu tekstin indeksinumerolla.
from xip import näytä_tekstit
näytä_tekstit()
Mukana ovat äidinkielen ylioppilaskokeen materiaalit keväältä 2021 indekseillä 10 & 11. Loput tekstit ovat kansanedustajien tekemiä kirjallisia kysymyksiä.
Frekvenssianalyysi kevään 2021 ylioppilaskokeiden teksteistä¶
Seuraavaksi katsomme aitoja tekstejä ja vertaamme niiden kirjainjakaumaa 30 vuotta vanhaan Kielikellossa julkaistuun kirjainjakaumaan.
Tarkastellaan ensimmäistä, kevään 2021 ylioppilaskokeessa ollutta tekstiä. Opettelemme harjoituksen kautta tulkitsemaan koodin tuottamaa tietoa samaan tapaan, jolla kryptoanalyytikot voisivat analysoida tekstejä.
Ensimmäiseksi tulostuu tekstin merkkimäärä. Jos merkkimäärä on kovin pieni, kirjainjakauma voi olla erittäin vääristynyt.
Toiseksi tulostuu tekstistä löytyneiden merkkien määrä.
Kolmanneksi tulostuu tekstistä puuttuneet suomalaiset aakkoset.
Seuraavaksi tuotetaan kuvaaja, joka näyttää annetun tekstin kirjainjakauman verrattuna oletettuun suomen kirjainten yleisyyteen. Huomaa, että kirjainten järjestys on sama kuin oletetussa kirjainjärjestyksessä. Palkit voivat näkyä eri väreillä, mutta palkkien värikoodit on kerrottu kuvaajan oikeassa yläkulmassa.
Kuvaajassa on esiintymistiheys myös numeroarvona.
Lopuksi tulostetaan virheyksikkönä, kuinka paljon näyte poikkeaa suomen kielen oletetusta kirjainjakaumasta.
Virheyksikkö on laskettu siten, että kunkin kirjaimen esiintymistiheyttä on verrattu oletettuun suomen kielen kirjainjakaumaan. Varsinainen virhe on laskettu kirjain kirjaimelta (odotustiheys - näytetiheys)^2 . Virheyksikkö on saatu laskemalla yhteen kaikkien kirjaimen ”neliöllinen virhe-etäisyys”. Eli siis \(\sum_{\text{merkki}=a}^{\text{merkki}=ö} (\text{näytetiheys}(\text{merkki})-\text{oletustiheys}(\text{merkki}))^{2} = \text{virhe}\)
from xip import freq_analyze
# Analysoidaan suomen äidinkielen YO-kokeen materiaali indeksillä 10
freq_analyze(10)
from xip import freq_analyze
# Analysoidaan suomen äidinkielen YO-kokeen materiaali indeksillä 11
freq_analyze(11)
Kuten kahdesta edellisestä esimerkistä nähdään, eivät myöskään ylioppilaskokeen aineistot noudata oletettua suomenkielen kirjainjakaumaa. Katsotaan seuraavaksi esimerkki, miten sama informaatio suomeksi ja ruotsiksi näkyy histogrammeissa.
Suomen ja ruotsin kielen ero frekvenssianalyysissä¶
Seuraavaksi analysoidaan kansanedustajan kirjallista kysymystä - ensin suomeksi ja sitten ruotsiksi. Esimerkki näyttää miten voimme tunnistaa, että kyseessä on suomen kielestä poikkeava kieli näkemättä itse tekstiä.
Frekvenssianalyysi Mats Löfströmin suomenkielisestä kirjallisesta kysymyksestä¶
Analysoimme esimerkeissämme tarkemmin kansanedustaja Mats Löfströmin esittämää kirjallista kysymystä. Hänen esittämä kirjallinen kysymys on valittu esimerkiksemme, koska sama sisältö on saatavilla sekä suomeksi (indeksillä 4) että ruotsiksi (indeksillä 5).
Katsotaan, kuinka hyvin Matsin suomenkielinen versio kirjallisesta kysymyksestä noudattaa olettamaamme suomen kielen kirjainjakaumaa.
from xip import freq_analyze
# Analysoidaan suomen kielinen kirjallinen kysymys.
freq_analyze(4)
Yllä olevasta frekvenssihistogrammista sekä tulostuneista tiedoista näemme seuraavat asiat:
Kirjallisessa kysymyksessä on 2858 merkkiä. Jos aineisto olisi lyhyt, se todennäköisesti ei noudattaisi suomen kielen kirjainjakaumaa.
Tekstistä puuttuvat aakkoset Q, W, Z, C, X, B, Å.
Kuvan alta näemme, että kirjoitus poikkeaa 8.24 virheyksikön verran suomen kielen oletetusta kirjainjakaumasta.
U- ja M-kirjaimet ovat yliedustettuna oletettuun kirjainjakaumaan verrattuna.
Ö- ja O-kirjaimet ovat aliedustettuna oletettuun kirjainjakaumaan verrattuna.
Edellinen teksti vastaa hyvin suomen kielen oletettua kirjainjakaumaa. Jos vertaat Mats Löfströmin esittämää välikysymystä esimerkiksi äidinkielen ylioppilaskokeeseen, on hänen teksti lähempänä suomen kirjaimien oletettua jakaumaa kuin ylioppilaskokeiden aineisto.
Frekvenssianalyysi Mats Löfströmin ruotsinkielisestä kirjallisesta kysymyksestä¶
Seuraava solu tuottaa frekvenssianalyysin kansanedustajan ruotsiksi esittämälle kirjalliselle kysymykselle. Aja koodi ja vastaa alla olevaan tehtävään.
from xip import freq_analyze
# Analysoidaan kirjallinen kysymys ruotsiksi.
freq_analyze(5)
Miten Carol voi hyödyntää frekvenssianalyysiä?¶
Kuvitellaan tilanne, jossa Carol löytää salakirjoituksen ja tietää, että Alice ja Bob käyttävät viestinnässään suomen kieltä ja korvaussalainta. Tässä esimerkissä Carol käyttää yleisesti tunnettuja salauksen analysointi- ja purkumenetelmiä (hän tietenkin osaa nämä menetelmät, koska hän on opiskellut Johdanto Kryptografian -kurssin). Carol käyttää tietokonetta selvittääkseen salakirjoituksen.
Salakirjoitus on seuraava:
Carol laskee viestin kirjaimien jakaumat seuraavalla koodilla:
from xip import tuota_frekvenssit
import pprint
# Alicen viesti Bobille
salakirjoitus="PFQÄFÄFDCLCSSTGSEFJQJJLNSJCSNSTDMMEQHSHHMVXTESHSD\
CSSPSTDQHHSHLEPSHSHHMÅSVXTNSEPSDCQQJSVCMQDQDSSRLDDSSTDLJJ\
SQDLTPQTXLVRFCCSQDQTLCCXÅMVJSÖQRLCXXTHFJPLTNQQHFTÖXXDCXJS\
MSTCSQSSPMTSPQCXPQLJCXDQTXFJLCCLENLQDQTSJQGL"
print("Viesti tallennettu muuttujaan: salakirjoitus")
kirjainten_määrät = tuota_frekvenssit(salakirjoitus)
print("Kirjainten määrä on:")
pprint.pprint(kirjainten_määrät)
Viestin yleisimmät kirjaimet ovat seuraavat: S (33), Q (22), C (17), T (16), D (15), L (15), J (13), jne.
Carol vertaa salakirjoituksen jakaumaa suomen kielen kirjainjakaumaan ja olettaa, että oikea korvaus viestin purkamiseksi olisi seuraava:
S => A, Q => I, C => T, T => N, L => E, D => S, J => L
D ja L kirjaimet voisivat yhtä hyvin olla toisinkin päin, koska molempia on salakielessä 15 kappaletta. Tällä korvauksella Carol saa:
–I—-STETAAN-A–LILLE-ALTA-ANS—I-A—–N-A-ASTAA-ANSI–A-E–A-A—-A–N-A–ASTIILA-T-ISISAA-ESSAANSELLAISEN-IN-E—TTAISINETT—-LA-I-ET–N–L-EN-II–N—ST-LA-ANTAIAA–NA-IT–IELT-SIN–LETTE–EISINALI-E
Carol visualisoi numeerisen datan seuraavalla koodilla:
from xip import laske_frekvenssit, näytä_kirjainjakauma, alusta_t421
salakirjoitus = alusta_t421()
# Carol vertaa salakirjoituksen frekvenssiä suomen kielen frekvenssiin.
frekvenssi_kirjaimet, frekvenssi_prosentit = laske_frekvenssit(salakirjoitus)
näytä_kirjainjakauma(frekvenssi_kirjaimet, frekvenssi_prosentit, "Alicelta Bobille", vain_aineisto=True)
näytä_kirjainjakauma()
Salakirjoitus on lyhyt, eikä se edusta selväkielenä suomen kielen jakaumaa täydellisesti. Tietokone auttaa Carolia korvausten selvittämisessä, mutta osa kryptoanalyysistä jää Carolin itsensä tehtäväksi.
Nykyisin salakirjoitusten purkamista helpottaa se, että viestien alussa tai lopussa on usein jokin samanlaisena toistuva vakioteksti. Carol arvaa Alicen aloittavan viestin sanoilla ”Moi Bob” ja lopettaa sen ”Terveisin Alice”. Tästä hän saa heti korvaukset:
P => M, F => O, Ä => B, E => R, N => V, G => C
Samalla Carol saa purettua viestiä lisää:
MOIBOBOSTETAANCAROLILLEVALTAVANS–RI-A—–NRA-ASTAAMANSI–A-ERMA-A—-A–NVARMASTIILA-T-ISISAA-ESSAANSELLAISENMIN-E–OTTAISINETT—-LA-I-ET–N-OLMENVII-ON—ST-LA-ANTAIAAM-NAMIT-MIELT-SIN-OLETTERVEISINALICE
Tästä tekstistä, sekä omasta mieltymyksestään mansikkakermakakkuihin, Carol saakin jo purettua viestin:
Murrettu viesti on:
Alicen ja Bobin järjestämä yllätys siis selviäisi Carolille helposti, koska Alice ja Bob käyttivät heikkoa salausta, joka on osattu murtaa jo yli tuhannen vuoden ajan!
Yhteenveto¶
Nyt ymmärrämme, miten frekvenssianalyysillä voi tuottaa luonnollisen kielen kirjainjakaumat. Absoluuttiset kirjainmäärät eivät ole kovinkaan kiinnostavia, vaan meitä hyödyttää kirjainten suhteellinen jakauma. Aiemmin mainittiin, että hyvä salain tuottaa enkryptauksessa salatekstiä, joka muistuttaa satunnaista kohinaa. Mitä tämä tarkoittaa frekvenssianalyysissä, kun käsiteltävä tieto on tekstiä??
Alla oleva kuva esittää hyvän tasaista jakaumaa tuottavan salaimen tuottaman salakielen kirjainjakauman. Tällöin salakielessä esiintyy jokaista merkkiä yhtä paljon. Kuvan kaltaista informaatiota analysoidessamme emme pysty päättelemään mitään salaimen, avaimen tai selvätekstin ominaisuuksista. On toivottavaa, että tekstitietoa käsittelevät salaimet tuottaisivat alla olevan kuvan mukaista salakieltä.
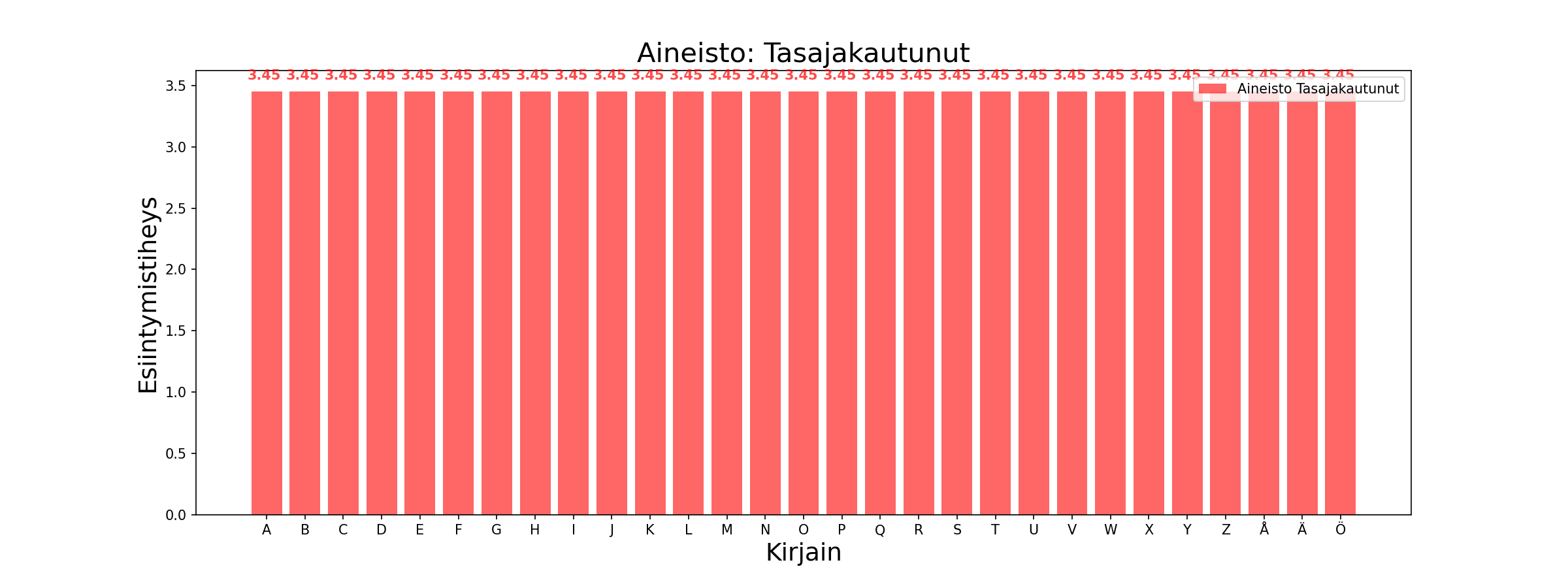
Nyt käyttämämme frekvenssianalyysi ei kata kaikkia mahdollisia tietokoneen sallimia merkkejä tai bittikuvioita. Seuraavassa osiossa tulkitsemme datan jakaumaa klassisilla salaimilla näitä samoja tekstejä hyödyntäen. Periaate on sama, mutta tulevaisuudessa laskemme kuinka montaa eri bittikuviota, tavua tai sanaa esiintyy, sekä mikä niiden frekvenssi on.