Suuret luvut

Kurssilla on toistaiseksi käytetty lähes yksinomaan ”pienehköjä ”numeroita ja lukuja. Suurempiin lukuihin on aikaisemmin vain viitattu.

Pienehköt luvut ja turvataso

”Pienehkö” luku on esimerkiksi 128-bittinen luku. Olemme käyttäneet 128-bittistä lukua muun muassa avaimena. 128-bittinen avain voidaan esittää lukuna, jossa on 39-numeroa. Esimerkiksi 128-bittisen 39-numeroisen luvun 215826290122223003264819486280856312625 binääriesitys on

0b10100010010111101010000110101001100010100111101111100011110110011110001111010010010100010001101011000110101111110001101100110001

Käsittelimme jo aiemmin turvatasoa. Turvataso määrittää todennäköisyyden, että raa’alla voimalla tapahtuva laskenta riittää murtamaan salaimen.

Olemme tähän mennessä käyttäneet symmetrisiä salaimia, jossa 128-bittinen avain tuottaa 128-bittisen turvatason.

Kun katsot edellistä 128-bittistä bittijonoa, se voi auttaa hahmottamaan, mitä 128-bittisellä turvallisuudella tarkoitetaan:

• Hyökkääjän pitää kokeilla kaikkia avainvaihtoehtoja murtaakseen salaimen.

• 128 bitin tapauksessa tilanne on sama, kuin jos kokeilisi mikä luku numeroiden 0 ja \(2^{128}-1\) (eli 340282366920938463463374607431768211455) välillä on oikea avain.

Symmetrisissä salaimissa avaimen koon kasvattaminen 128 bitistä ja 129 bittiin kaksinkertaistaa kokeiltavan avainavaruuden koon. Tällöin avainavaruuden koko on \(2^{129}\) ja suurin sillä saatava luku on 680564733841876926926749214863536422911. Samalla tuplaamme avaimen murtamiseen tarvittavan ajan tai raa’alla voimalla tapahtuvaan laskentaan vaadittavan laskentakapasiteetin.

Laskimme jo aiemmin, että tällaisissa tapauksissa suurellakin laskentakapasiteetilla vie valtavasti aikaa kokeilla kaikki mahdolliset avaimet.

---

Suurten lukujen hahmottaminen

Suuria lukuja on todella vaikea hahmottaa. Edellisessä kappaleessa 128-bittinen luku esitellään ”pienehkönä”. Mikä on sitten suurehko luku ja mihin se vertautuu?

Esimerkkinä suuresta luvusta voidaan mainita se, että atomien määrän maapallossa on arvioitu olevan noin \(1.3 \cdot 10^{50}\) eli noin \(2^{167}\) kappaletta. Tämä tarkoittaa siis sitä, että jos salaimessa käytettäisiin 167-bittisiä avaimia, silloin oikean avaimen löytäminen olisi verrattavissa tietyn atomin löytämiseen maapallosta satunnaisesti kokeilemalla! Nykyään usein käytetään avaimia, joiden turvataso on 256 bittiä. Symmetrisissä salaimissa tällainen turvataso vastaa 256-bittistä avainta. Näin ollen avainvaihtoehtojen määrä on vielä huomattavasti suurempi.

Julkisen avaimen järjestelmissä käytettävät luvut ovat usein vielä huomattavasti edellä mainittuja lukuja suurempia. Joudumme käyttämään suurempia lukuja saavuttaaksemme tietyn turvatason. Esimerkiksi, jotta myöhemmin esiteltävän RSA-järjestelmän tapauksessa saavutettaisiin 128-bittinen turvataso, on käytettävä 3072-bittisiä lukuja. Julkisen avaimen järjestelmien tapauksessa avainten koko ja saavutettu turvataso eivät siis enää ole sama asia. Tyypillisesti julkisen avaimen järjestelmissä täytyy käyttää huomattavasti suurempia avaimia, kuin mikä niillä saavutettava turvataso on.

---

Kysymys 1

Ideaalinen symmetrinen salain käyttää 128-bittistä avainta, jolloin:

Avainten määrä on \(2^{128}-1\).

Saavutetaan 128-bittinen turvataso.

Kysymys 2

Valitse oikea vaihtoehto.

Avaimet ja tuvataso määritellään bitteinä.

Epäsymmetrisissä salaimissa avaimen koko on sama kuin turvataso.

Kysymys 3

RSA-menetelmässä voidaan käyttää eri avainpituuksia. Valitse oikea vaihtoehto.

Jos käytämme RSA:n kanssa 2048-bittistä avainta, turvataso on ainakin 128 bittiä.

Jos käytämme RSA:n kanssa 4096-bittistä avainta, turvataso on alle 128 bittiä.

Jos käytämme RSA:n kanssa 3072-bittistä avainta, turvataso on oletettavasti 128 bittiä.

---

---

Tekijöihin jako

RSA:n tapauksessa turvallisuus perustuu siihen, että suuria lukuja on erittäin vaikea jakaa tekijöihin. Etsimme siis niitä alkulukuja, joiden tulona jokin luku esiintyy.

Jos esimerkiksi otetaan luku 77, löytyvät sen alkulukutekijät 7 ja 11 välittömästi ilman apuvälineitä. Alkuluvuilla on tärkeä rooli lukuteoriassa. Samoin esimerkiksi 46127 on sekin vielä ratkaistavissa melko nopeasti: 193 ja 239. Ihmisen rajat jakaa lukuja tekijöihin tulevat vastaan melko pian lukujen kasvaessa. Tietokoneella lukujen jako tekijöihin voidaan suorittaa helpommin. Tietokoneidenkin rajat tulevat kuitenkin vastaan, kun käytetään riittävän suuria lukuja.

Tekijöihin jakoon on olemassa tehokkaampia menetelmiä kuin vain kaikkien vaihtoehtojen kokeileminen. Näiden menetelmien yksityiskohtainen tarkastelu ei kuulu enää tämän kurssin aihepiiriin, mutta lisätietoa löytyy esimerkiksi Wikipediasta. Tämän hetken parhaana algoritmina pidetään yleistä lukukuntaseulaa.

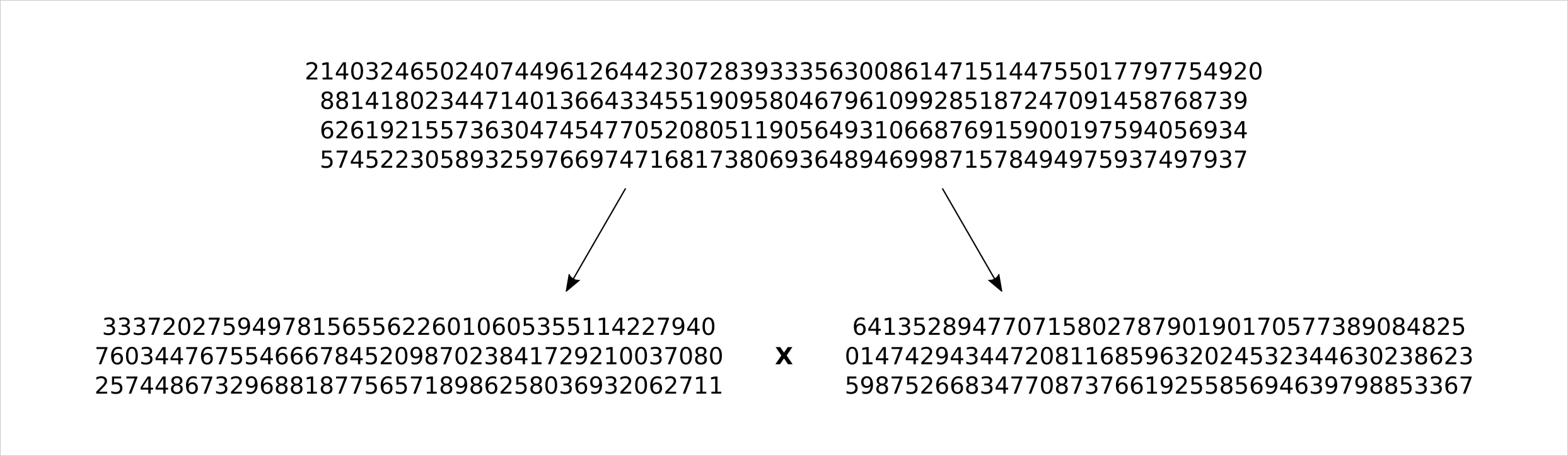
Oheisessa kuvassa näytetään esimerkki suuren numeron jakamisesta tekijöihin. Luku on 240-numeroinen (eli 795-bittinen) ja kului 900 vuotta laskenta-aikaa jakaa se tekijöihin. Laskenta suoritettiin useilla tietokoneilla rinnakkain, joten varsinaista kalenteriaikaa tekijöihinjakoon ei kulunut näin paljon. Luku jaettiin tekijöihin vuonna 2019.

Vuonna 2021 ennätys rikottiin jakamalla 250-numeroinen (eli 829-bittinen) luku tekijöihin. Tähän kului 2700 vuotta laskenta-aikaa.

---

Kysymys 1

Joudut ehkä käyttämään laskinta jossain vaiheessa. Valitse oikeat vaihtoehdot.

Luku 51 on alkulukujen 17 ja 3 tulo, eli \(51 = 17*3\).

Luku 6 on alkulukujen 3 ja 2 tulo.

Luku 101 on jaollinen luvulla 1.

Luku 10807 ei ole jaollinen luvulla 107.

Kysymys 2

Näissä joutunet käyttämään laskinta. Valitse oikeat vaihtoehdot.

Luvun 1185917 toinen tekijä on 1091.

Luvun 1185917 toinen tekijä on 1087.

Luvun 60587407 toinen tekijä on 7853.

Luvun 500555 yksi tekijä on 11, toinen 19 ja kolmas 479

---

---

Miten suurilla luvuilla lasketaan?

Kuten jo mainittiin, RSA:ssa käytetyt avaimet ovat vielä paljon suurempia lukuja. Pienin nykyään suositeltu koko on 2048 bittiä.

Esimerkiksi eräässä haasteessa (ns. RSA-2048 challenge), tehtävänä on jakaa tekijöihin seuraava luku:

251959084756578934940271832400483985714292821262040320277771378360436620207075955562640185258807844

069182906412495150821892985591491761845028084891200728449926873928072877767359714183472702618963750

149718246911650776133798590957000973304597488084284017974291006424586918171951187461215151726546322

822168699875491824224336372590851418654620435767984233871847744479207399342365848238242811981638150

106748104516603773060562016196762561338441436038339044149526344321901146575444541784240209246165157

233507787077498171257724679629263863563732899121548314381678998850404453640235273819513786365643912

12010397122822120720357

Koska käsiteltävät luvut ovat todella suuria, on niiden käsittely jo normaalissa tiedon salaamisessa ja purkamisessakin haastavaa. Tavallinen laskuoperaatio näissä järjestelmissä on potenssiin korotus ja modulo.

Seuraava yhtälö on yleinen esimerkki laskennasta, jossa luku \(x\) korotetaan potenssiin \(e\), jonka tuloksesta otetaan modulo \(n\) .

\(y = x^e \pmod{n}\),

RSA-menetelmässä lukujen \(e\), \(n\) ja \(x\) oletetaan olevan samaa suuruusluokkaa (esim. 3072 bitin kokoisia). Tämä lasku voidaan laskea tehokkaasti perättäisillä kertolaskuilla moduloon \(n\) . Tällöin vaadittava kertolaskujen määrä on korkeintaan kaksi kertaa eksponentin pituus bitteinä. Algoritmissa eksponentti esitetään ensin binääriesityksenä.

---

Laskentaesimerkki

Tehdään yksi esimerkkilaskenta pienillä luvuilla. Sama laskenta toimii myös suurilla luvuilla. Näytämme, miten seuraava laskenta toteutetaan algoritmisesti oikein.

Kuten matemaatikot aloittavat, olkoon:

• \(n=17\)

• \(x=3\)

• \(e=10\), jonka binääriesitys on 0b1010.

• Merkitään eksponentin bittimäärää \(t\):llä eli nyt \(t=4\).

• \(i\) saa arvoja \(i=0,\ldots,t-1\)

Algoritmissa lasketaan ensin \(x^{2^i}\) eli nyt lasketaan:

\[\begin{split}\begin{align*} x^{2^0} &= x = 3 \\ x^{2^1} &= x \cdot x = 9 \\ x^{2^2} &= x^2 \cdot x^2 = 81 \equiv 13 \pmod{17} \\ x^{2^3} &= x^4 \cdot x^4 = 169 \equiv 16 \pmod{17} \end{align*}\end{split}\]

Kongruenssi ilmaisi siis jakojäännösluokkan modulorenkaassa.

Tämän jälkeen kerrotaan yllä lasketut välitulokset \(x^{2^i}\):t keskenään, jos eksponentin \(e\) bitti \(i\) on ykkönen.

Muistetaan että tietokonemaailmassa järkevä indeksointi alkaa nollasta.

Eli tässä tapauksessa, kun eksponentin \(e\) bitit olivat 1010 lasketaan:

\(y = x^{2^1} \cdot x^{2^3} \pmod{17} = 9 \cdot 16 \pmod{17} = 144 \pmod{17} = 8\).

Näin pienen laskun voi laskea vielä tavallisella laskimella ja voitkin kokeilla, että laskimella todella saadaan sama tulos kuin yllä olevalla algoritmilla. Tavallisella laskimella ei kuitenkaan voi enää laskea laskuja, jotka tapahtuvat esim. 3072-bittisillä luvuilla!

Teemme alla saman laskennan Python-koodilla. Voit hyödyntää tätä koodisolua alla olevassa tehtävässä, jollet halua käyttää kynää ja paperia.

Inactive

Activate

import math

# Alustetaan muuttujat
n = 17
x = 3
e = 10

# Lasketaan e:stä seuraavat asiat
e_bitit = bin(e).split('b')[1]
e_pituus = len(e_bitit)

# Näytetään muuttujat
print("n = {}; x = {} ; e = {}".format(n, x, e))
print("e:n bittikuvio = {}, jolloin t = {}".format(e_bitit, e_pituus))
print("Tällöin i käy 0:sta {}:een".format(e_pituus-1))

# lasketaan x^2^i välitulokset talteen
välitulokset = []

for i in range(e_pituus):
    välitulokset.append(x**(2**i)%n)

print("Välitulokset ovat:", välitulokset)

# Suoritetaan laskenta loppuun, tarkistetaan e:n bitit ja lasketaan tulo.
print("eksponentin bitit:",e_bitit)

tulos = 1

# Vähiten merkitsevä bitti (LSB) on bittijonossa "oikealla".
# Tällöin oikeanpuoleisin e:n bitti on järjestysnumeroltaan "nolla".
# Käymme e:n bitit läpi oikealta vasemmalle.

for i, bitti in enumerate(reversed(e_bitit)):

  # Jos tarkasteltava bitti on 1, kerrotaan välitulos mukaan tulokseen mod(n)
  if bitti == '1':
      tulos = (välitulokset[i] * tulos)%n
  else:
      pass

print("Ja laskennan tulos on:", tulos)

---

Kaikki tehtävät on mahdollista tehdä kynällä ja paperilla. Voit halutessasi myös muokata edellistä koodisolua.

Kysymys 1

Jos 128-bittinen avain vaihdetaan 256-bittiseen avaimeen,

Avainvaihtoehtojen määrä kasvaa kaksinkertaiseksi, koska \(256/128 = 2\).

Avainvaihtoehtojen määrä kasvaa kahdeksankertaiseksi, koska 256:n kaksikantainen logaritmi on 8.

Avainvaihtoehtojen määrä kasvaa \(2^{128}\)-kertaiseksi, koska \(2^{256} / 2^{128} = 2^{128}\).

Avainvaihtoehtojen määrä kasvaa, mutta on mahdotonta sanoa, kuinka paljon.

Kysymys 2

Jos suoritat laskuoperaation \(y=x^e \pmod{n}\), niin että \(x=7\), \(e=15\) ja \(n=23\), niin

\(t=4\) ja eksponentin bitit ovat 0b1111.

\(t=3\) ja eksponentin bitit ovat 0b111.

\(t=4\) ja eksponentin bitit ovat 0b1110.

Kysymys 3

Jos suoritat laskuoperaation \(y=x^e \pmod{n}\), niin että \(x=7\), \(e=15\) ja \(n=23\), niin

\(y=12 \pmod{23}\).

\(y=13 \pmod{23}\).

\(y=14 \pmod{23}\).

---

---

Yhteenveto

Nyt ymmärrämme, mitä kryptografiassa tarkoitetaan suurilla luvuilla.

• Vaikka symmetristen salainten 128-bitin avaimia on paljon, ne ovat kuitenkin ”pienehköjä” lukuja verrattuna suuriin lukuihin.

• Epäsymmetrisissä menetelmissä avaimien pituudet voivat olla tuhansia bittejä.

• Epäsymmetrisissä menetelmissä turvataso ja avaimen pituus eivät ole enää sama asia.

• Osaamme käytännössä laskea potenssiinkorotukset modulorenkaan sisällä nopealla tavalla.

Seuraavaksi sovellamme juuri oppimiamme tietoja Diffie–Hellman-avaintenvaihtoprotokollan ja RSA-menetelmän kanssa.

Palautusta lähetetään...

×

Identtinen palautus

Tämä palautus on identtinen aikaisemman palautuksen kanssa. Oletko varma, että haluat lähettää palautuksen?

Peruuta Lähetä