Kurssin viimeisimmän version löydät täältä: Johdatus kryptografiaan: 2024
Tiivistefunktioiden ominaisuudet¶
Edellisessä osiossa havainnollistettiin, miten digitaalisesta datasta tuotetaan tiivistefunktion avulla tiiviste.
Katsotaan matematiikan näkökulmasta, miten haluamme tiivistefunktion toimivan:
Tiivistefunktio kuvaa lähtöjoukon maalijoukkoon. Tämä tarkoittaa sitä, että on olemassa funktio \(f\) , joka kuvaa lähtöjoukon \(X\) maalijoukkoon \(Y\).
Funktion toteuttama kuvaus on surjektiivinen, mutta ei injektiivinen. Tämä tarkoittaa sitä, että tiivistefunktiolle ei ole olemassa käänteisfunktiota \(f^{-1}\).
Lähtöjoukon kokoa ei ole rajoitettu. Käytännössä tämä tarkoittaa sitä, että lähtöjoukko voi olla pieni tai hyvin suuri. Esimerkiksi valtava tiedosto.
Maalijoukko on tarkkaan määritelty. Maalijoukko voi olla esimerkiksi 256-bittinen luku, jolloin maalijoukko on \(\{0, 1, \cdots , 2^{256}-1 \}\). Toisaalta on olemassa laajennetun ulostulon tiivistefunktoita, jotka pystyvät tuottamaan käytännössä rajoittamattoman kokoisen tiivisteen. Silti laskennassa maalijoukko on periaatteessa tarkkaan määritelty.
Hyvä tiivistefunktio on taipumaton (engl. non-malleable). Tämä tarkoittaa sitä, että pieni muutos lähtöjoukossa ei saa kuvautua pieneksi tai systemaattiseksi muutokseksi maalijoukossa.
Seuraavat tiivistefunktioiden toiminnallisuudet ovat mahdollisia silloin, kun tiivistefunktiolla on aiemmin kuvatut toivotut ominaisuudet:
Koska tiivistefunktio on surjektiivinen, on mahdollista, että tiivistefunktio tuottaa kahdelle lähtöjoukon alkiolle, eli alkukuvalle, saman maalijoukon tiivisteen. Tätä kutsutaan törmäykseksi (engl. collision).
Tiivisteestä ei käytännössä pysty laskemaan, mistä alkukuvasta (engl. pre-image) se on tuotettu.
Esimerkiksi ensimmäisen osion tiivistefunktiota selivttävässä kuvassa näkyy tiiviste
340e1bd57e10e955cb5c49a8a87da3dbe1e366bd140e86c4bd24e1902f1df357. Ei ole olemassa tapaa laskea mistä informaatiosta kyseinen tiiviste on tuotettu.
Tutkitaan tarkemmin joitain edellä mainittuja ominaisuuksia.
Tiivistefunktio¶
Vaikka tiivistefunktioita on käytetty tietokoneissa jo pitkään, niitä kehitetään edelleen tänäkin päivänä. Historiallisesti kattavin tarjonta on sellaisista tiivistefunktioista, jotka tuottavat suuresta alkukuvasta pienen tiivisteen (engl. compression function). Osa tiivistefunktioista hyödyntää lohkosalainta laskiessaan tiivistettä. Tällaisia ovat esimerkiksi SHA-1 ja SHA-2. Käytämme esimerkeissämme SHA-2-perheen SHA-256-algoritmia, joka tuottaa 256-bittisen tiivisteen.
Viime aikoina on kehitetty myös tiivistefunktioita, jotka perustuvat permutointiin ja yksinkertaiseen XOR-laskentaan. Niille ei ole vielä vakiintunut suomenkielistä nimeä. Englanniksi tällaisia funktioita kutsutaan nimellä sponge function. Suomeksi nimi voisi siis olla esimerkiksi sienifunktio. Tunnetuin tällainen tiivistefunktio on SHA-3 (Keccak).
Suuri osa uusimmista tiivistefunktioista pystyy tuottamaan vakiomittaisen tiivisteen lisäksi vapaamittaisen tiivisteen. Tällaisia laajennetun ulostulon tiivistefunktoista kutsutaan englanniksi nimellä extendable-output function (lyhenne XOF). Tällaista funktiota käyttämällä on mahdollista tuottaa samalla funktiolla tiiviste, jossa on vapaavalintainen määrä bittejä.
Lähtöjoukosta maalijoukko¶
Oletetaan, että meillä on SHA256-tiivistefunktiolla laskettu 256-bittinen tiiviste: 65c191580096072e9e31eb5e92b3cbca54aa5b47eb0251a2410167bc388f10d0 .
Tämän tiivisteen alkukuva on merkkijono (eli tässä tapauksessa virke): ”Joulupukki asuu Korvatunturilla.” Voit kokeilla, saatko saman tiivisteen käyttämällä annettuja koodiesimerkkejä.
Mahdollisia tiivisteitä on ”vain” \(2^{256}-1\) kappaletta.
Lähtöjoukon kokoa ei ole rajoitettu. Tämä tarkoittaa sitä, että meillä on olemassa ääretön määrä mahdollisia alkukuvia, joista syntyy sama tiiviste. Tätä tilannetta tarkastellaan tarkemmin kohdassa Tiivisteiden törmäys ja syntymäpäiväparadoksi.
Alkukuvien kuvautuminen¶
Haluamme, että tiivistefunktio kuvaa alkukuvia maalijoukkoon näennäisesti hyvin satunnaisesti.
Katsotaan esimerkkiä, jossa alkiot ovat ascii-merkit A, B ja C. Bitteinä merkit A, B, ja C eroavat toisistaan vain vähän:
A on bitteinä
0b1000001B on bitteinä
0b1000010C on bitteinä
0b1000011
Haluamme tavan tulkita kuinka paljon bittikuviot eroavat toistaan. Yksi tapa määrittää bittikuivoiden eroavaisuudet on laskea Hamming-etäisyys (engl. Hamming distance). Siinä laskemme, kuinka monta yhden bitin muutosta on tehtävä, jotta bittijonot ovat samat. Hamming-etäisyys kertoo, kuinka monen muutoksen takana, eli kuinka kaukana, kaksi bittijonoa ovat toisistaan.
Voimme nyt laskea edellisten kirjainten etäisyydet toisistaan Hamming-etäisyyksinä:
Merkkien A ja C välillä on yhden bitin ero, jolloin Hamming-etäisyys on 1.
Merkkien B ja C välillä on yhden bitin ero, jolloin Hamming-etäisyys on 1.
Merkkien A ja B välillä on kahden bitin ero, jolloin Hamming-etäisyys on 2.
Käytämme itse tehtyä kirjastoa, jota käytimme jo edellisessä osiossa. Funktio laskee annettujen tavujen (eli 8 bitin ryhmien) eron Hamming-etäisyytenä.
Funktio laske_tiiviste :
Laskee SHA256-tiivisteen.
Palauttaa joko merkkijonon (
tekstipalaute=True) tai tavuja (tekstipalaute=False).
Funktio testaa_tiivisteet laskee kahden bittijonon Hamming-etäisyyden.
Käytämme funktiota kahdella tapaa:
Laskemme alkukuvien Hamming-etäisyyden
Laskemme tiivisteiden Hamming-etäisyyden
Tuomme funktion käyttöön kurssin xip -kirjastosta.
# Otetaan käyttöön omat tiivistefunktiot, lähes samat kuin edellisellä sivulla.
from xip import laske_tiiviste, testaa_tiivisteet
# Muunnetaan ascii-merkki tavuksi eli 8-bitiksi
a = 'A'.encode()
b = 'B'.encode()
c = 'C'.encode()
# Näytetään ascii-merkit bitteinä
print("A bitteinä:", bin(int.from_bytes(a,'big')))
print("B bitteinä:", bin(int.from_bytes(b,'big')))
print("C bitteinä:", bin(int.from_bytes(c,'big')))
# 1. Lasketaan alkukuvien eli ASCII merkkien erot bitteinä (hamming-etäisyys):
print("A:n ja C:n ero on:",testaa_tiivisteet(a,c), "bitti(ä)")
print("B:n ja C:n ero on:",testaa_tiivisteet(b,c), "bitti(ä)")
print("A:n ja B:n ero on:",testaa_tiivisteet(a,b), "bitti(ä)")
# Lasketaan tiivisteet niin että ne voidaan tulostaa.
# Pyydetään funktiota palauttamaan tiivisteet heksadesimaali merkkijonona.
a_tiiviste_hex = laske_tiiviste("A", tekstipalaute=True)
b_tiiviste_hex = laske_tiiviste("B", tekstipalaute=True)
c_tiiviste_hex = laske_tiiviste("C", tekstipalaute=True)
print("A:n tiiviste on:", a_tiiviste_hex)
print("B:n tiiviste on:", b_tiiviste_hex)
print("C:n tiiviste on:", c_tiiviste_hex)
# 2. Lasketaan tiivisteiden hamming-etäisyydet a:n, b:n ja c:n välillä.
# Funktio palauttaa tiivisteen nyt tavu-muodossa, joka annetaan testaa_tiivisteet funktiolle
a_tiiviste = laske_tiiviste("A", tekstipalaute=False)
b_tiiviste = laske_tiiviste("B", tekstipalaute=False)
c_tiiviste = laske_tiiviste("C", tekstipalaute=False)
print("A:n ja C:n tiivisteissä eroa on", str(testaa_tiivisteet(a_tiiviste, c_tiiviste)), "bittiä")
print("B:n ja C:n tiivisteissä eroa on", str(testaa_tiivisteet(b_tiiviste, c_tiiviste)), "bittiä")
print("A:n ja B:n tiivisteissä eroa on", str(testaa_tiivisteet(a_tiiviste, b_tiiviste)), "bittiä")
Edellinen tehtävä näyttää, että vaikka ascii-merkkien alkukuvat ”A” ja ”B” eroavat vain yhdellä bitillä ascii-taulukossa, niistä lasketut tiivisteet eroavat hyvin paljon. Samoin alkukuvien ”B” ja ”C” välillä on yhden bitin ero, mutta tiivisteet eroavat huomattavasti.
Jos yritämme näiden tietojen pohjalta ennustaa, mikä olisi alkukuvan ”D” tiiviste, se on käytännössä mahdotonta. Tiivistefunktio kuitenkin pystyy laskemaan tuon alkukuvan tiivisteen nopeasti.
Tämän perusteella voimme tehdä johtopäätöksen, että SHA-256-tiivistefunktio vaikuttaa taipumattomalta. Alkukuvan muutosten ja tiivisteiden muutosten välillä ei näytä olevan selkeää yhteyttä. Lisäksi vaikuttaa siltä, että SHA-256-tiivistefunktion tuloksia ei ole mahdollista ennustaa muuten kuin laskemalla tiiviste.
Jos tiivistefunktio toimii hyvin, ei aiemmin lasketuista alkukuvista voi ennakoida jonkun toisen alkukuvan tiivistettä. Samoin jos tiivistefunktio toimii hyvin, täyttää se taipumattomuuden ehdot.
Tiivisteiden törmäys ja syntymäpäiväparadoksi¶
Jos kaksi tai useampi alkukuva tuottavat saman tiivisteen, sanotaan että on tapahtunut tiivisteiden törmäys. Oheinen kuva havainnollistaa tällaista törmäystä. Kuvassa kolmesta aivan erityyppisestä digitaalisesta informaatiosta on syntynyt sama tiiviste.
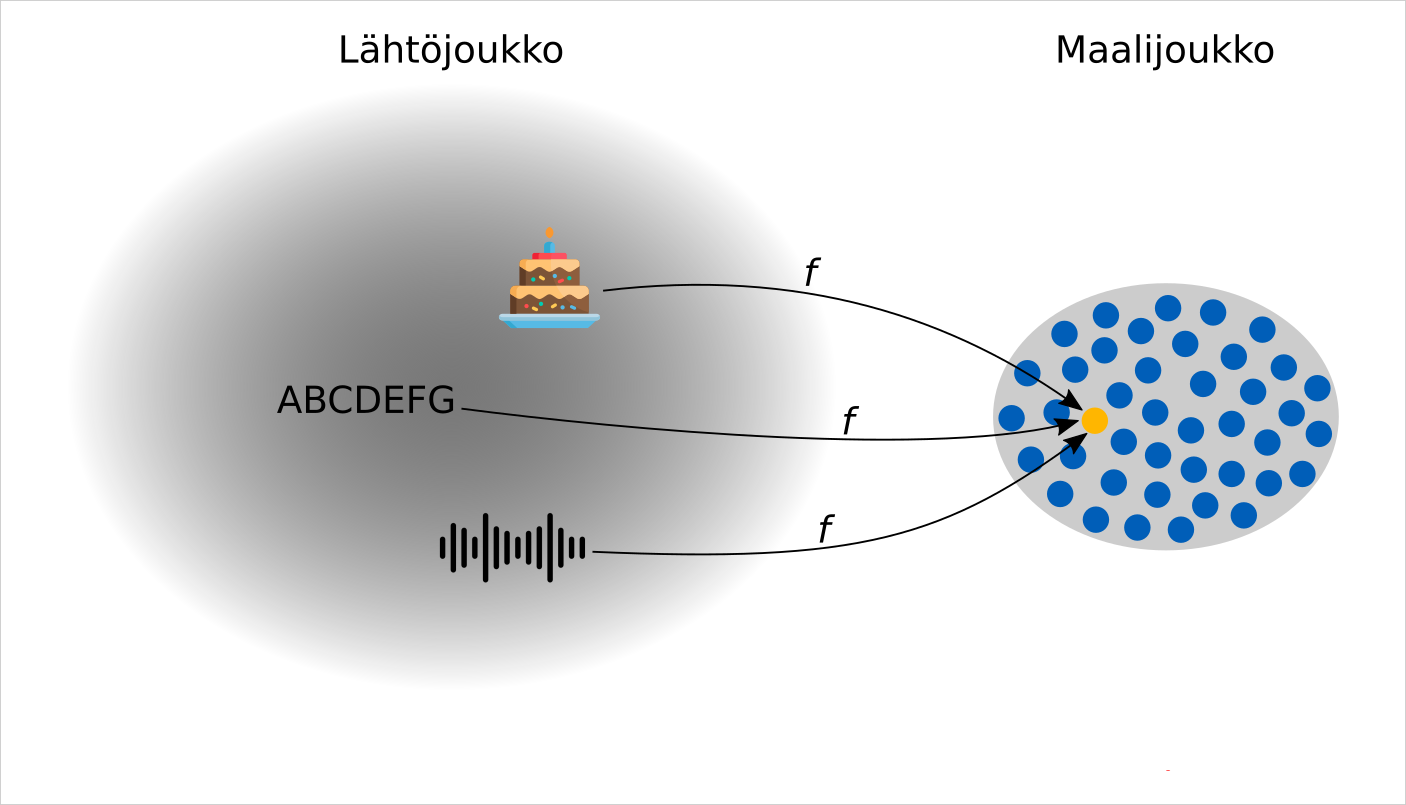
Kuten aiemmin jo mainittiin, on olemassa eri pituisia tiivisteitä. Suuri osa tänä päivänä käytetyistä tiivisteistä on 256-, 384- tai 512-bittisiä.
Tiivistefunktion kykyä sietää törmäyksiä voi kuvata numeerisella luvulla tai bittimäärällä. Käytämme jälkimmäistä. Mitä suurempi luku on, sen epätodennäköisempää on että törmäyksiä tapahtuu.
Käytäntö on osoittanut, että hyvin toimivan tiivistefunktion törmäysten sieto on puolet tiivisteen bittimäärästä. Tällöin esimerkiksi 256-bittisellä tiivisteellä törmäysten sieto on 128 bittiä, eli \(2^{128}\). Vastaavasti 512-bittisellä tiivisteellä törmäysten sito on 256 bittiä, eli \(2^{256}\).
Olemme jo hieman käsitelleet lukuja, jotka ovat suhteellisen suuria. Esimerkiksi kaikkien 128-bittisten avainten läpikäynti brute-force-menetelmällä todettiin haastavaksi. Tästä voi syntyä harha, että tiivistefunktio tuottaisi saman tiivisteen kahdelle alkukuvalle erittäin harvoin.
Tarkastellaan syntymäpäiväparadoksin avulla todennäköisyyttä sille, että törmäys tapahtuu. Syntymäpäiväparadoksi kuvailee seuraavanlaista tilannetta:
On olemassa luokkahuone.
Huoneeseen saapuu yksi oppilas kerrallaan.
Kuinka monta oppilasta vaaditaan, että kahdella oppilaalla on sama syntymäpäivä 50 % todennäköisyydellä?
Sama ilmaistuna hieman matemaattisemmin:
Meillä \(n\) ihmistä luokassa.
Miten todennäköistä on, että kahdella ihmisellä on sama syntymäpäivä?
Havainnollistamisen helpottamiseksi oletamme kalenterivuodessa olevan tasan 365 päivää.
Oletetaan myös, että ihmisten syntymäpäivät olisivat tasajakautuneita. Todellisuudessa syntymäpäivät eivät jakaudu tasaisesti.
Lasketaan todennäköisyys \(P(A)\) tilanteessa, jossa luokassa on kaksi oppilasta.
Kahdella henkilöllä on sama syntymäpäivä todennäköisyydellä \(P(A)\).
Kahdella henkilöllä ei ole samaa syntymäpäivää todennäköisyydellä \(P(A')\).
Luonnollisesti edellisten todennäköisyyksien summa on \(P(A)+P(A') = 1\).
Voimme siis laskea joko todennäköisyyden \(P(A)\) tai vastatodennäköisyyden \(P(A')\).
Näistä voimme aina laskea toisen tapahtuman todennäköisyyden, esimerkiksi \(P(A)=1-P(A')\).
Esimerkkimme laskennassa hyödynnetään vastatapahtumaa, eli sitä että kahdella henkilöllä EI ole sama syntymäpäivä.
Laskentaan määritellään seuraavat reunaehdot:
Jos luokkahuoneessa on vain yksi henkilö, on todennäköisyys samalle syntymäpäivälle tietenkin \(P(A) = 0\).
Jos luokkahuoneessa on 366 henkilöä, todennäköisyys sille, että luokkahuoneessa on vähintään yksi pari jolla on sama syntymäpäivä \(P(A)=1\). Tämä johtuu siitä, että vuodessa on 365 kappaletta mahdollisia syntymäpäiviä.
Mallinnetaan, miten luokkahuoneessa olevien henkilöiden määrä vaikuttaa todennäköisyyteen, että kahdella henkilöllä on sama syntymäpäivä. Tarkastellaan tilannetta \(P(A')\) eli vastatodennäköisyyden näkökulmasta.
Lasketaan todennäköisyydet luokkahuoneessa olevien henkilöiden lukumäärän mukaan.
2 henkilöä luokassa:
Todennäköisyys, että heillä ei ole samaa syntymäpäivää on \(P(A') = \frac{365}{365} \times \frac{364}{365}\).
Tällöin todennäköisyys, että heillä ei ole samaa syntymäpäivää on \(P(A')= 0.99726\).
Todennäköisyys sille, että heillä on sama syntymäpäivä on siis \(P(A)=1-P(A')\), josta \(P(A)= 0.0027\).
3 henkilöä luokassa:
Todennäköisyys, että heillä ei ole samaa syntymäpäivää on \(P(A') = \frac{365}{365} \times \frac{364}{365} \times \frac{363}{365}\).
Tästä saamme todennäköisyydet \(P(A')=0.9917958\) ja \(P(A)= 0.0082\).
Matematiikassa emme ole kiinnostuneet yksittäisistä tapauksista. Yleistämme todennäköisyyden tilanteelle jossa huoneessa on \(n\) henkilöä:
Ei samaa syntymäpäivää \(P(A') = \frac{365}{365} \times \frac{364}{365} \times \cdots \times \frac{365-n+1}{365}\).
Seuraavissa koodisoluissa lasketaan luokkahuoneessa olevien henkilöiden lukumäärän mukaan todennäköisyys sille, että huoneessa olevista henkilöistä joillain on sama syntymäpäivä. Seuraava koodi luo funktion, joka laskee todennäköisyyden \(P(A')\) eli todennäköisyyden, että luokkahuoneessa kahdella henkilöllä ei ole samaa syntymäpäivää.
# Funktio laskee todennäköisyyden
# Että kahdella henkilöllä EI ole samaa syntymäpäivää
# Argumentiksi annetaan henkilöiden määrä luokkahuoneessa.
def p_bar(n=100):
# Jos huoneessa on enemmän ihmisiä kuin vuodessa päiviä
# On vähintään kahdella henkilöllä varmasti sama syntymäpäivä.
if n > 365:
return 0.0
# Aluksi ei ole todennäköistä että henkilöillä on sama syntymäpäivä
ei_syntymäpäiviä_tn = 1.0
# Jokainen henkilö luokkahuoneessa pienentää todennäköisyyttä sille,
# että kahdella henkilöllä on sama syntymäpäivä.
for i in range(n):
ei_syntymäpäiviä_tn *= (365-i)/365
# Palautetaan todennäköisyys että kahdella henkilöllä huoneessa ei ole samaa syntymäpäivää.
return ei_syntymäpäiviä_tn
print("P(A') funktio luotu.")
Seuraava koodi luo funktion, joka laskee annettun henkilömäärän mukaisen todennäköisyyden, että luokkahuoneessa kahdella henkilöillä on sama syntymäpäivä.
def syntymäpäivä(henkilöitä):
print("Näytetään todennäköisyydet P(A) \n")
print("Henkilömäärä P(A)")
for n in henkilöitä:
n_tn = p_bar(n)
print(" {:3} {:.7f}".format(n, 1-n_tn))
print("Syntymäpäivien todennäköisyydet näyttävä funktio luotu.")
Seuraavaksi määritellään henkilömäärä ja kutsutaan syntymäpäivä-funktiota.
from xip import syntymäpäivä
# Luodaan taulukko mielenkiintoisista henkilömääristä tarkasteluun.
henkilöitä = [i for i in range(1,25,1)] + [i for i in range(30,100,10)] +[i for i in range(100,400,100)]+ [350, 365]
# Lasketaan todennäköisyys annetuille henkilömäärille samalle syntymäpäivälle luokassa.
syntymäpäivä(henkilöitä)
Yllä näkyvä tulos saattaa yllättää. Vaikka vuodessa on 365 päivää, niin jo varsin pienillä henkilömäärillä todennäköisyys sille, että kahdella henkilöllä on sama syntymäpäivä, on merkittävä. Vastaa seuraaviin syntymäpäiväparadoksia käsitteleviin kysymyksiin.
Nyt voimme siis hyväksyä sen tosiasian, että tiivisteet voivat törmätä.
Tarvittaessa voimme ehkä jopa laskea,
mikä on todennäköisyys tiivisteiden törmäykselle jos tuotamme esimerkiksi \(2^{80}\) tiivistettä.
Älä kuitenkaan käytä esimerkkikoodin p_bar funktiota,
koska se ei tule saamaan laskentaa valmiiksi suurille luvuille.
Voimmeko laskea tiivisteestä alkukuvan?¶
Oletetaan, että saamme laskettua informaatiosta A tiivisteen X, ja myöhemmin saamme eri informaatiosta B laskettua saman tiivisteen X. Pystymme siis tuottamaan törmäyksen. Matemaattisesti tiivistefunktioilla ei ole olemassa käänteisfunktiota, jolloin ei myöskään ole olemassa tapaa laskea alkukuvaa.
Mietitään hypoteettista skenaariota, jossa osoittautuu että jokin tiivistefunktio on sellainen, että sillä olisi matemaattisen heikkouden kautta olemassa käänteisfunktio. Mitä tästä seuraisi? Tästä ei olisi suurempaa iloa, koska alkukuvia jotka tuottavat saman tiivisteen X, on rajattomasti. Meillä on siis ääretön määrä alkukuvia, joita voimme tuottaa, mutta emme pysty sanomaan mikä niistä on juuri se oikea.
Käänteisfunktion löytämistä todennäköisempää on keksiä menetelmä, jolla voi tuottaa törmäyksiä eli alkukuvia, joista tulee sama tiiviste. Jos näin tapahtuu, tuollaisen tiivistefunktion käyttö lopetettaisiin. Näin on jo käynyt usealle aiemmin käytetylle tiivistefunktiolle.
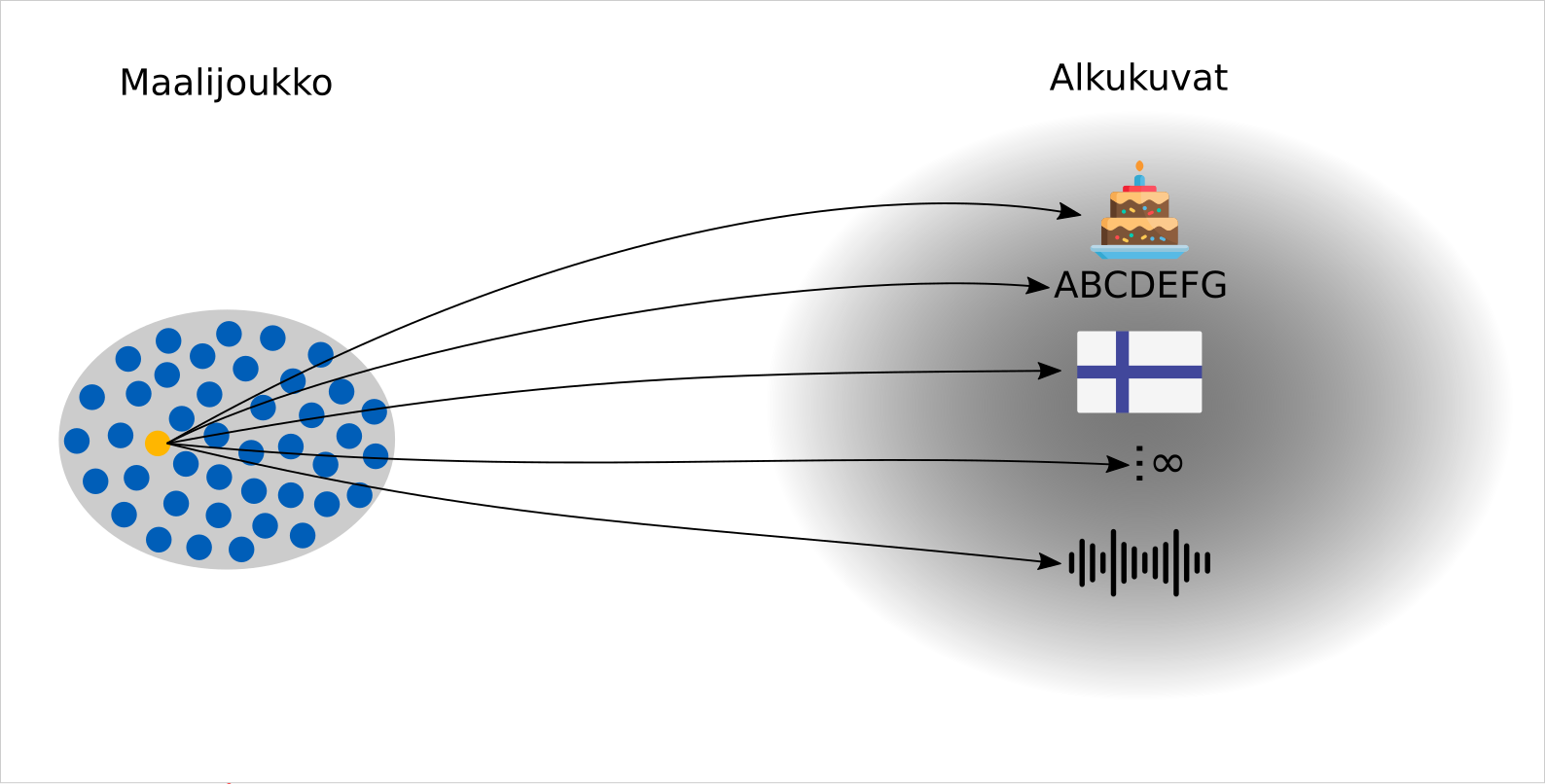
Voi olla, että tekstit ”Tuo maitoa kaupasta!” ja ”Löysin tämän vuosikymmenen parhaimman bändin ja lähden heidän keikalleen!!!”, tuottavat jollain tiivistefunktiolla saman tiivisteen.
Mitä sitten tarkoittaa äärettömyys tässä yhteydessä?
Saman tiivisteen on pystynyt laskemaan miljardeista ja miljardeista kuvatiedostoista, äänitiedostoista, tekstitiedostoista yms. Ääretön tarkoittaa nyt tässä tapauksessa sitä, että meillä on rajoittamaton määrä mahdollisia alkukuvia, joista mikä tahansa voi olla se oikea alkukuva.
Yhteenveto¶
Nyt tiedämme, että alkukuvia on ääretön määrä ja että niistä lasketaan lyhyehkö tiiviste. Opimme myös sen, että tiivistefunktion tuottamasta tiivisteestä ei pysty tuottamaan alkuperäistä oikeaa alkukuvaa. Tämän lisäksi tiivisteet voivat myös törmätä.
Tiivisteitä käytetään paljon tiedon salauksessa ja suojauksessa. Katsotaan seuraavaksi käytännössä, millaisia tiivistefunktioita on olemassa.