Kurssin viimeisimmän version löydät täältä: Johdatus kryptografiaan: 2024
Tietokone ja satunnaisuus¶
Miten tietokoneella tuotetaan aitoja satunnaislukuja?
Määritelmiä¶
Tässä osiossa käytetään useita ehkä entuudestaan tuntemattomia termejä. Ohessa niiden määritelmät.
- Satunnaislukugeneraattori:
Satunnaislukugeneraattori (Random Number Generator - RNG) tuottaa satunnaislukuja. Tuotetut satunnaisluvut voivat olla joko aitoja satunnaislukuja tai näennäissatunnaisslukuja.
- Aito RNG:
Aito satunnaislukugeneraattori (True Random Number Generator - TRNG) käyttää tietokoneen havaitsemia fyysisen maailman ilmiöitä tuottaessaan satunnaisluvun. Tietokone kerää dataa esimerkiksi hiiren liikkeestä, näppäimistön painalluksista, verkkokortin pakettien aikavälien vaihtelusta yms. Aitojen satunnaislukujen tuottaminen on hidasta ja siksi aitoja satunnaislukuja käytetään säästeliäästi. Käyttökohteita ovat esimerkiksi kryptografisen avaimen, kertakäyttöluvun tai siemenluvun tuottaminen.
- Näennäis-RNG:
Näennäissatunnaislukugeneraattori (Pseudo Random Number Generator - PRNG) tuottaa satunnaislukuja siemenluvusta deterministisellä eli ennakkoon määritellyllä algoritmilla. PRGN:llä tuotettuja satunnaislukuja käytetään paljon kryptografian ulkopuolella ja harkiten myös kryptografiassa. PRNG on täysin deternimistinen, eli samalla siemenluvulla tuotetaan aina sama näennäissatunnaisluku. Käytännössä on olemassa tapa saada selville kaikki edelliset ja seuraavat tuotetut satunnaisluvut jos PRNG:n toiminta on tunnettu ja saatavilla on yksi tuotettu satunnaisluku.
- Kryptografisesti turvallinen PRNG:
Kryptografisesti turvallinen satunnaislukugeneraattori (Cryptographically Safe Pseudorandom Number Generator - CSPRNG) on deterministinen, mutta hyödyntää aitoa satunnaisuutta. CSPRNG:n tuottamasta satunnaisluvusta tai lukujoukosta ei voi päätellä edellisiä tai seuraavia tuotettuja satunnaislukuja.
- Satunnaisuus:
RNG:n tuottamaa lukua sanotaan satunnaiseksi jos:
Jokaisen mahdollisen luvun todennäköisyys on yhtä suuri. Tällöin jos luvut voivat olla väliltä \(1-N\) niin jokaisen luvun todennäköisyys on \(\frac{1}{N}\) .
RNG:n tuottamasta luvusta tai lukusarjasta ei pysty päättelemään edellistä eikä seuraavaa numeroa tai numerosarjaa.
- Jakauma:
Yksi tapa tutkia satunnaislukugeneraattorin tuottamien satunnaislukujen hyvyyttä on tarkastella lukujen jakaumaa. Jakaumasta pyritään tarkistamaan, tuottaako satunnaislukugeneraattori yhtä paljon kaikkia arvoja. Jos jakaumasta näkee että pieniä lukuja on enemmän kuin suuria lukuja, kannattaa kryptografista avainta arvailla pienillä luvuilla.
- Entropia-allas:
Aitojen satunnaislukujen tuottaminen on hidasta. Siksi tietokoneen käyttöjärjestelmä pyrkii tuottamaan jatkuvasti aitoja satunnaislukuja, jotka se tallentaa entropia-altaaseen. Entropia-allas on aitojen satunnaislukujen sijainti yleisimmissä käyttöjärjestelmissä. Kun pyydämme käyttöjärjestelmältä aitoa satunnaislukua, se käyttää entropia-altaaseen tallennettuja lukuja entropian lähteenä.
Tietokone suorittaa laskuoperaatioita deterministisesti eli lainalaisesti. Joka kerta kun tietokone suorittaa esimerkiksi laskentaoperaation kokonaisluvuilla 2+3, tulokseksi tulee 5 ellei laskennassa tapahdu vakavaa virhettä.
Miten tietokoneella voidaan tuottaa satunnaisuutta? Tutkitaan kahta tapaa, joista ensimmäinen ei ole kryptografisesti turvallinen ja joista toinen voi olla kryptografisesti turvallinen. Menetelmien tai algoritmien todistaminen turvalliseksi on oma kryptografian tutkimusala.
Näennäissatunnaisuus (PRNG)¶
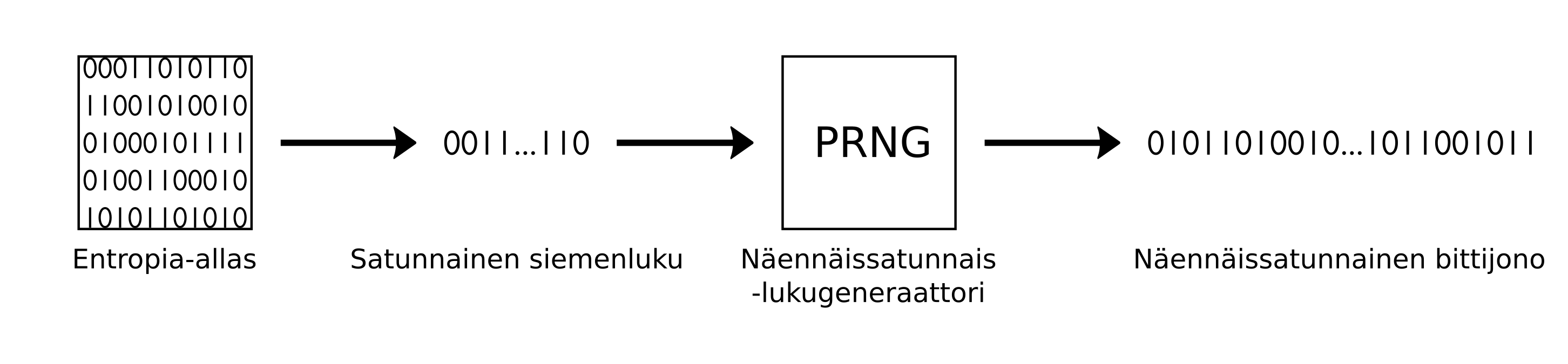
Tietokoneen satunnaislukufunktiot, kuten esimerkiksi Python-kirjaston randint, kuuluvat
näennäissatunnaisten satunnaislukugeneraattorien ryhmään (engl. pseudorandom number generator, PRNG).
Algoritmi, joka tuottaa satunnaislukuja, ottaa syötteeksi siemenluvun (engl. seed) ja laskee deterministisesti tämän pohjalta satunnaiselta vaikuttavan luvun.
Tietokoneen laskentaoperaatioiden deterministisyys tarkoittaa, että asiat ovat kausaalisia. Niillä on siis syy-seuraussuhde. PRNG toteutetaan yleensä niin, että laskenta tapahtuu kunnassa modulo-renkaan sisällä ja hajauttava funktio voi olla esimerkiksi polynomi, eksponentointi tai jokin muu vastaava matemaattinen operaatio. Jos asia kiinnostaa enemmän, voit etsiä lisää tietoa netistä. Toimivia hakusanoja ovat esimerkiksi pseudorandom function, pseudorandom generation ja Mersenne Twister. Mersenne-twisteristä (MT) on paljon tietoa saatavilla ja se on hyvä esimerkki PRNG:n kehityskaaresta. MT:tä on tutkittu runsaasti ja vaikka sitä on paranneltu, se on lopulta havaittu turvattomaksi. Siksi sen käyttöä ei enää suositella.
Tietokoneen käyttöjärjestelmä sekä ohjelmointikielen kirjastot toteuttavat satunnaisuutta omalla tavallaan. Voit lukea lisää miten Python-kielen sisäänrakennettu kirjasto tai numeerisen laskennan kirjasto toteuttavat PRNG toiminnallisuutta. Näiden kirjastojen funktiot ja PRNG:t eivät tuota kryptografisesti turvallisia satunnaislukuja.
Kokeillaan PRNG:n toimintaa:
Voit halutessasi muuttaa satunnaislukugeneraattorille menevää siementä asettamalla
siemenmuuttujaan esimerkiksi oman syntymäaikasi.Siemenellä määritetään PRNG:lle arvo, jonka mukaan se tuottaa seuraavan näennäissatunnaisluvun.
Koodissa for-silmukassa PRNG alustetaan jokaisella satunnaislukugeneraattorin kutsukerralla samalla siemenllä.
Koska siemen on sama, tuottaa deterministinen PRNG aina saman näennäissatunnaisluvun.
import random
from numpy import binary_repr
# Satunnaisen bittikuvion bittien määrä
bittejä = 22
# Satunnaisluvun alustaminen
siemen = 20221206 # <- muuta halutessasi tähän oma syntymäaikasi vvvvkkpp
random.seed(siemen)
print("Haetaan samalla siemenellä viisi PRNG:n tuottamaa bittikuviota")
for i in range(5):
print("Siemen {}: bittikuvio: 0b{} ".format(siemen,binary_repr(random.getrandbits(bittejä),bittejä)))
random.seed(siemen) # Alustetaan satunnaislukugeneraattori taas samalla siemenellä
Yllä olevasta esimerkistä nähdään, että deterministinen satunnaislukugeneraattori tuottaa samalla satunnaislukugeneraattorin siemenellä aina saman arvon. Yksi tapa käyttää PRNG:tä on alustaa siemen, minkä jälkeen tuotetaan yksi ”erä” näennäissatunnaisia lukuja. Ohjelmoidessa toinen tapa alustaa PRNG on kutsua ohjelmointikirjaston funktiota ilman argumenttia. Tällöin PRNG yleensä käyttää tietokoneen sen hetkistä kellonaikaa siemenenlukuna.
Nämä kaksi koodisolua ovat ensimmäinen konkreettinen esimerkki siitä, että yksinkertaistakin ohjelmointikielen tai käyttöjärjestelmän funktiota on osattava käyttää oikein.
import random
from numpy import binary_repr
# Satunnaisen bittikuvion bittien määrä
bittejä = 64
# Satunnaisluvun alustaminen
print("Siemen alustetaan tietokoneen ajalla.")
random.seed() # Tässä käytämme ympäristömme sen hetkistä kellonaikaa siemenenä
print("PRNGn sisäinen tila muuttuu joka kerta seuraava näytettä pyytäessä.")
for i in range(5):
print("Bittikuvio: 0b{} ".format(binary_repr(random.getrandbits(bittejä),bittejä)))
Joka kerta kun ajat edellisen koodisolun, ohjelma tuottaa sen hetkisen kellonajan perusteella siemenen PRNG:lle, joka tuottaa siitä näennäissatunnaisluvun.
Kryptografisesti turvallinen näennäissatunnaislukugeneraattori¶
Yksi edellä esitellyn PRNG:n heikkous on, että saadessasi selville yhden PRNG:llä tuotetun satunnaisluvun tai lukusarjan, sinun on mahdollista laskea seuraavat ja edelliset näennäissatunnaisluvut.
Kryptografisesti turvallinen näennäissatunnaislukugeneraattori (engl. cryptographically safe pseudorandom number generator, CSPRNG) on toteutettu siten, ettei yhden luvun tai lukusarjan näkeminen auta päättelemään seuraavia tai edellisiä CSPRNG:n tuottamia näennäissatunnaislukuja.
Aito satunnaisuus tietokoneessa¶
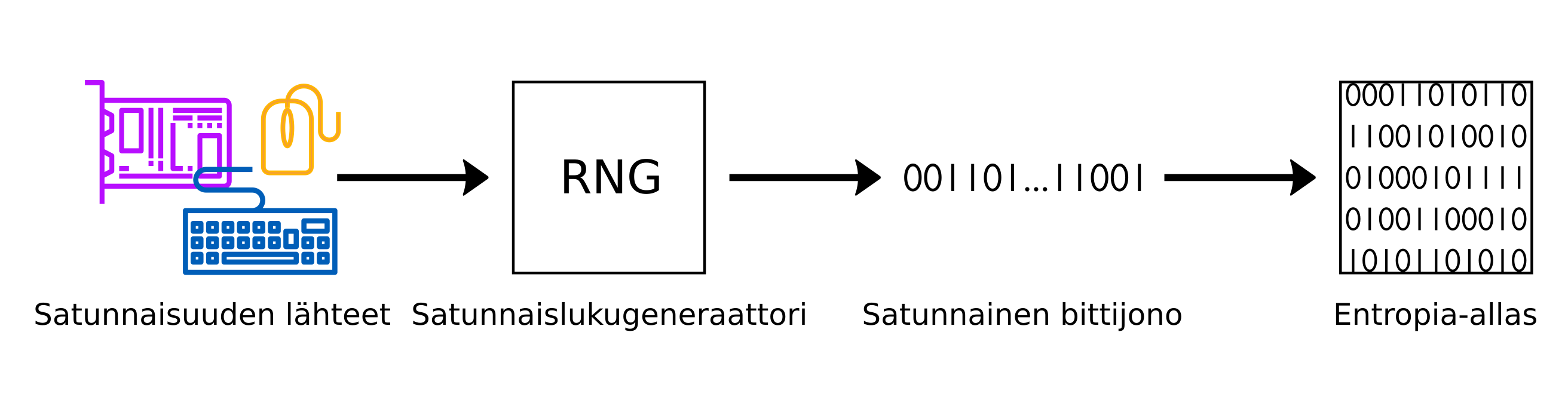
Aitojen satunnaislukujen tuottaminen tietokoneella on verrattain hidasta ja siksi aitoja satunnaislukuja käytetään säästeliäästi. Siemenet tai syötteet aitojen satunnaislukujen tuottamiseen kerätään reaalimaailman ilmiöistä. Tällaisia tietokoneen rekisteröimiä ilmiöitä ovat esimerkiksi näppäimien painallukset, hiiren liikkeet, verkkokortin pakettien aikavälin vaihtelu ja tietokoneen keskeytysten vaihteluväli. Kun satunnaislukugeneraattori on kerännyt näitä ilmiöitä riittävästi, se tuottaa satunnaisia bittikuvioita, jotka kerätään entropia-altaaseen. Jos tietokone ei saa tarpeeksi reaalimaailman dataa, aitojen satunnaislukujen tuottaminen ja tallentaminen entropia-altaaseen kestää pidempään.
Tällaisesta entropia-altaasta voi pyytää siemenlukua, joka on aidosti satunnainen. Entropia-altaaseen tulee bittejä tipoittain, eikä sitä voi käyttää suoraan ihan kaikkeen satunnaisuutta vaativaan toimintaan. Jos Entropia-altaasta käytetään bittejä liian nopeasti, se voi ”ehtyä”. Kiinnostuneiden kannattaa perehtyä tähänkin aiheeseen tarkemmin – varsinkin jos on tekemisissä virtuaalikoneiden kanssa, jotka käynnistyvät nopeasti ja haluavat heti käytettäväkseen hyviä satunnaislukuja.
Useat verkosta löytyvät palvelut toimivat virtuaalikoneiden tai virtualisointien avulla, jolloin niillä ei ole välttämättä mahdollisuutta kerätä reaalimaailman ilmiöitä. Esimerkiksi pilvilaskennassa käytetyt virtualisoidut pikafunktiot ovat haastavia, koska näiden palveluiden pitää vastata verkosta tuleviin kyselyihin millisekunneissa. Tällöin ei ole aikaa kerätä satunnaisuutta reaalimaailman ilmiöistä. Usein mikropalveluille ja virtuaaliympäristöille on tarjottava aitoja satunnaislukuja jollain muulla tavalla. Tällaisten aitojen satunnaislukujen on oltava välittömästi saatavilla palvelun käynnistyessä.
Osa mikroprosessoreista sisältää aitoja satunnaislukuja tuottavia fyysisiä rakenteita. Tämän lisäksi on olemassa tuotteita sekä ratkaisuja, jotka kykenevät tuottamaan aitoja satunnaislukuja esimerkiksi pilvipalveluoperaattoreille. Tällöin pilvipalvelussa käynnistyvä virtuaalikone tai mikropalveluarkkitehtuurin lambda-funktio saa välittömästi aidosti satunnaisen luvun. Voit etsiä tällaisista ratkaisuista tietoa hakusanalla True Random Number Generator.
Hyviä siemenlukuja Pythonilla¶
Python hyödyntää käyttöjärjestelmän entropia-allasta (Linuxissa /dev/urandom ja /dev/random). Pythonin os.urandom() -funktio suorittaa lukusarjan hakemisen lisäksi hallinnoivia toimenpiteitä. Tässä vaiheessa oletamme, että saavutamme riittävän satunnaisuuden tätä entropia-allasta käyttävän satunnaislukugeneraattorin avulla. Asia ei tietenkään ole näin yksinkertainen, mutta tässä vaiheessa tämä riittää tarpeisiimme.
Alla lyhyt esittely toimenpiteistä, jotka oheisen koodisolun ajaminen suorittaa:
Määritellään haettavien satunnaislukujen määrä tavuina (oletusarvo 10 tavua). Yksi tavu on 8 bittiä.
Haetaan satunnaisluvut käyttöjärjestelmän satunnaisuutta hyödyntäen os.urandom()
Tulostetaan haetut satunnaiset tavut ja näytetään tavuja vastaava ASCII-kirjainmerkki. Aiemmin opimme, että ASCII-taulukko sisältää sekä tulostuvia merkkejä että ohjausmerkkejä. Siksi on mahdollista, että
merkkinä-kohtaan ei tulostu ymmärrettävää tai näkyvää kirjainsymbolia.
# Otetaan käyttöön kirjastot
import os
from numpy import binary_repr
tavuja = 10 # Haettavien tavujen määrä
csprng = os.urandom(tavuja) # Tässä haetaan satunnaisluvut entropia-altaasta
print("{} tavua aitoja satunnaisia bittejä haettu!".format(tavuja))
print("\nTavuina, ja merkkeinä (jos mahdollista), sekä bitteinä nämä satunnaisluvut näyttävät seuraavalta:\n")
for byte in csprng:
print("byte:{:4} merkkinä:{:3} binäärinä: 0b{}".format(hex(byte), chr(byte), binary_repr(byte,8)))
Mikä on satunnaista?¶
Tässä osiossa esitellään muutama esimerkki satunnaisuuden hahmottamiseksi. Tehdään pieni ajatuskoe:
Oletetaan, että haluamme aidon satunnaisluvun eli käytännössä satunnaisen bittikuvion.
On olemassa monia algoritmeja ja palveluita, joita voimme hyödyntää satunnaisluvun hankkimiseksi.
Miten voimme varmistua, että saamamme satunnaisluku on tuotettu hyvällä satunnaislukugeneraattorilla?
Matematiikassa on useita erilaisia satunnaisuuden määritelmiä. Tässä muutama satunnaisluvun tunnusmerkki kurssillemme.
Jos satunnaislukugeneraattori tuottaa lukuja välillä 0…N, jokasiella luvulla on sama odotusarvo \(\frac{1}{N}\):
Sama odotusarvo tarkoittaa sitä, että kun satunnaislukugeneraattori on tuottanut tarpeeksi suuren määrän satunnaislukuja (frekvenssianalyysin näkökulmasta) jokaista mahdollista lukua esiintyy yhtä paljon. Tällöin kaksi seuraavaa lukujonoa 0, 1, 2, 3 ja 1, 3, 2, 0 täyttävät ehdot.
Samaa lukua voi esiintyä useasti peräjälkeen satunnaislukujonossa. Tällöin esimerkiksi lukujono 8, 2, 1, 1, 4, 6, 2, 9, 7, 4, 0, 3, 5 on täysin mahdollinen realisaatio satunnaislukugeneraattorin tuottamista satunnaisluvuista.
Vastakohtana lukujono 0, 0, 0, 0, 0, 0, 1, 0, 0, 99 ei ole esimerkki hyvästä lukujonosta, koska 0 esiintyy huomattavasti useammin kuin mikään muu luku.
Satunnaislukugeneraattorin tuottamissa satunnaisluvuissa ei ole ilmiselvää kuviota (engl. pattern):
Tällöin esimerkiksi lukujono 0, 1, 2, 3 on huono, koska seuraava luku on todennäköisesti 4. Seuraava luku voi myös olla 0 jos numeroavaruus on neljällä jaollinen, eli \(\pmod{4}\).
Samoin myös lukujono 5, 5, 5, 1, 5, 5, 5, 100, 5, 5, 5, 678, 5, 5, 5, 2 on huono kahdesta syystä: a) numero 5` on yliedustettu ja b) numero 5 esiintyy aina kolmen ryhmissä.
Satunnaislukugeneraattorilla tuotetun satunnaisluvun tai satunnaislukujonon perusteella ei voi päätellä mikä oli edellinen tai mikä tulee olemaan seuraava satunnaisluku:
Oletetaan että satunnaislukugeneraattori tuottaa lukujonon 0, 7, 0, 6, 0, 5. Jos seuraavat sen tuottamat luvut ovat 0, 4, 0, 3, voimme olettaa että tämän jälkeen tulevat luvut 0, 2, 0, 1. Vastaavasti voimme olettaa, että satunnaislukugeneraattori on aiemmin tuottanut luvut 0, 9, 0, 8. Pystymme siis päättelemään sekä seuraavan luvun että seuraavan lukusarjan. Samoin voimme päätellä edellisen luvun ja edelliset lukusarjat. Tämä on esimerkki huonosta RNG:stä.
Satunnaisuus ja kryptografia¶
Miksi kryptografian kurssilla puhutaan satunnaisluvuista, satunnaisuudesta ja vaikeasti ennustettavista lukusarjoista?
Kryptografisen avaimen oletetaan olevan ainutlaatuinen, eikä sitä pitäisi pystyä päättelemään millään keinolla. Sen siis halutaan olevan hyvä satunnaisluku.
Kryptografisten salaimien ja algoritmien oletetaan tuottavan satunnaisen näköistä informaatiota. Jos salain toimii hyvin, sen tuottama salakieli muistuttaa kohinaa, jossa kaikkia lukuja (tai bittejä) esiintyy yhtä todennäköisesti (tai yhtä paljon).
Kryptografisen salaimen halutaan toimivan siten, että jos kahdessa salattavassa selväkielessä on yhden bitin ero, niistä tuotetuissa kahdessa salakirjoituksessa puolet biteistä ovat eri tilassa.
Kryptografisia avaimia tuotetaan esimerkiksi satunnaislukugeneraattoreilla. Satunnaislukugeneraattoreita kehitetään jatkuvasti ja niitä tutkitaan useilla eri menetelmillä.
Satunnaislukujen hyvyyden arvioimiseen on olemassa tilastollisia testejä, mutta niillä voidaan vain varmistua ettei käytetyssä satunnaislukugeneraattorissa ole ilmiselviä heikkouksia. Näiden tilastollisten testien läpäiseminen tarkoittaa, että satunnaislukugeneraattori näyttää tuottavan hyviä satunnaislukuja. Vaikka kokeilisimme kaikki tunnetut satunnaisuutta testaavat menetelmät, se ei silti tarkoita että jokin satunnaislukugeneraattori olisi absoluuttisesti hyvä.
Yhteenveto¶
Nyt ymmärrämme, mitä ovat satunnaislukugeneraattori ja satunnaisluku, ja millainen ero on aidolla sekä näennäissatunnaisella luvulla. Lisäksi tiedämme, että on olemassa kryptografisesti turvallisia satunnaislukugeneraattoreita.
Seuraavassa opetusmoduulissa hyödynnämme nyt satunnaisuudesta oppimiamme asioita ja tutkimme kryptografisia avaimia, jotka ovat kryptografisten menetelmien ainoa salainen osa.