Moduloaritmetiikka¶

Modulo \(\pmod{n}\)¶

Modulolaskenta on laskentaa kokonaislukujen jakojäännöksillä.

Peruskoulusta tutulla tavalla jaettaessa kokonaisluku \(a\) toisella kokonaisluvulla \(n\) saadaan tulokseksi kokonaisluku \(b\) sekä jakojäännös \(c\). Eli voidaan sanoa että \(a\):

\[a = b \cdot n + {\bf c}\]

Joka voidaan esittää myös seuraavasti:

\[\frac{a}{n} = b + \frac{\bf c}{n}\]

missä \(\textbf{c}\) on kokonaisluku välillä 0 ja \(n-1\). Tätä \(\textbf{c}\):tä kutsutaan jakojäännökseksi eli moduloksi. Lukua \(n\) kutsutaan usein modulukseksi. Merkitsemme modulusta yhtälöissä notaatiolla \(\pmod{n}\) .

Esimerkki: Toteutetaan modulon laskenta \(a=17\), \(n=3\) arvoilla. Eli toteutamme laskennan:

\[ \begin{align}\begin{aligned}17 = 5 \cdot 3 + {\bf 2}\\\frac{17}{3}= 5 + \frac{\bf 2}{3}\end{aligned}\end{align} \]

jolloin jakojäännös, eli modulo on 2. Tässä suoritimme laskennan \(17 \pmod{3}\) .

Python-koodilla tämä tapahtuu seuraavasti:

Inactive

a = 17    # Jaettava
n = 3     # Jakaja (eli modulus)
b = a//n  # Lasketaan kokonaisluku
c = a%n   # Lasketaan modulo

# Tulostetaan esimerkin tulos:
print("Jaettava     a:", a)
print("Jakaja       n:", n)
print("Kokonaisluku b:", b)
print("Modulo       c:", c)

Tehtävä:

Kongruenssi \(\equiv\)¶

Sanotaan, että kaksi lukua ovat kongruentit modulo \(\textbf{n}\), jos (ja vain jos) niillä on sama jakojäännös jaettaessa luvulla \(n\).

Esimerkiksi luvut 11 ja 126 ovat kongruentit modulo 5, koska \(11 \pmod{5} = 1\) ja \(126 \pmod{5} = 1\). Tällöin voidaan sanoa, että 11 ja 126 kuuluvat samaan jäännösluokkaan modulo 5.

Samoin jaettavat 5, 8 ja 11 kuuluvat samaan jakojäännösluokkaan 2, kun jakajana on luku 3:

\[ \begin{align}\begin{aligned}2 \equiv 5 \pmod{3}\\2 \equiv 8 \pmod{3}\\2 \equiv 11 \pmod{3}\end{aligned}\end{align} \]

Kaikkien edellisten jakojäännösluokka on 2.

Seuraavaksi esitellään kongruenssin testaus Python-koodilla.

Inactive

a_1 = 11      # Ensimmäinen jaettava luku
a_2 = 126     # Toinen jaettava luku
n   = 5       # Jakaja

b_1 = a_1//n  # Ensimmäisen jaettavan luvun kokonaisluku
c_1 = a_1%n   # Ensimmäisen jaettavan luvun jakojäännös - MODULO

b_2 = a_2//n  # Toisen jaettavan luvun kokonaisluku
c_2 = a_2%n   # Toisen jaettavan luvun jakojäännös - MODULO

# Näytetään laskut
print("Luku {:3} jaettuna {}:lla -> kokonaisluku {:2} ja modulo {}".format(a_1, n, b_1, c_1))
print("Luku {:3} jaettuna {}:lla -> kokonaisluku {:2} ja modulo {}\n".format(a_2, n, b_2, c_2))

# Testataan kongruenssi, huomaa miten unicode-merkkejä voi käyttää print-funktiolla
if c_1 == c_2:
    print("Luvut {} ja {} ovat kongruentit modulo {}, eli\nluvut {} ja {} \u2261 modulo {}, ja kuuluvat samaan jäännösluokkaan modulo {}".format(a_1, a_2, n, a_1, a_2,n, n))
else:
    print("Luvut {} ja {} eivät ole kongruentit modulo {}, eli {} ja {} \u2262 modulo {}".format(a_1, a_2, n, a_1, a_2, n))

Modulo kokonaislukujoukoilla¶

Otetaan kaikkien kokonaislukujen joukko \(-\infty\) \(+\infty\). Tällaisella äärettömällä lukujoukolla ei luonnollisesti olekaan pienintä tai suurinta arvoa.

\[..., -7, -6, -5 , -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, ...\]

Kun luvut korvataan jakojäännöksillä, saadaan syklisesti etenevä sarja lukuja 0:sta n-1:een. Esimerkiksi \(n=5\) tapauksessa:

\[..., 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 4, 0, 1, ...\]

Eli aina kun päästään luvun \(n\) monikertaan, ”pyörähdetään” takaisin nollaan. Nyt ääretön lukujoukko on muuttunut äärelliseksi, jonka pienin arvo on \(0\) ja suurin \(n-1\) , eli tässä tapauksessa arvo \(4\). Huomaathan negatiivisten lukujen modulon? Myös ne myös käyvät nollasta \(n-1\):een. Näihin emme ole aiemmin juuri kiinnittäneet huomiota, mutta negatiiviset luvut toimivat aivan samoin kuin positiiviset.

\[-1 \equiv 4 \pmod{5}\;\text{, koska}\;-1 = -1 * 5 + 4\]

Jakojäännös, eli modulo, ei ole koskaan negatiivinen.

Modulo voidaan siis ajatella kehäksi, jonka kehällä ovat kokonaisluvut nollasta \(n-1\):een.

Modulon hahmottaminen¶

Tästä päästäänkin erääseen jokaiselle tuttuun tapaan hahmottaa modulolaskentaa. Normaalissa kellotaulussa nimittäin tunnit ovat modulo 12. Poiketen digitaalisen maailman laskutyylistä, kellotaulussa nollan sijasta yleensä käytetään 12:ta, eli ajat saavat arvoja väliltä 1 - 12.

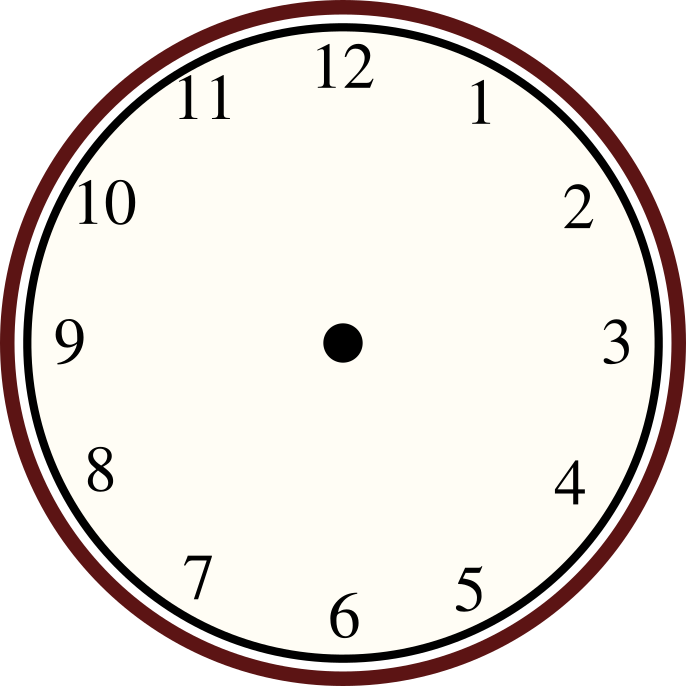
Jos kellon tuntiviisari osoittaa klo 11:ta, niin 3 tunnin kuluttua se näyttääkin kello 2:ta, koska

\[11+3 = 14 \equiv 2 \pmod{12}\]

Tai jos tuntiviisari osoittaa nyt klo 4:ää, niin kahdeksan tuntia sitten se osoitti klo 8:aa, koska

\[4 - 8 = -4 \equiv 8 \pmod{12}\]

Tai jos viisari nyt osoittaa nyt klo 3:a, niin 669 tunnin kuluttua se osoittaa klo 12:ta, koska

\[3+669 = 672 \equiv 0 \pmod{12}\]

Miten modulo liittyy kryptografiaan?¶

Kysymys tietysti kuuluu, että miten tämä liittyy kryptografiaan? Vastaus on, että hyvin monella tapaa, koska modulolaskentaa hyödynnetään lukuisissa salausmenetelmissä.

Pian esiteltävä Caesar-salain voidaan esittää modulon avulla. Aakkoston kaikille 29:lle kirjaimelle annetaan aakkosen esiintymisjärjestystä vastaava indeksi: \(A=0, B=1, C=2, D=3, ..., Å=26, Ä=27, Ö=28\). Tällöin Caesar-salaus määritellään matemaattisesti siten, että \(c_i = (p_i + 3) \pmod{29}\), missä \(p_i\) on selväkielen \(i\):nnes kirjain, ja \(c_i\) on vastaava kirjain salakielessä. Salauksen purku vastaavasti määritellään seuraavasti: \(p_i = (c_i - 3) \pmod{29}\).

Jossain vaiheessa aakkoston ”reuna” tulee vastaan, ja tällöin jatketaan aakkoston vastaikkaisesta päästä. Voit kuvitella, että aakkoset ovat valintakiekon reunalla, jota pyörität vaikkapa kolmen askeleen verran etsiessäsi substituutiota. Laskettaessa äärellisillä lukukentillä logiikka on aina sama kuin kellotaulussa.

Inactive

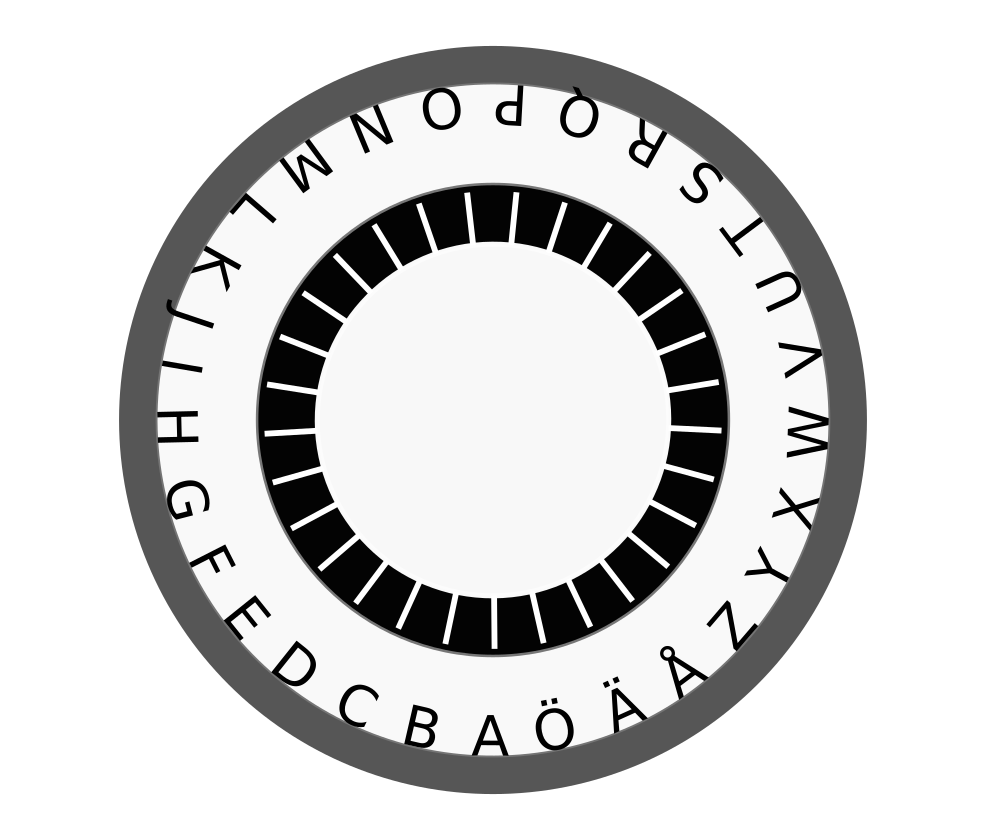
# Kokeillaan aakkoston modulus
from xip import merkistot
import numpy as np

# Luodaan aakkoset
aakkoset, _ = merkistot(suomi=True)

# Luodaan modulus
n = len(aakkoset)

# Lasketaan aakkosten indeksit
indeksit = np.arange(len(aakkoset))

# Tehdään siirros indekseille modulo n
siirros = 3   # <-- Joudut vaihtamaan tätä indeksia tehtävässä
muutetut_indeksit = (indeksit - siirros)%n

# Tulostetaan selväkielen aakkoset ja salakielen korvaavat aakkoset
print("Selväkieliaakkoset:", aakkoset)
print("Salakieliaakkoset :", "".join([aakkoset[i] for i in muutetut_indeksit]))

# Yllä on käytetty list comprehension tapaa tuottaa lista, kannattaa googlata se.

Modulo binääriluvuilla¶

Myös binääriluvuilla modulon laskenta voidaan määritellä vastaavasti: \(c_i = (p_i + k_i) \pmod{n}\) ja \(p_i = (c_i - k_i) \pmod{n}\).

Binääriluvuilla käytetään jakajaa (modulusta) \(n=2\), jolloin esimerkiksi \(c_i\) saa arvon 0 tai 1 seuraavasti:

\(c_i = p_i\) kun \(k_i = 0\)
\(c_i = k_i\) kun \(p_i = 0\)
\(c_i = 0\) kun \(k_i = 1\) ja \(p_i = 1\)

Vastaavasti voidaan laskea \(p_i\) tai \(k_i\) arvot.

Yhteenlasku modulo 2 vastaa binäärilukuosiossa käsiteltyä XOR-operaatiota (ehdoton tai).

Yllä esitettyjen yhteen- ja vähennyslaskujen lisäksi voidaan laskea myös kertolaskuja siten, että luvut kerrotaan normaalisti, minkä jälkeen otetaan jakojäännös modulo \(n\). Esimerkiksi \((2 * 4) \pmod{7} = 1\).

Modulo alkuluvuilla¶

Voidaan myös osoittaa, että jakolasku modulo \(n\) on yksiselitteisesti määritelty kaikille luvuille 1:stä \(n-1\) :een, jos \(n\) on alkuluku tai alkuluvun potenssi. Eli silloin kaikille luvuille \(a\) väliltä \([1,n-1]\) on löydettävissä luku \(a^{-1}\) samalta väliltä siten, että \(a * a^{-1} \equiv 1 \pmod{1}\). Esimerkiksi yllä näimme, että luku 4 on luvun 2 käänteisluku modulo 7.

Kun \(n\) on alkuluku tai alkuluvun potenssi, voidaan siis määritellä yhteen-, vähennys-, kerto- ja jakolaskut neutraalialkioineen (0 ja 1) modulo \(n\). Tällöin välillä 0:sta \(n-1\):een olevien kokonaislukujen joukko muodostaa niin sanotun äärellisen kunnan algebrallisen rakenteen, jolla on paljon sovelluskohteita kryptografiassa.

Modulon käyttö kryptografiassa¶

Kategorisesti on yleistettävissä, että tietokoneet laskevat kaikkia laskutoimituksia jossain kunnassa (eli modulon määrittämässä äärellisessä avaruudessa). Siten myös suurin osa tiedon salauksessa käytetyistä menetelmistä toimii myös rajoitetussa numeroavaruudessa. Moderneissa salausmenetelmissä käsitellään usein modulolaskentaa huomattavasti suuremmilla luvuilla, modulo voi olla esimerkiksi alkuluku

\[n = 57896044618658097711785492504343953926634992332820282019728792003956564819949 = 2^{255}-19\]

Yksi esimerkki tästä löytyy tällä hetkellä maailman eniten käytetyn salausmenetelmän AES:n sisäisestä rakenteesta. Keskeisessä roolissa AES:ssä on niin sanottu S-box, joka perustuu suomalaisen emerita professori Kaisa Nybergin kehittämään rakenteeseen, jossa lasketaan bitti-käänteisluku moduloon \(n=256\). Tosin AES:n tapauksessa tekniset yksityiskohdat käänteisluvun laskennassa hieman poikkeavat yllä esitetystä, mutta idea on silti sama. Tähän palataan myöhemmin kurssin aikana.

Yhteenveto¶

Moduloaritmetiikka on keskeinen matematiikassa, kryptografiassa sekä yleisesti ottaen tietojenkäsittelyssä. Tämän moduloaritmetiikan johdannon jälkeen käytämme modulolaskentaa lähes kaikissa esimerkeissämme.