Substituutio ja transpositio¶

Substituutio¶

Substituutio on matemaattinen käsite ja algoritmi, jota käytetään kryptografisissa salaimissa. Substituutiolla korvataan lähtöjoukon alkioita maalijoukon alkioilla. Alkio on tietokoneen tapauksessa tietty määrä bittejä, joita voidaan tulkita kirjaimina, numeroina tai muuna digitaalisena informaationa. Tässä opetusmoduulissa, käsitellessämme historiallisia salaimia, elementit ovat aakkosia.

Koska tietokone käsittelee aakkoset bitteinä tai tavuina, myös salaimissa substituutio suoritetaan luonnollisesti bitteinä ja tavuina. Historiallisissa salaimissa esimerkkeinä alkiosta käytetään aakkosten kirjainta, jolloin tiedon salaus voidaan toteuttaa suoraan substituutiona eli vaihtamalla kirjain toiseksi. Historialliset salaimet ovat siis erikoistapaus substituution käytössä.

Määritellään substituution käsitteet matematiikan avulla seuraavasti:

Lähtöjoukko pitää sisällään korvattavat alkiot.
Maalijoukko pitää sisällään alkiot, joilla korvaus suoritetaan.
Substituutio on funktio, joka kuvaa miten lähtöjoukon alkio korvataan maalijoukon alkiolla.
Injektiivisuus: kuhunkin maalijoukon alkioon kuvautuu vain yksi lähtöjoukon alkio.
Surjektiivisuus: jokaiseen maalijoukon alkioon kuvautuu lähtöjoukon alkio.
Bijektiivisuus: funktio, kun sen kuvaus on sekä injektiivinen että surjektiivinen
Alkukuva: Lähtöjoukosta muodostetut mahdolliset yhdistelmät. Jos esimerkiksi lähtöjoukko sisältää aakkoset A:sta Ö:hön, voisi alkukuva olla vaikka sana ”KISSA”.

Esimerkki¶

Katsotaan edellisiä käsitteitä esimerkin avulla, jossa lähtö- ja maalijoukkojen alkiot eivät ole samoja. Substituution funktio $f$ määrittää, miten lähtöjoukon alkio kuvautuu maalijoukkoon. Alla funktion suorittama substituutio on määritelty alkioittain:

Lähtöjoukko sisältää alkiot A, B ja C.
Maalijoukko sisältää alkiot D, E ja F.
Substituutio on funktio $f$. $f$ kuvaa lähtöjoukon A:n D:ksi, B:n E:ksi ja C:n F:ksi. Käänteinen funktio $f^{-1}$ kuvaa D:n A:ksi, E:n B:ksi ja F:n C:ksi.

Tämä kuvaus lähtöjoukosta maalijoukkoon on bijektiivinen. Seuraava kuva havainnollistaa substituutio-funktiota $f\colon\{A,B,C\}\rightarrow\{D,E,F\}$.

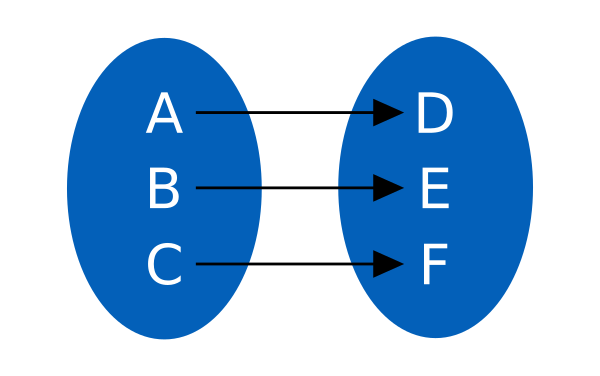
Vastaavasti käänteisfunktio kuvaisi käänteisesti alkiot, eli $f^{-1}\colon\{D,E,F\}\rightarrow\{A,B,C\}$. Edellisen esimerkin substituutio voidaan myös esittää yksinkertaisella taulukolla. Taulukkoon asetetaan allekkain selväkielisen tekstin lähtöjoukon kaikki merkit ja salatekstin maalijoukon korvaavat merkit. Seuraava taulukko esittää saman substituution $\{A,B,C\} \rightarrow \{D,E,F\}$ kuin aiempi kuva.

Joukko	Korvaus 1	Korvaus 2	Korvaus 3
selväteksti	A	B	C
salateksti	D	E	F

Historiallisten salainten kuvausfunktio¶

Historiallisten salainten tapauksessa käsittelemme esimerkeissämme luonnollista tekstiä, joka muodostuu aakkosista. Nyt esimerkkimme on varsin yksinkertainen, mutta myöhemmin lähtöjoukon ja maalijoukon hahmottaminen ei ole näin helppoa. Historiallisten salainten yhteydessä määritämme seuraavasti:

Lähtöjoukon alkiot ovat suomen aakkoset $\{A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z,Å,Ä,Ö\}$.
Maalijoukon alkiot ovat suomen aakkoset $\{A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z,Å,Ä,Ö\}$.
Substituutio on funktio, joka toimii eri tavoin jokaisen kolmen historiallisen salaimen esimerkissä.
Alkukuvia ovat ne lähtöjoukon yhdistelmät, joista funktio pystyy kuvaamaan maalijoukon ryhmän.

Näemme, että luonnollisen kielen tapauksessa sekä lähtö- että maalijoukko muodostuvat samoista aakkosista. Lähtö- ja maalijoukot eivät kuitenkaan välttämättä ole samat. Meillä voi esimerkiksi olla olemassa salain, jossa:

Lähtöjoukko on $\{A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z,Å,Ä,Ö\}$.
Ja maalijoukko on $\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,A,B,?,=,\&,\%,\$,€,\#,§\}$.

Tietokoneen käsittämä lähtö- ja maalijoukko koostuvat tietyn mittaisista bittikuvioista, esimerkiksi 8-bittisistä tai 128-bittisistä ”aakkosmerkeistä”. Ensimmäisessä tapauksessa tietokoneen näkemä ”aakkosto” sisältää $2^8 = 256$ merkkiä ja toisessa on jo $2^{128}$ merkkiä.

Tämän lisäksi on olemassa salaimia, joista pieni lähtöjoukon ”aakkosto” kuvautuu huomattavasti laajempaan maalijoukkoon (katso lisää aiheesta: Classic McEliece https://classic.mceliece.org/). Emme käsittele koodipohjaisia salaimia kurssilla, vaikka niillä on rooli esimerkiksi kvantti-turvallisessa kryptografiassa.

Palataan takaisin yksinkertaiseen esimerkkiimme, jossa lähtö- ja maalijoukko koostuvat suomen kielen aakkosista. Matemaattinen tapa esittää substituutio on käyttää funktioita ja joukkoja. Tämä muistuttaa aiemmin opittua merkintää $f(x) = y$, jossa funktio $f$ kuvaa esimerkiksi reaaliluvun $x$ reaaliluvuksi $y$. Tällöin sanomme, että $x$ ja $y$ kuuluvat reaalilukujen joukkoon $x,y \in \mathbb{R}$ ja funktio $f$ kuvaa reaaliluvun $x$ reaaliluvuksi $y$ eli $f\colon \mathbb{R} \to \mathbb{R}$. Kryptografiassa reaalilukujen $\mathbb{R}$ sijasta käytämme usein kokonaislukuja $\mathbb{Z}$.

Tässä opetusmoduulissa esiteltävissä historiallisissa salaimissa lähtöjoukon muodostavat aakkoset A:sta Ö:hön, joita indeksoimme luvuilla nollasta 28:aan. Substituutiofunktio käyttää laskennassa aakkosten indeksejä. Indeksit alkavat nollasta, eli indeksi 0 = A, indeksi 1 = B ja niin edelleen.

indeksi	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28
alkio	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z	Å	Ä	Ö

Tekstin esikäsittely¶

Luonnollinen teksti esikäsitellään siten, että pienet kirjaimet muunnetaan suuriksi kirjaimiksi ja välimerkit poistetaan. Tällöin lähtö- ja maalijoukon elementit ovat suomen aakkosia $\{A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z,Å,Ä,Ö\}$.

Historiallisissa salaimissa tämä on vakiintunut tapa esikäsitellä viestit. Oletetaan, että Alice haluaa lähettää Bobille seuraavan viestin:

Kahvi Charlotassa on hyvää ja vahvaa!

Jos viesti tässä muodossa salattaisiin seuraavassa osiossa esiteltävällä Atbash-korvaussalaimella, tuloksena olisi seuraava salateksti:

Sövhu Åvölrojökkö op vehbb tö hövhöö!.

Tässä muodossa salateksti paljastaa tietoa lauseesta ja sanoista.

Ensinnäkin siitä pystyy arvaamaan milloin lause alkaa, koska ensimmäinen merkki on iso kirjain.
Toiseksi on pääteltävissä, että seuraava sana on mitä luultavimmin erisnimi tai muu isolla alkukirjaimella kirjoitettava sana.
Kolmanneksi esikäsittelemättömästä salatekstistä näkee myös sen, että siinä on käytetty kahta kaksikirjaimista sanaa ’op’ sekä ’tö’. Näitä sanoja on suomen kielessä vain muutama. Sitten kun tunnemme Atbash-salaimen toiminnan, voimme päätellä että Atbash-muunnos suomen lähtö- ja maalijoukolla tarkoittaa sitä, että selväkielen ’O’-kirjain kuvautuu salakielen ’O’-kirjaimeksi. Tämä yhdistettynä suomen kielen harvaan kaksikirjaimisten sanojen listaan auttaa arvaamaan, että ’P’-kirjain on todennäköisesti joko ’N’- tai ’K’-kirjain.

Historiallisissa salaimissa selväkielinen teksti esikäsitellään ensin merkkijonomuotoon. Tällöin sanoja ei helposti pysty erottamaan salatekstistä. Esikäsittelyssä suoritetaan seuraavat operaatiot:

kaikki viestin kirjaimet muunnetaan isoiksi kirjaimiksi ’a’-> ’A’ … ’ö’->’Ö’
kaikki välilyönnit, välimerkit ja numerot poistetaan

Näin selväteksti:

Kahvi Charlotassa on hyvää ja vahvaa!

esikäsitellään selväkieliseksi merkkijonoksi:

KAHVICHARLOTASSAONHYVÄÄJAVAHVAA.

Jolloin Atbash-salattuna esikäsitelty viesti muuttuu salakirjoitukseksi:

SÖVHUÅVÖLROJÖKKÖOPVEHBBTÖHÖVHÖÖ.

Nyt salateksti antaa huomattavasti vähemmän vihjeitä sanoista, sanaväleistä, erisnimistä ja lauserakenteesta. Toinen syy merkkijonomuunnokselle on se, että salaus ja salauksen purku, eli enkryptaus- ja dekryptausoperaatiot, on helpompi toteuttaa myös käsin. Seuraavassa koodisolussa voit kokeilla itse viestin esikäsittelyä.

Inactive

# käytetään kirjasto-funktioita
from xip import merkistot, esikasittele_teksti

# Haetaan suomen aakkoset
isot, pienet = merkistot(suomi=True)

# Voit muuttaa tätä viestiä ja kokeilla, miten esikäsittely toimii
viesti = "Kahvi Charlotassa on hyvää ja vahvaa!"

# Tulostetaan viesti ja esikäsitelty viesti
print("Viesti on              :", viesti)
print("Esikäsitelty viesti on :", esikasittele_teksti(viesti, isot+pienet))

Transpositio¶

Transpositio on toinen salaimissa käytössä oleva perusoperaatio. Transpositiossa viestin merkkien paikat sekoitetaan. Merkkejä ei siis korvata toisilla merkeillä kuten substituutiossa.

Otetaan esimerkiksi viesti ”HEIBOB”.

Numeroidaan jokainen kirjain indeksillä, jolloin H:lla on indeksi 0 ja viimeisenä olevalla B-kirjaimella indeksi 5.
Ensimmäinen transpositiofunktio lisää jokaiseen indeksiin +1.
Indeksiä rajoitetaan siten, että jos käyttämämme indeksi menee yli viiden, se palaa nollaan. Tämä on ensimmäinen moduloaritmetiikan esimerkki, jossa toteutamme modulo 6 laskennan.
Tämän jälkeen järjestetään kirjaimet muutetun indeksin mukaisesti nollasta viiteen.

Alla esimerkki +1 transpositiosta (modulo 6).

Alkuperäinen
selväkirjoitus	H	E	I	B	O	B
indeksi	0	1	2	3	4	5

Indeksi+1
selväkirjoitus	H	E	I	B	O	B
indeksi	1	2	3	4	5	6

Modulo 6
selväkirjoitus	H	E	I	B	O	B
indeksi	1	2	3	4	5	0

Järjestetty
salakirjoitus	B	H	E	I	B	O
indeksi	0	1	2	3	4	5

Viesti on yhä kohtuullisen helppo tulkita. Tämä johtuu siitä, että viesti on lyhyt ja käytännössä vain ”tökkäsimme” kirjainjonoa yhdellä pykälällä ”oikealle”. Näin käytännössä vain viimeinen kirjain siirtyi ensimmäisen kirjaimen paikalle.

Transposition esimerkki permutoimalla¶

Käytämme permutointia silloin, kun haluamme selvittää kuinka monella tavalla voimme järjestää viestin merkit, tai esimerkiksi sanan kirjaimet, eri järjestykseen. Jos otetaan sana ”MOI”, voimme järjestää tuon sanan kirjaimet kuudella eri tavalla: ’MOI’, ’MIO’, ’OMI’, ’OIM’, ’IMO’, ’IOM’.

Luodaan toinen viesti ”TÄTI” ja käytetään Python-kirjastoa tutkiaksemme, miten permutaatiot voi tuottaa. Huomaat seuraavassa esimerkissä, että jotkin permutaatioista ovat kirjaimiltaan samoja. Jos vaihtaa T-kirjainten paikkaa, teksti ei muutu vaikka kyseessä ovat teknisesti eri permutaatiot. Itse permutaatioita mielenkiintoisempaa on permutaatioilla saavutettava ainutlaatuisten (engl. unique) permutaatioiden lukumäärä.

Tarkastellaan permutaatioiden lisäksi sitä, kuinka monta yksilöllisiä permutaatiota ”TÄTI”-viestistä on mahdollista tuottaa. Tämä tapahtuu Python-kielellä luomalla annetuista vaihtoehdoista joukko (engl. set).

Inactive

from itertools import permutations

# Kokeillaan miten monta tapaa on permutoida viesti TÄTI
viesti   = "TÄTI"              # luodaan lyhyt viesti
permutaatiot = [''.join(p) for p in permutations(viesti)]

print("Kaikkia permutaatiota on:",len(permutaatiot))
# Tulostetaan kaikki permutaatiovaihtoehdot
print("Kaikki", viesti," permutaatiot:", permutaatiot)

# Muodostetaan kaikista permutaatioista joukko ja tulostetaan tuon joukon koko.
print("\n\nYksilöllisiä MOII permutaatiota on", str(len(set(permutaatiot))))
# Tulostetaan yksilölliset permutaatiot
print("Yksilölliset permutaatiot:", set(permutaatiot))

Pitkän viestin permutaatiot¶

Jos käytämme samaa viestiä kuin substituutioesimerkissä: ”KAHVICHARLOTASSAONHYVÄÄJAVAHVAA”, niin kuinka monella tapaa voimme järjestää kirjaimet?

indeksi	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
alkio	K	A	H	V	I	C	H	A	R	L	O	T	A	S	S	A	O	N	H	Y	V	Ä	Ä	J	A	V	A	H	V	A	A

Näitä permutaatioita on hyvin paljon ja yleensä permutaation tuloksesta halutaan sellainen, että se hajauttaa kirjaimet mahdollisimman tehokkaasti. Kuinka monella tapaa voimme järjestää esimerkkinä käytetyn 31 kirjainta pitkän viestin? Lasketaan:

Ensimmäinen merkki voi saada minkä tahansa 31:stä indeksinumerosta.
Toinen merkki voi saada minkä tahansa jäljelle jäävistä 30:stä indeksinumeroista.
Jokaiselle merkille annetaan indeksi, kunnes kaikki indeksinumerot 0..30 on käytetty.

Tässä vaiheessa esitellään matematiikan käsite kertoma, jota merkitään huutomerkillä (!).

Näin kertoma (!) lasketaan:

0! = 1
1! = 1
2! = 1 x 2 = 2
3! = 1 x 2 x 3 = 6
4! = 1 x 2 x 3 x 4 = 24
…
N! = 1 x 2 x … x (N-1) x N

Formaalisti määritämme kertoman seuraavasti luvulle $n$ :

$n! = n\cdot(n-1)\cdot(n-2)\dotsm 3 \cdot 2 \cdot 1$

Näin ensimmäisen merkin indeksinumerolle on 31 vaihtoehtoa, toiselle 30, kolmannelle 29 jne. Eli tapoja, joilla indeksit voi järjestää eli permutoida on luvun 31 kertoman (!) verran eli $31\mathbf{!}\,=31\times30\times29\times...\times1$.

Jos viesti on ”KAHVICHARLOTASSAONHYVÄÄJAVAHVAA”, kaikkien mahdollisten permutaatioiden tuottaminen kestää aivan liian kauan. Alla oleva funktio laskee permutaatioiden lukumäärän hyödyntämällä kertomaa ja palauttaa yhden satunnaisen permutaation tuloksen.

Inactive

from itertools import permutations

from xip import näytä_permutaatiot
viesti = "KAHVICHARLOTASSAONHYVÄÄJAVAHVAA"
näytä_permutaatiot(viesti)

Yhteenveto¶

Tässä osiossa olemme oppineet, miten substituutio ja permutaatio (eli transpositio) toimivat Näitä operaatioita käytetään laajasti salaimissa.

Ymmärrämme nyt myös, miksi luonnollisen kielen tekstiä on hyvä esikäsitellä.

Transposition yhteydessä käytimme moduloaritmetiikkaa. Moduloaritmetiikkaa käytetään kaikissa tulevissa menetelmissämme. Seuraava luku keskittyykin tähän aiheeseen.