Kurssin viimeisimmän version löydät täältä: Johdatus kryptografiaan: 2024
Kryptografian elementit ja luottamuksellisuus¶
Kryptografialla salataan ja suojataan informaatiota. Kurssillamme informaatiota voi olla mikä tahansa digitaalinen data. Käytämme konkreettisena salattavana ja suojattavana informaationa viestiä.
Viestin salaamisessa pyritään takaamaan viestin luottamuksellisuus. Salatessamme viestin sisältöä käytämme kryptografiassa käsitteitä selväkieli, salakieli, salain ja avain.
Salain on menetelmä, algoritmi tai laite, joka käyttää avainta muuttaessaan selväkielen salakieleksi tai salakielen selväkieleksi. Käytettävät algorimit ovat enkryptaus, joka salaa viesti salakieleksi, sekä dekryptaus, joka purkaa viestin selväkielelle. Alla tutustumme jokaiseen näistä elementeistä tarkemmin.
Selväkieli tarkoittaa mitä tahansa salaamatonta tietosisältöä. Selväkieltä merkitään symbolilla \(\textbf{P}\) matemaattisissa yhtälöissä. Kirjallisuudessa esitellään kaksi englanninkielistä käsitettä plaintext ja cleartext, jotka kummatkin tulkitaan suomessa selväkieleksi.
Englannin käsite plaintext tarkoittaa salaamatonta viestiä, joka ei välttämättä ole sellaisenaan ihmisymmärrettävässä muodossa.
Plaintext voi olla esimerkiksi binääriä dataa kuten vaikka 128-bittinen AES avain.
Kuten näimme jo esittelyluvussa Bitit, tavut ja binäärioperaatiot, bitit voidaan esittää heksadesimaalimuodossa,
jolloin 128-bittiä näyttäisi esimerkiksi heksadesimaalisena seuraavalta: 0x5E2FA74A7A16E87BD64A770BD8FB76E8.
Tällä tavalla esitetyssä muodossa avain on salaamaton,
mutta sitä tarkastelevalle ihmiselle sen sisältö ei sellaisenaan ole tulkittavissa olevaa tietoa.
Avain, joka tässä näytetään selväkielenä, on tiedon salauksen ja suojauksen kannalta tärkein salattava tieto.
Toinen englanninkielinen käsite, cleartext, on myös salaamaton viesti. Cleartext on muodossa, jota ihminen kykenee tulkitsemaan. Esimerkiksi viesti ”Muista kastella kukat!” on esimerkki ihmisen ymmärtämästä selväkielestä.
Esimerkki selväkielestä: merkistökoodaus¶
Käytämme harjoituksissa ajoittain tekstidokumentteja, jotka ovat yksi esimerkki selväkielisestä viestistä. Esimerkkeinä käytetään tekstejä, koska niillä on helppo esittää ero selväkirjoituksen ja salakirjoituksen välillä.
Tietokone ei näe kirjaimia sellaisenaan, vaan tallentaa aakkosten merkit biteiksi ja tavuiksi eli ykkösten ja nollien jonoiksi. Jos aihe tuntuu etäiseltä, voit kerrata bittien ja tavujen perusteita edellisessä opetusmoduulissa.
Tietokoneen ymmärtämien bittikuvioiden tulkitsemiseen ja muuntamiseen ihmisen
ymmärtämään muotoon on olemassa yleisesti käytössä oleva standardimuotoinen tapa.
Tällä tavalla voimme esimerkiksi tulkita, että bittikuvio 0b11000100 vastaa aakkosten kirjainta Ä.
Tällaiset merkistökoodaukset eivät ole kryptografiaa,
vaan yhdessä sovittu tapa tallentaa ja muuntaa ihmisten tuottama informaatio digitaaliseen muotoon.
Merkistökoodattu teksti ei siis ole salattua, vaan se on selväkieltä.
Myöskään aiemmin mainittu bittikuvio ei ole salattua informaatiota.
Se on selväkieltä, vaikka emme pystykään helposti ymmärtämään sitä.
Seuraava kuva näyttää perinteisen 7-bittisen ASCII-taulukon.
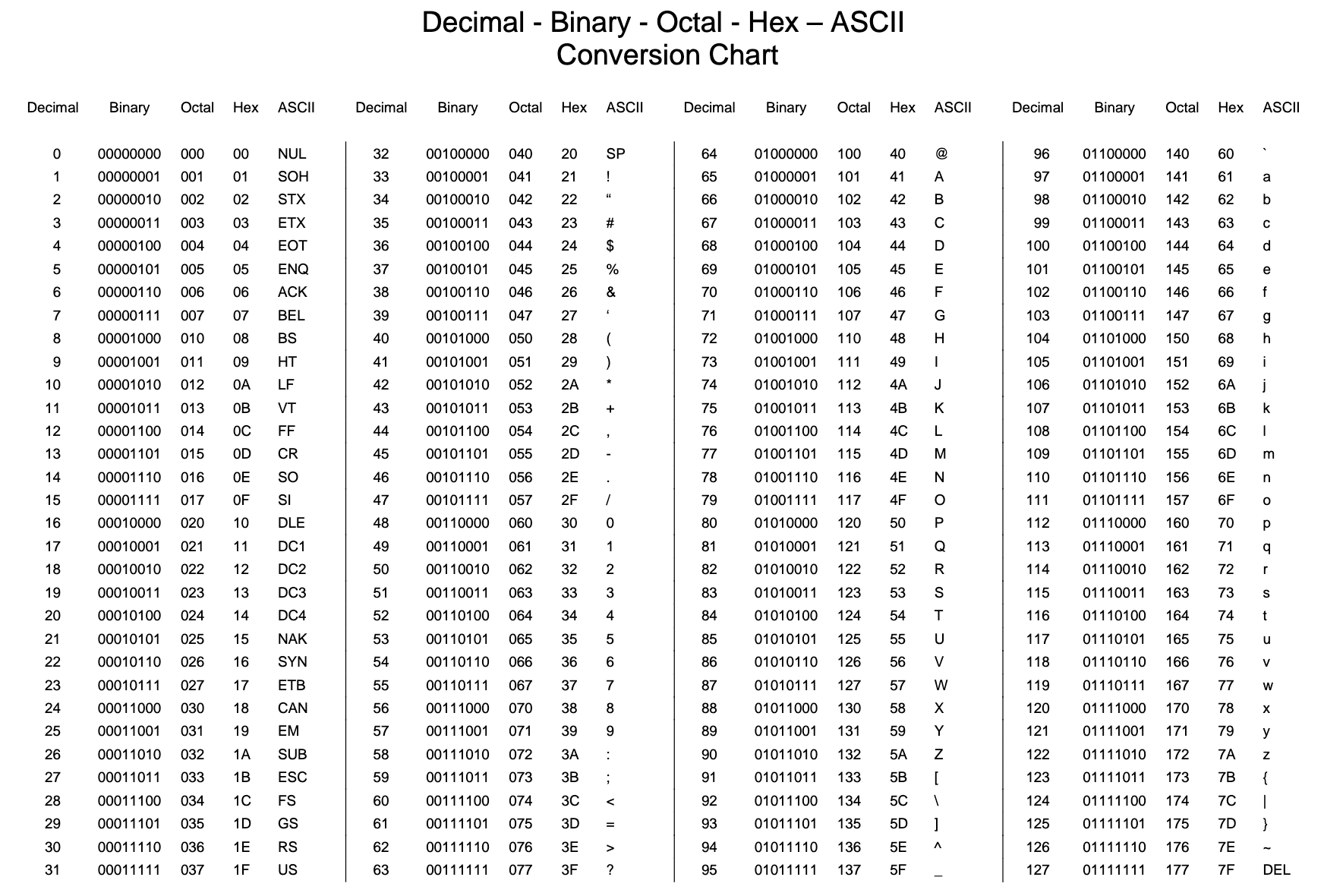
Lähde: ascii-taulu¶
Huomasitko, että Ä-kirjain puuttuu taulukosta? Kohtaat tämän kurssin harjoituksissa melko varmasti merkistökoodaukset Unicode ja UTF-8. Python käsittelee suomen kielen merkistöt esimerkiksi UTF-8-, Unicode- tai latin_1-koodattuna. Merkistökoodaukset ovat kokonaan oma maailmansa, eivätkä ne liity kryptografiaan.
Tarvitset oheista koodia vastataksesi alla oleviin kysymyksiin.
from numpy import binary_repr
kirjain = u'Ä' # Vaihda tähän hipsujen sisään haluamasi kirjain esim A, a, Ä
muoto = 8 if ord(kirjain)< 255 else 32
print("Kirjain: {} desimaalinumero: {:3d} hexadesimaali: {} bitteinä :b'{}".format(kirjain, ord(kirjain), hex(ord(kirjain)), binary_repr(ord(kirjain), muoto)))
Toinen tehtävä:

Kryptografian ytimessä on salain, englanniksi cipher. Salainta merkitään matemaattisissa kaavoissa useilla eri symboleilla riippuen siitä, mihin salainta käytetään.
Enkryptaus: Salaimella tuotetaan selväkielestä salakieltä. Tällöin matematiikan yhtälöissä käytetään yleensä symbolia \(\textbf{E}\). Usein puhutaan salauksesta, vaikka nimitys on jossain määrin harhaanjohtava. Salaus on kyseessä silloin, kun tavoitellaan jonkun informaation luottamuksellisuutta salaamalla sisältö. Käytämme kurssilla myös satunnaisesti puhekielistä termiä enkryptio, koska termi toimii hyvin myös autenttisuuden ja eheyden yhteydessä.
Dekryptaus: Salaimella tuotetaan salakielestä selväkieltä. Tällöin matematiikan yhtälöissä käytetään yleensä symbolia \(\textbf{D}\). Tällä kurssilla käytämme myös puhekielistä termiä dekryptio, koska termi toimii hyvin myös autenttisuuden ja eheyden yhteydessä.
Yksi hyvän salaimen tunnusmerkki on, että salain tuottaa salakieltä jonka sisältö muistuttaa satunnaista kohinaa. Kryptografinen salain pyrkii tuottamaan informaatiolle tarvittavan luottamuksellisuuden, autenttisuuden ja eheyden.
Salain ilman avainta¶
Osa historiallisista salaimista perustui salaimen toiminnan salaamiseen. Tällaisissa salaimissa ei välttämättä käytetty erillistä avainta, joka kontrolloisi salaimen toimintaa. Voisimme myös väittää, että tällainen salain pitää sisällään myös avaimen.
Yksi esimerkki historiallisesta avaimettomasta salaimesta on spartalaisten sotavoimien käyttämä ”skytale”-keppi. Tämä menetelmä on hyvä esimerkki transpositiosalauksesta, jota käsittelemme myöhemmässä opetusmoduulissa.

Skytale-kepin paksuus ja mahdollisesti sen muoto määrittivät, kuinka kepin ympärille kääritty ohut pergamenttinauha asettui. Viesti kirjoitettiin kepin suuntaisesti kepin ympärille sidotulle nauhalle, ja kun nauha avattiin kepin ympäriltä, näytti kuin ohut pergamenttiliuska olisi sisältänyt kirjaimia satunnaisessa järjestyksessä. Kirjaimet eivät siis muuttuneet toisiksi kirjaimiksi, mutta vaihtoivat paikkaa.
Viestin vastaanottajalle välitettiin pergamentti sekä tieto käytetyn Skytale-kepin mitoista. Vastaanottaja purki viestin käärimällä pergamentin samanlaisen Skytale-kepin ympärille. Jos ulkopuolinen taho olisi saanut haltuunsa viestin sekä selvittänyt käytetyn skytale-kepin mitat, olisi hän pystynyt tulkitsemaan viestin sisällön.
Salain avaimella¶
Historiallisesti olennainen salausmenetelmä on Julius Caesarin aikoihin käytetty Caesar-salaus. Salauksessa aakkoset kuvitellaan olevan järjestyksessä A:sta Ö:hön (suomeksi) ja latinalaisessa aakkostossa A:sta Z:aan. Eli:
ABCDEFGHIJKLMNOPQRSTUVWXYZÅÄÖ. Latinalaisissa aakkosissa kolme viimeistä merkkiä jäävät pois.
Tehdään seuraavat ajatusleikit:
Haluan korvata kirjaimen X merkillä, joka on kolme (3) askelta ”oikealla”. Tällöin merkki X korvataan merkillä Å.
Haluan korvata kirjaimen Å merkillä, joka on kolme (-3) askelta ”vasemmalla”. Tällöin merkki Å korvataan merkillä X.
Haluan korvata kirjaimen Ä merkillä, joka on kolme (3) askelta ”oikealla”. Tällöin merkki Ä korvataan merkillä B. Merkistön reunan tullessa vastaan Ö-kirjaimen kohdalla, jatkamme laskemista merkistön alkupäästä eli kirjaimesta A.
Haluan korvata kirjaimen B merkillä, joka on kolme (-3) askelta ”vasemmalla”. Tällöin merkki B korvataan merkillä Ä. Merkistön reunan tullessa vastaan A-kirjaimen kohdalla, jatkamme laskemista merkistön loppupäästä kirjaimesta Ö.
Menetelmässä enkryptauksessa selväkielen aakkosten kirjain korvataan toisella kirjaimella, eli kyseessä substituutio. Tällöin merkki korvataan kirjaimella, joka sijaitsee tietyllä etäisyydellä salattavasta kirjaimesta. Voidaan ajatella, että aakkostoa mennään ”oikealle” niin monta askelta kuin avaimen arvo on. Jos oikealle kulkeminen aakkostossa ylittää viimeisen kirjaimen, jatketaan avaimen askelmien laskentaa aakkosten alustaa, aivan kuin A-kirjain olisi seuraavana aakkoston viimeisen merkin jälkeen.
Caesar-salakirjoitus muodostetaan käyttämällä salaimessa kiinteää avainta, eli etäisyyttä jolta korvattava kirjain haetaan. Aiemmin käymässämme ajatusleikissä tämän kiinteä avaimen arvo oli 3.
Näytetään esimerkki oheisen taulukon avulla ja salataan teksti ”HEI” Caesar-salaimella, joka käyttää kiinteää avainta 3.
Selväkielen kirjain |
Avain |
Salakielen kirjain |
|---|---|---|
H |
+3 |
K |
E |
+3 |
H |
I |
+3 |
L |
Vastaavasti Caesar-salauksen dekryptauksessa salakielen kirjain korvataan kirjaimella, joka sijaitsee avaimen arvon etäisyydellä ”vasemmalla” dekryptattavasta kirjaimesta.
Näytetään esimerkki oheisen taulukon avulla ja puretaan teksti ”KHL” Casear-salaimella, joka käyttää kiinteää avainta 3. Tällöin avain voidaan käsittää arvona -3, mikä tarkoittaa että korvaava kirjain löytyy kolmen askeleen päässä ”vasemmalla”.
Selväkielen kirjain |
Avain |
Salakielen kirjain |
|---|---|---|
K |
-3 |
H |
H |
-3 |
E |
L |
-3 |
I |
Seuraavassa luvussa Caesar-salaus, tutustutaan tarkemmin Caesar-salaimeen ihan koodiesimerkkien kautta.
Kerckhoffsin-periaate¶
Osa historiallisista salaimista on käyttänyt avainta, joka on ohjannut salaimen toimintaa tiedon salauksessa ja purkamisessa. Nykyaikaiset salaimet käyttävät lähes poikkeuksetta avainta.
Hollantilainen kielitieteilijä Auguste Kerckhoffs ymmärsi, ettei pelkästään salassa pidettävään algoritmiin perustuva kryptografiajärjestelmä ole luotettava. Hän kirjoitti vapaasti käännettynä: ”Salausjärjestelmän luotettavuus ei saa perustua itse salausjärjestelmän salassapitoon. Vaikka vihamielinen taho saisi järjestelmän haltuunsa, siitä ei saa koitua harmia järjestelmän käytölle.” Nykyiset kryptografiset järjestelmät noudattavat tätä Kerckhoffsin periaatetta. Kerckhoffsin periaate määrittää, että salaimen toiminta, menetelmä ja/tai algoritmit eivät saa olla salaisia. Tällöin salaimen käyttämä avain on ainoa kryptografinen salaisuus.
Tällä kurssilla perehdymme muutaman keskeisen salaimen toimintaperiaatteisiin ja käsittelemme ne matematiikan teoriat, johon salainten toiminta perustuu. Käytännössä salain sisältää matemaattisia operaatioita, joissa avain toimii algoritmin ”ohjekirjana”
Tiedon salauksessa ja suojauksessa käytetty avain on salainen. Avainta merkitään symbolilla \(\textbf{K}\) matemaattisissa yhtälöissä. Avain on salassa pidettävä tieto.
Entisaikojen avaimet saattoivat olla yksittäinen numero, joka tuottaa vakiosiirroksen aakkostoon. Toinen vanha avain on käyttää informaation suojauksessa lausetta kirjasta. Nykyaikana avain on jokin ennalta määrätty määrä satunnaisia bittejä. Käytännössä avain voi muodostua 128:sta tai 256:sta satunnaisesti valitusta bitistä. Myös muita avainpituuksia käytetään, varsinkin kun pääsemme kurssin loppupuolella tarkastelemaan epäsymmetrisiä salaimia.
Yksinkertaisuudessaan avain voi olla esimerkiksi yksittäinen numero, kirjain tai sana. Vastaavasti monimutkainen avain voi esimerkiksi muodostua hyvin suurista alkuluvuista. Myöhemmin kurssilla käytämme erilaisia avaimia hieman erilaisissa rooleissa ja konteksteissa.
On olemassa hyviä avaimia ja huonoja avaimia. Tulemme oppimaan pian, että huonosti valittu avain ei juuri suojaa informaatiota.
Alice ja Bob sopivat, että heidän ensimmäisenä avaimenaan toimii numero 3, samoin kuin klassisessa Caesar-salaimiessa. Jos avainta 3 ei voi käyttää, he sopivat että vaihtoehtoisena avaimena toimii sana OLI. Nämä salaiset avaimet ovat heidän välinen jaettu salaisuus.

Kun selväkielinen viesti salataan salaimen ja avaimen avulla, saamme tulokseksi salakielisen tekstin eli salaviestin. Salakieltä merkitään symbolilla \(\textbf{C}\) matemaattisissa yhtälöissä.
Salaviestin hyvyyttä voi tulkita monin tavoin. Yksi tällainen väite on, että hyvä salakieli näyttää täysin satunnaiselta. Kokeilit jo Caesar-salaimen kanssa kahta eri avainta – näyttikö salakieli täysin satunnaiselta? Tutkimme klassisia salausmentelmiä kolmannessa opetusmoduulissa ja analysoimme salaviestin sisältöä neljännessä opetusmoduulissa.
Kokeillaan salaimia¶
Seuraavassa esimerkissä Alice kokeilee kolmea salainta. Hän luo selvätekstiviestin ”HEIBOB”. Tämä on tapa, jolla voimme olettaa Alicen aloittavan viestinsä Bobille. Selväteksti on siis \(\textbf{P} = \text{"HEIBOB"}\).
Selvätekstiviesti salataan kolmella menetelmällä:
Ensimmäinen salain \(\textbf{E}_a\) ei käytä avainta. Matemaattisesti tämä enkryptaus merkitään: \(\textbf{C}_1 = \textbf{E}_a(\textbf{P})\). Salakieli siis tuotetaan enkryptauksella selväkielestä.
Toinen salain \(\textbf{E}_b\) käyttää avainta 3. Avain on \(\textbf{K}_1 = 3\) ja enkryptaus merkitään matemaattisesti: \(\textbf{C}_2 = \textbf{E}_b(\textbf{K}_1,\textbf{P})\).
Kolmas salain \(\textbf{E}_c\) käyttää avainta \(\textbf{K}_2 = \text{"KISSA"}\). Vastaavasti enkryptaus \(\textbf{C}_3 = \textbf{E}_c(\textbf{K}_2,\textbf{P})\).
Meillä on seuraavat tekijät:
Yksi selväkieli: \(\textbf{P}\)
Kolme salainta: \(\textbf{E}_a\), \(\textbf{E}_b\) ja \(\textbf{E}_c\).
Kaksi avainta: \(\textbf{K}_1\) ja \(\textbf{K}_2\).
Kolme salakieltä: \(\textbf{C}_1\), \(\textbf{C}_2\) ja \(\textbf{C}_3\).
from xip import salain_a, salain_b, salain_c
# Asetetaan viesti muuttujaan P eli plaintext
P = "HEIBOB"
print("Viesti selvätekstinä: {} ".format(P))
# Käytetään salain_a:ta (E_a), tuotetaan C_1
C_1 = salain_a(viesti=P)
print("Salain A tuottaa salakielen {} ilman avainta".format(C_1))
# Käytetään salainta b (E_b), alkuperäinen K_1=4
K_1 = 4 # <- Joudut vaihtamaan tätä avainta harjoituksessa.
C_2 = salain_b(viesti=P, avain=K_1)
print("Salain B tuottaa salakielen {} avaimella {}".format(C_2, K_1))
# Käytetään salainta c (E_c), alkuperäinen K_2="KISSA"
K_2 = "KISSA" # <- Joudut vaihtamaan tätä avainta harjoituksessa
C_3 = salain_c(viesti=P, avain=K_2)
print("Salain C tuottaa salakielen {} avaimella {}".format(C_3, K_2))
Seuraavaan tehtävään joudut vaihtamaan avainta.
Yhteenveto¶
Yhteenveto juuri oppimistamme asioista:
Selväkieli on tulkittavissa olevaa tietoa. Sen symboli on \(\textbf{P}\).
Salaimella on kaksi toimintaa: enkryptaus \(\textbf{E}\) ja dekryptaus \(\textbf{D}\).
Salaimen käyttämä avain on salaisuus. Avaimen symboli on \(\textbf{K}\).
Salakieli \(\textbf{C}\) tuotetaan salaimella selväkielestä: \(\textbf{C} = \textbf{E}(\textbf{K},\textbf{P})\).
Selväkieli \(\textbf{P}\) voidaan tuottaa salaimella salakielestä: \(\textbf{P} = \textbf{D}(\textbf{K},\textbf{C})\).
Käytimme esimerkeissä kolmea salainta, kahta avainta ja tuotimme kolme salatekstiä.
Kryptografiassa on tunnettava, millaisia hyökkäyksiä vastaan tietoa salataan ja suojataan. Seuraavaksi tutustumme hyökkäysmalleihin, joiden tunteminen on välttämätöntä suunnitellessamme ja käyttäessämme kryptografian menetelmiä.